AP Precalculus Unit 1b

BOBO

Bigger on bottom | y = 0

BOTN

Bigger on top | No horizontal asymptote.

EATS DC

Exponents are the same, divide coefficients | y = a/b

BOBO (explanation in words)

If the leading coefficient in the denominator is greater than the numerator the horizontal asymptote lies where y = 0.

BOTN (explanation in words)

If the leading coefficient in the numerator is greater than the denominator then there is no horizontal asymptote.

BOBO limit statement

lim x → ∞ f(x) = 0
lim x → −∞ f(x) = 0

EATS DC limit statement

lim x → ∞ f(x) = a/b

lim x → −∞ f(x) = a/b

BOTN limit statement

lim x → ∞ f(x) = ∞

lim x → −∞ f(x) = −∞

WORK OUT PAGE 26

AP NOTES #7

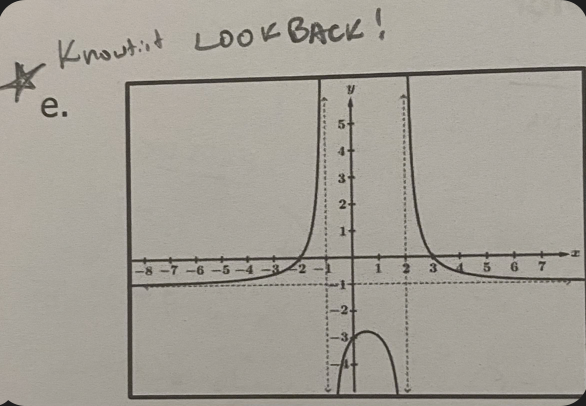
Write a limit statement

lim x → ∞ f(x) = -1

lim x → −∞ f(x) = -1

When do we have a slant asymptote?

When the degree of the numerator is one greater than the degree of the denominator

Slant Asymptote: Limit statement: a/b > 0

lim x → ∞ f(x) = ∞

lim x → −∞ f(x) = −∞

Slant Asymptote: Limit statement: a/b > 0

lim x → ∞ f(x) = −∞

lim x → −∞ f(x) = ∞

where is a root?

numerator term = 0

where are asymptotes?

denominator term = 0

roots

[, ]

asymptotes

(, )

WORK OUT PAGE 29

AP NOTES #8

< 0 

only (,)

< 0

both (,) and [,]

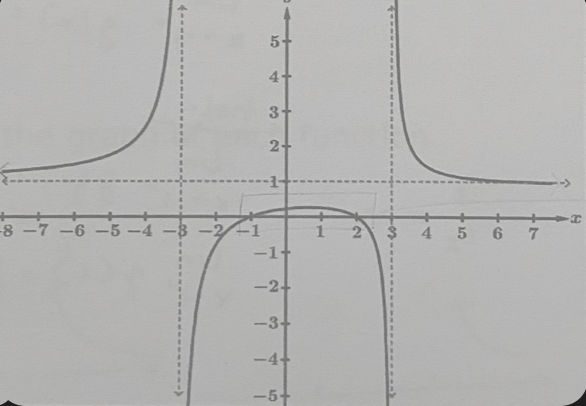
a. f(x) < 0

(-3,-1] [2,3)

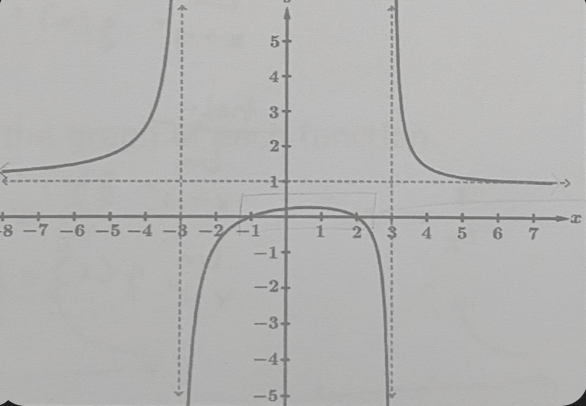
b. f(x) > 0

(−∞,-3) (-1,2) (3,∞)

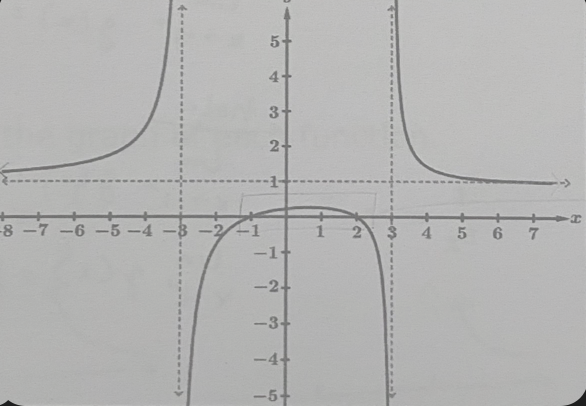
c. f(x) > 0

(−∞,-3) [-1,2] (3,∞)

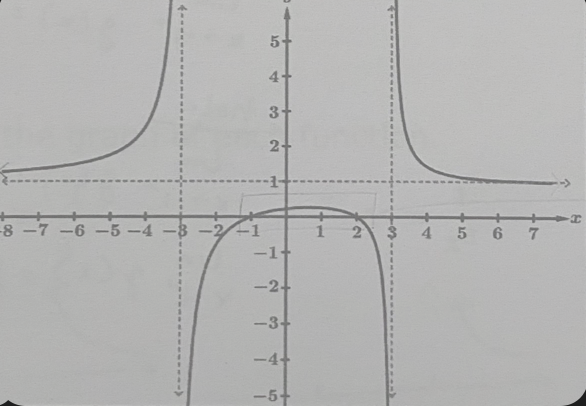
f(x) > 1

(−∞,-3) (3,∞)

Find the equation g(x)

Identify the VA, write corresponding limit statements

Identify the Hole, write the corresponding limit statements

Equation: g(x) = 2(x-1)(x+2)/(x-1)(x+1)

VA: x = -1

lim x → -1^- g(x) = −∞

lim x → -1^+ g(x) = ∞

Hole: (1,3)

lim x → -1^- g(x) = 3

lim x → -1^+ g(x) = 3

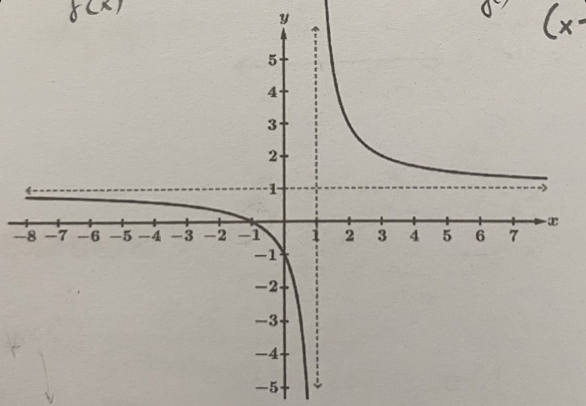
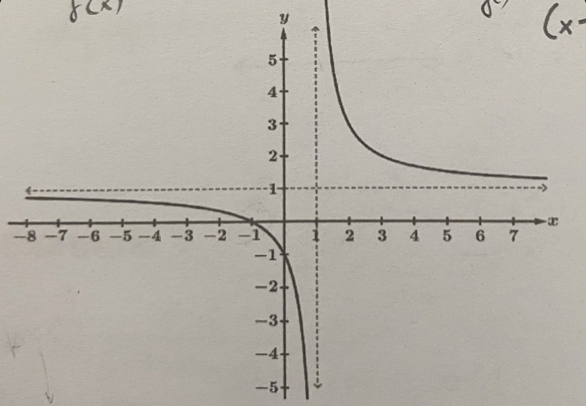
Find the equation f(x)

Identify the VA, write corresponding limit statements

Identify HA, write the corresponding limit statements

Equation: f(x) = (x+1)/(x-1)

VA: x = 1

lim x → -1^- f(x) = −∞

lim x → -1^+ f(x) = ∞

HA: y = 1

lim x → ∞ f(x) = 1

lim x → −∞ f(x) = 1

Write equations using a limit statement.

lim x→3^- f(x) = 5           lim x→3^+ f(x) = 5

lim x→1^- f(x) = −∞        lim x→1^+ = ∞

10(x-3)/(x-3)(x-1)

Write equations using a limit statement.

lim x→-2^- f(x) = 4         lim x→-2^+ f(x) = 4

lim x→-1^- f(x) = ∞        lim x→-1^+ = ∞

4(x+2)/(x+2)(x+1)²

HW #9

ON DELTA MATH

The multiplicity of an asymptote tells you what on a graph?

The arrow direction

Vertical Translation

g(x) = f(x) + k

Horizontal Translation

g(x) = f(x+h); remember -h units

Vertical Dilation

g(x) = af(x)

Horizontal Dilation

g(x) = f(bx); remember a dilation by 2 multiply the y co-od by ½ | if it were ½ multiply the y co-od by 2.

Reflection

if a < 0 reflection over x-axis

if b < 0 reflection over y-axis