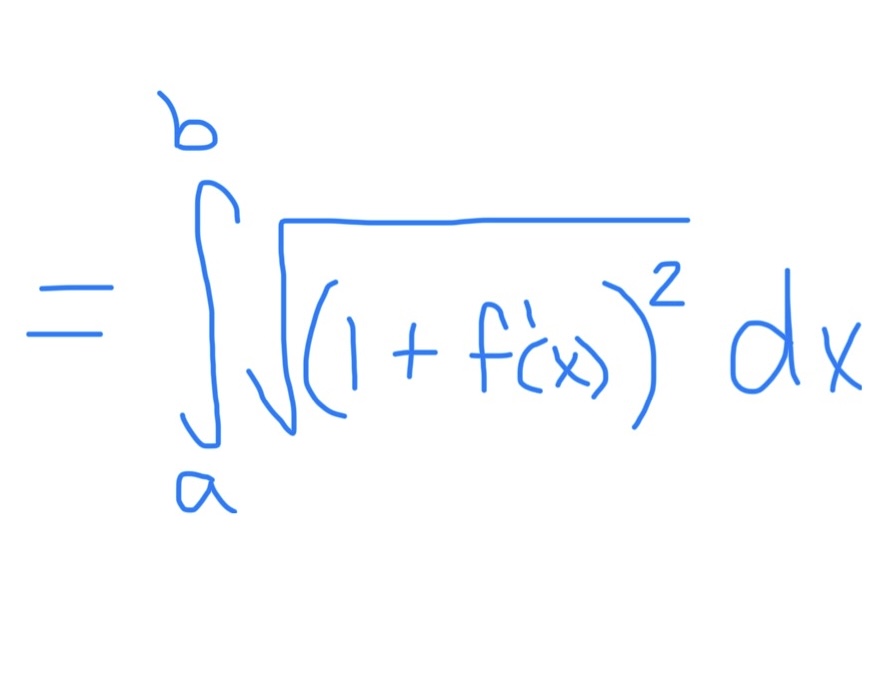Calc II Final Review

Identify the P-Series

n^# or sqrtn

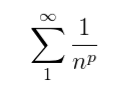
Identify the Geometric Series

r is directly to power of n/k

a is what’s not attached

#ⁿ

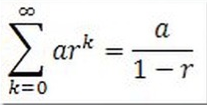
Solving P-Series

1. Identify P aka the power that n/k is to

   • for multiple of them, P is the sum

2. Compare P to 1

   • Absolutely Converges if P is greater than 1

   • Diverges if P is less than or equal to 1

Solving Geometric Series

1. Identify r aka the # that is to the power of k/n

   • if in denominator, only take the value of what is directly attached to k/n, but remember if its a fraction or not being in the denominator

   • if # is to like 2n, keep the power of 2 in r

2. Ask: Is |r| < 1?

   • Yes → Absolutely Converges to s= a/1-r

     • to find a, plug in number n is = to in sigma

   • No → Diverges

To get rid of square roots…

Multiply by the conjugate and use (A-B) (A+B) = A²-B²

Identify Telescoping Series

Terms subtract and when expanded, cancel out only leaving first and last term

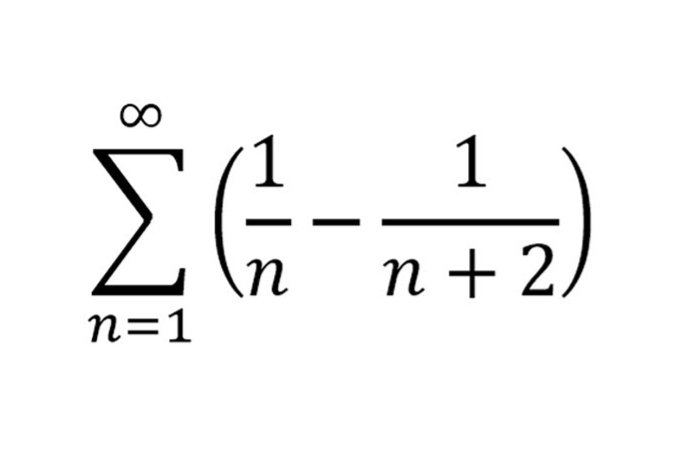
Solving Telescoping Series

1. Expand the series

   • last term is just the second value from the original series but with n’s

2. Cancel out terms except first and last which will be combined

3. Take the limit of this

   • this is the sequence of partial sums

4. If it converges, then so does the series

5. If it diverges, then so does the series

Identifying Almost P-Series

if k^# or sqrtk is added/subtracted by another # or variable (s)

Identifying Almost Geometric Series

if #^k is added/subtracted by another # or variable

Solving Almost Series

1. Determine if almost p-series or geo series

2. Take away lower degree terms to make look alike series Σ bn

3. State “Compare to [insert Σ bn]

4. Decide if using Limit Comparison Test or Direct Comparison Test

5. State the test

6. Perform the test

7. Clearly state conclusion

Limit Comparison Test

Use when taking away more than one term from numerator and denominator to create Σ bn

1. Find if Σ bn converges or diverges

2. Set up Lim n→ ∞ an/bn = L

3. Solve for L and determine if it is positive and finite

   • if so, then series will do what Σ bn does

4. If L is…

   • L = 0 or pos finite # and Σ bn converges, then og series converges OR tog series will follow what Σ bn does

   • L = ∞ and Σ bn diverges, og series diverges too

Direct Comparison Test

Use if only taking one term away to make Σ bn

1. Find if Σ bn converges or diverges

2. Compare the size of Σ an and Σ bn

   • Smaller than convergent is convergent

     • an smaller than bn and bn is convergent = convergent

   • Bigger than divergent is divergent

     • an bigger than bn and bn is divergent = divergent

Solving Series Not P, Geo, Q-log, Telescoping but Positive Term Series

1. Try Divergence Test (see if lim n→ an goes to 0

   • doesn’t go to 0 = diverges, you are done

   • does go to 0 = use Integral Test

2. Try Integral Test

3. Check the following conditions to use Integral Test

   a) When plugging in # for k into denominator, can’t equal zero

   B) Derivative of f(x) must be negative

4. Compute ∫ ∞ 1 f(x)

5. Determine if integral converges or diverges

   • series will do what integral does

Solving Series w/ All or Multiple Terms to a Single n Power

Use Root Test

1. Set up Lim n → ∞ ⁿsqrt( | an | ) = L

2. Cancel terms if applicable

3. Determine value of L

   • Converges if L less than 1

   • Diverges if L greater than 1

   • Try something else if L =1

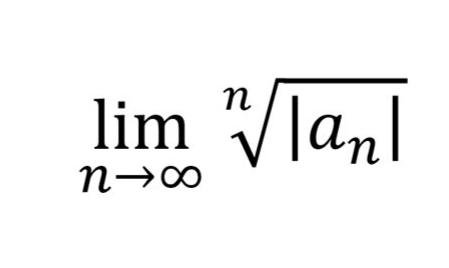
Solving Series with Factorials or Terms to Power of n

Use Ratio Test

1. Set up Lim n→ ∞ a_n+1/an = L

2. Cance terms if applicable

3. Determine value of L

   • Converges if L is less than 1

   • Diverges if L is greater than 1

   • Try something else if L = 1

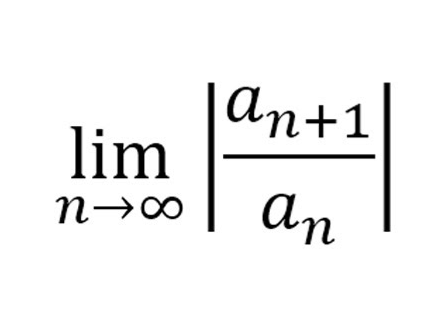
How to Write an+1

Add 1 to each n/k term

n^# → (n+1)^#

eⁿ or #ⁿ → _ⁿ⁺¹

n! → (n+1) !

ke^-k (k+1)(e^-(k+1))

nⁿ → (n+1)ⁿ⁺¹

Constant #s don’t apply and stay the same

Identify Q-Log Series

P-series with log in numerator

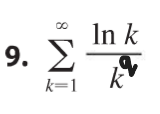
Solving Q-Log Series

1. Identify q aka the power k/n is to

2. Compare q to 1

   • Converges if q is greater than 1

   • Diverges if q is less than or equal to 1

Identify Alternating Series

When expanded, signs alternate

• (a₁, -a₂, a₃, -a₄…)

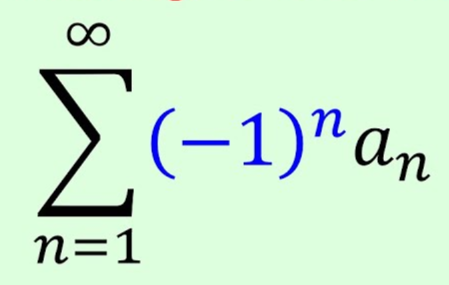
Solving Alternating Series

Use Alternating Series Test

1. Check two conditions; if both happen, converges, if not, diverges

   a) Does Lim n→ ∞ an = 0?

   b) Is a_n+1 less than an?

   • more on bottom makes term smaller

Determining Absolute Cvt, Conditional Cvt, or Divergence

1. Check for absolute convergence using Ratio Test/Root Test w/ absolute bars, Comparison Test, or Integral Test

2. For Ratio/Root tests, compare L to 1

   • Absolute convergent is L is less than 1

   • NOT absolute convergent if L is greater than 1

3. If not Absolute Cvt, check Conditional Cvt using Alternating Series Test

4. Use Alternating Series Test

   • if all conditions are met, converges, if not, diverges

Identify Alternate P-Series

They ALL converge

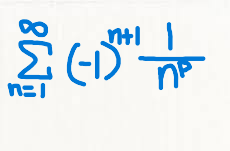
Finding Interval of Convergence

Use Ratio Test or Root Test w/ absolute bars both < 1

1. Decide which test to use

2. Plug in and cancel terms

3. Take out |x| or |x-#| or |x-#| / # and put in front of Lim

4. Solve for limit of an and multiply it by x

5. Then solve for x; what’s on the other side of < is R

6. Identify the center and draw a number line with center as middle and one point R distance to the left and another R distance to the right

7. Test each endpoint to see which gets brackets and parentheses

• 1. Let x = #

• 2. Plug in # into x in original equation

• 3. If diverges → don’t include. If converse → include

Taylor Series Centered at x = c

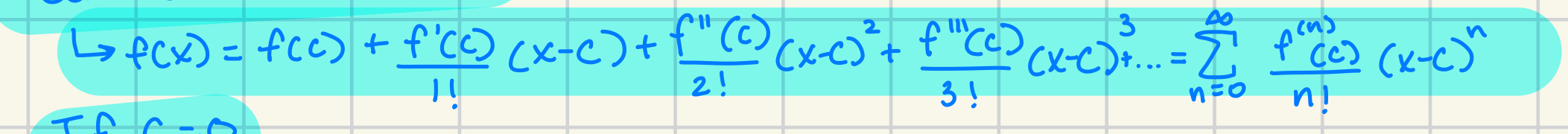
Taylor Series Centered at c = 0

Solving for Taylor Series

1. Find the first five derivatives of f(x)

2. Then, plug in value for center into x in the results for the derivatives

3. Plug into formula, simplify or cancel factorials if needed

4. Look and identify the series, check by plugging in to make sure

Maclaurin Series for e^x

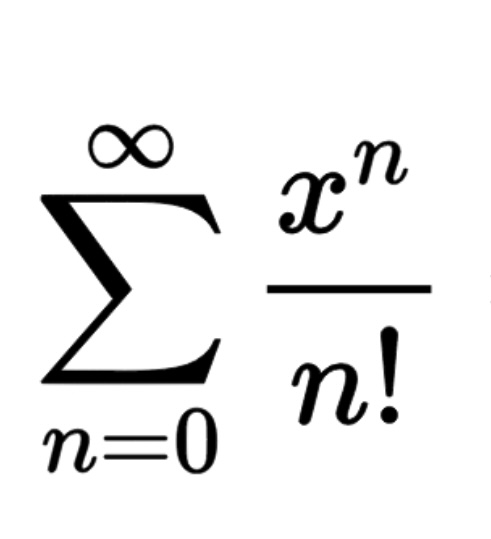
Maclaurin Series for sinx

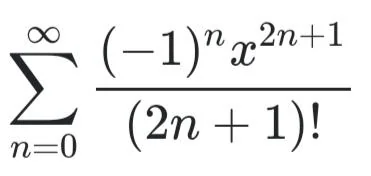
Maclaurin Series for cosx

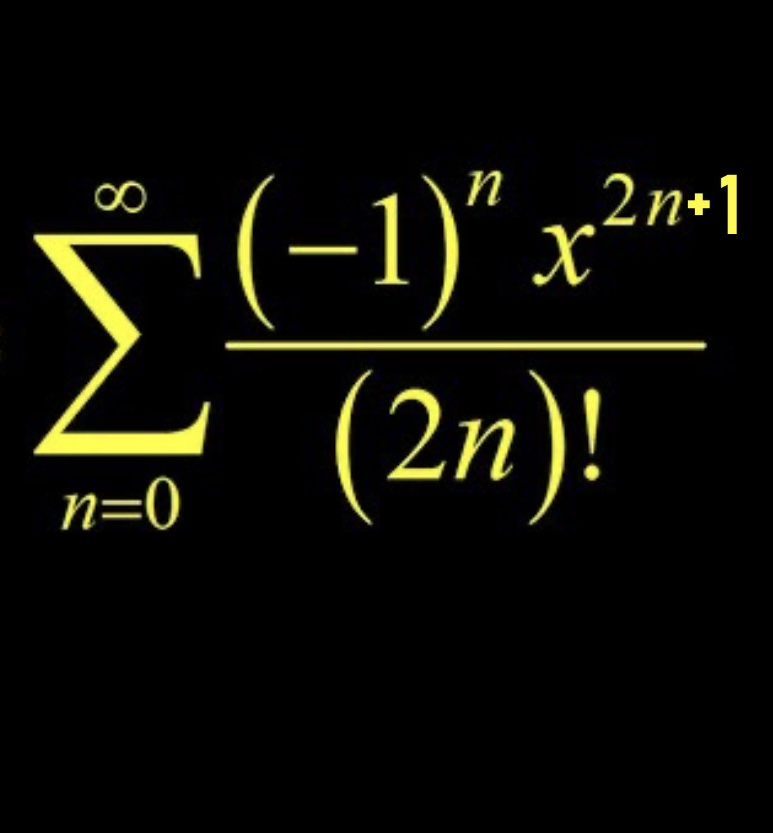
Maclaurin Series for 1 / 1 - x

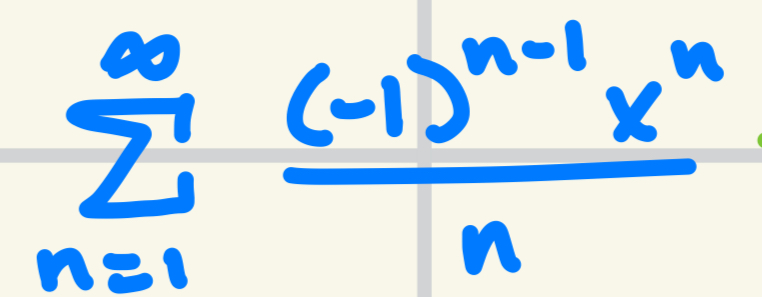
Maclaurin Series for ln(1 + x)

Maclaurin Series for arctanx

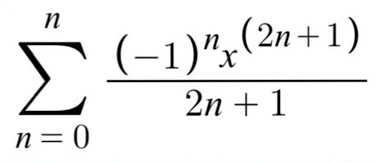
Maclaurin Series for ( 1 + x ) ^9

Finding Absolute/Conditional Cvt or Divergence for P-Series/Geo Series

Use the regular way to find convergence for them

• If converges, is absolutely convergent

• If diverges, it diverges and you’re done

Finding Absolute/Conditional Cvt or Divergence for Almost Series

Use Comparison Tests to Test for Absolute Convergence

• if converges, is absolutely convergent

• if diverges, check for conditional convergence

Finding Absolute/Conditional Cvt or Divergence using Integral Test

1. Check for absolute convergence using Integral Test

   • If converges, then absolutely converges

   • If diverges, check for conditional convergence

2. If needed, use AST to check for conditional convergence

Finding the Area Between Curves

1. Draw graph

• Note if there’s two regions because then you will also use A = A1 + A2.

1. Find points of intersection by setting equations equal to each other

2. Double check validity of points by plugging it back in to eqn made in Step 1

3. Solve for area using

4. Use points of intersection as bounds

5. Integrate

Graph of Sinx

Graph of Cosx

Graph of sqrtx

Finding Volume Doing Slicing

1. Draw the graph

• Note that x^2 + y^2 = r^2 is a circle. So if you have x^2 + y^2 = 9, then this is a circle with 3 radius

2. If needed, solve equation for y

3. Use the formula

4. Find the formula of the slice’s shape

   Square = s^2

   Equilateral triangle = (sqrt3/4)(s^2)

   Semicircle = 1/2 pi r^2, r = 1/2s

   s is top - bottom

5. Put +/- radius as integral boundaries

6. Integrate

Finding Volume with Solids in Revolution

1. Decide method of washers (disks)  or cylindrical shells and use to solve

Methods of Washers

perpendicular to axis of rev

1. Draw graph

2. Draw slice perpendicular to axis of rev

3. Find thickness (if needed, convert equns wrt to x or y depending on thickness)

4. Find R (distance between axis of rev and farthest graph)

5. Find r (distance between axis of rev and closest graph)

6. Find points of intersection by setting eqns equal to each other

• these are the integral bounds

7. Plug everything into formula

Note that R and r with just be the line of the closest or farthest equation if the axis of revolution is just x/y axis or 0

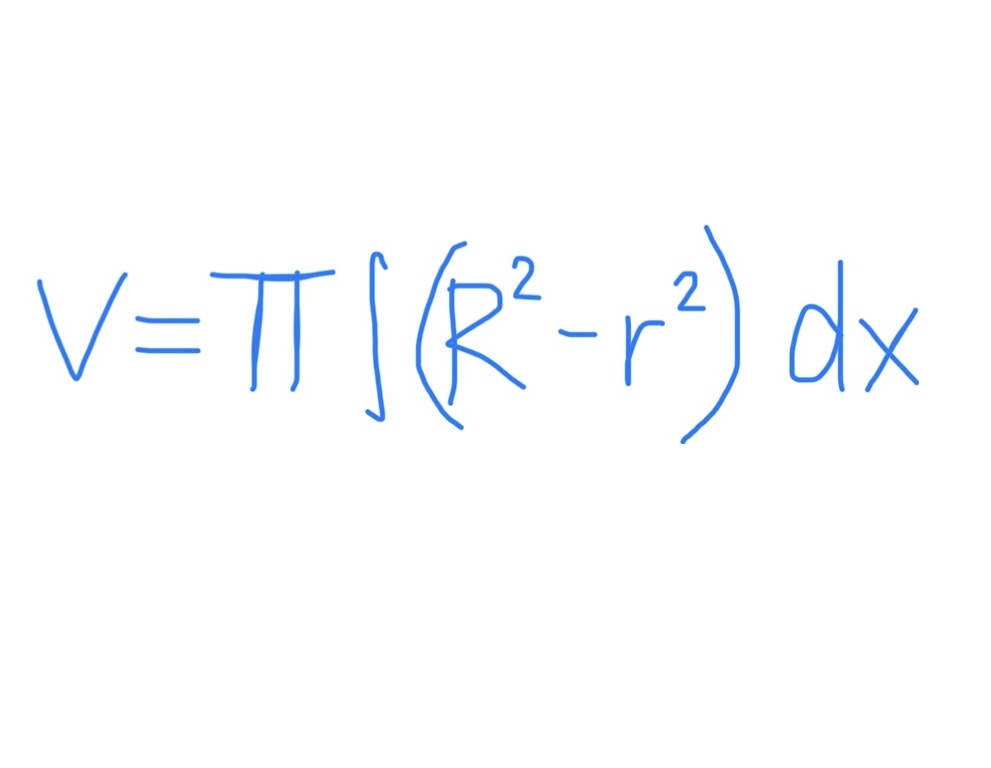
Method of Shells

parallel to axis of rev

1. Draw graph

2. Draw slice parallel to axis of rev

3. Find thickness

4. Find r (distance between axis of rev and midpoint of slice)

5. Find h (top - bottom)

6. Find points of intersection by setting eqns equal to each othe

• these are integral bounds

7. Plug into formula

Note: Midpoint of slice is normally just x

Graph of x = y^2

Graph of 2-y

Finding Work if Force Isn’t Constant

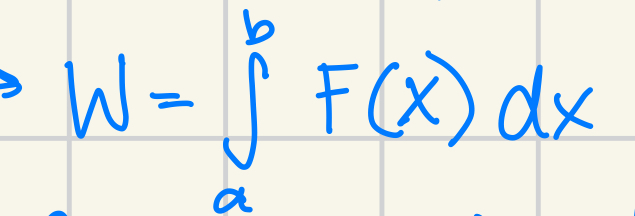
Finding Work for a Spring

1. Find k which is the spring constant using F = kx solving for k

2. Create integral

   • b: new initial length - natural length

   • a: new final length - natural length

Note: x is distance beyond natural length, k is spring constant

Finding Force of a Fluid

1. Draw picture and draw slice

2. Set up formula

3. Plug in density

4. Plug in L which is length of slice

5. Plug in depth which is height - y or depth - y

6. Plug in integral b and a

• b: depth of fluid

• a: 0

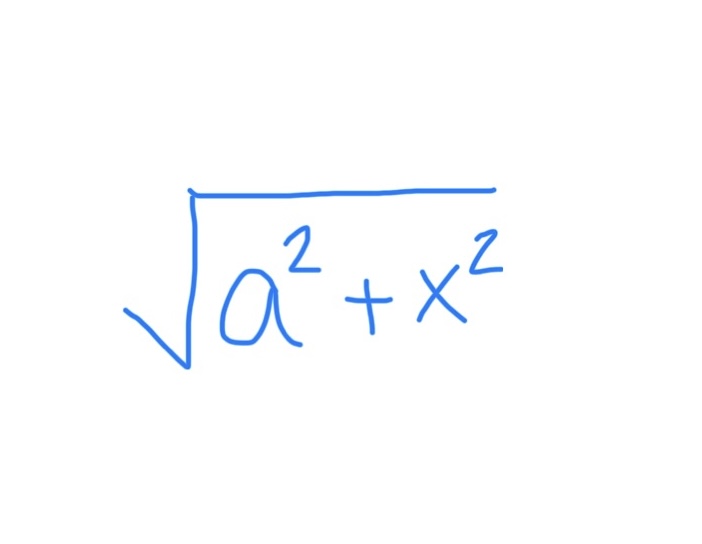
If you see this, use…

x = atanθ

dx = asec²θ dθ

1 + tan²θ = sec²θ

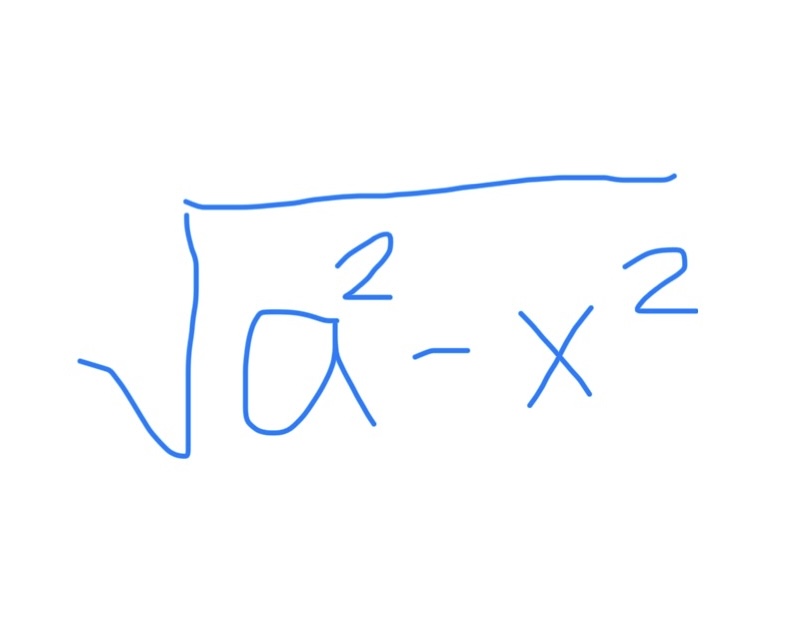
If you see this, use…

x = asinθ

dx = acosθ dθ

1 - sin²θ = cos²θ

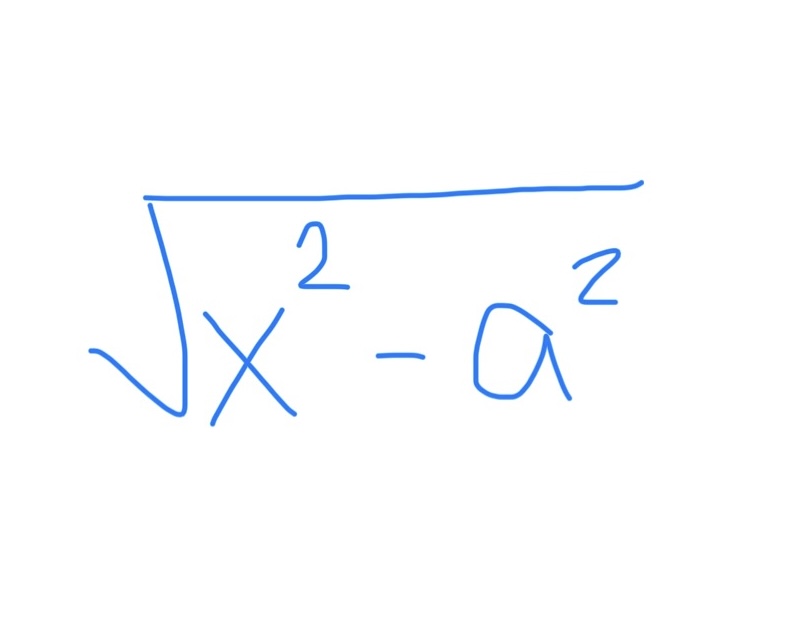
If you see this, use…

x = asecθ

dx = asecθtanθ dθ

sec²θ - 1 = tan²θ

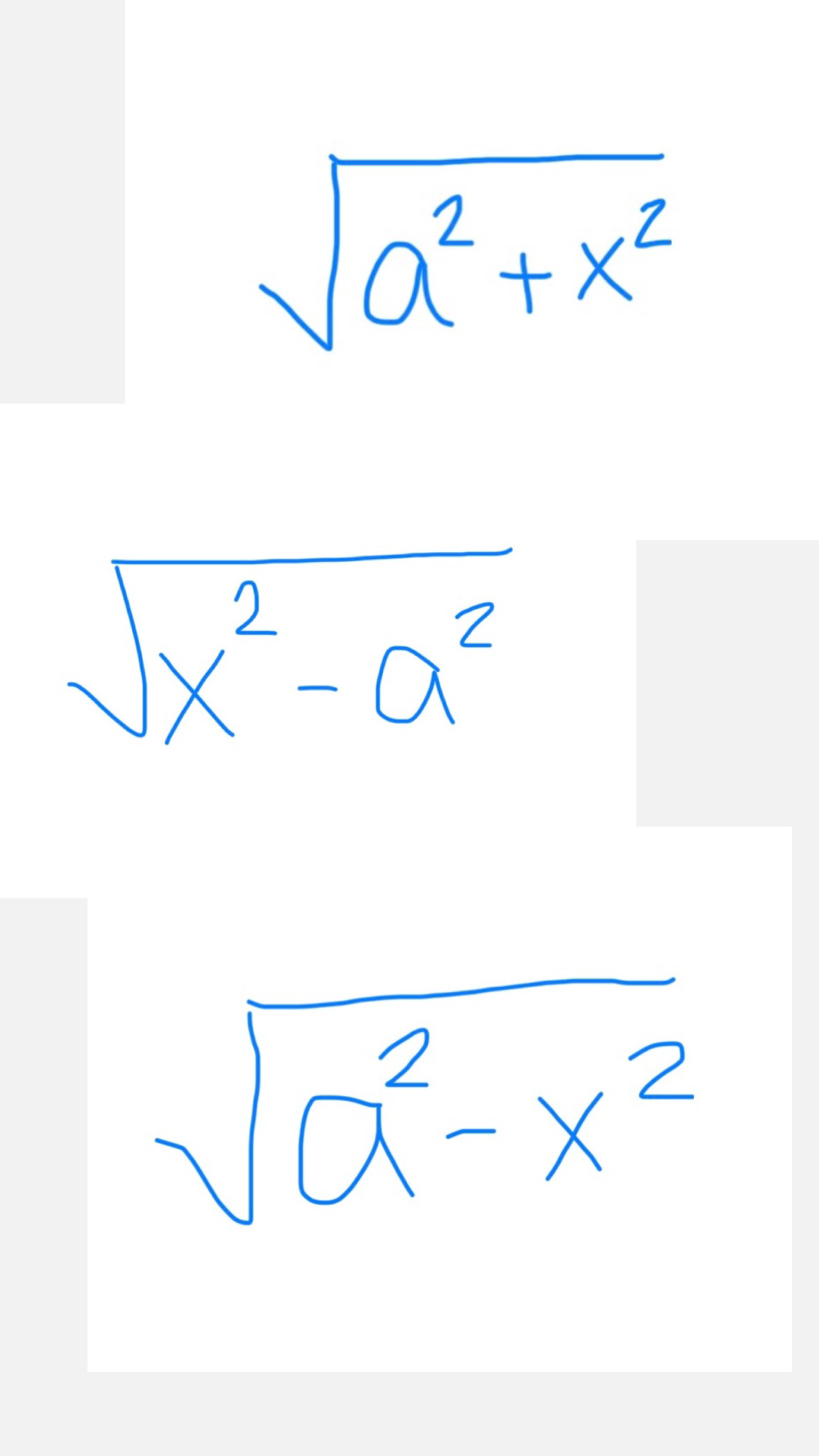
Evaluating Integral with

1. Find specific strategy and plug into x and dx

2. If possible, take out constant GCF

3. Replace with Pythagorean trig identity

4. Cancel out terms

5. Look at initial x = __ and isolate the trig function

6. Create triangle and plug in sides

• final unknown side is original sqrt in eqn

7. Replace answer with triangle values

Evaluating Integral where Num and Denom are Reduced Polynomials

• no common factors

• Deg T < Deg B

1. Factor num and denom

2. Separate eqn into 2 fractions added to each other whose denominators are each factor and numerator are variables

• Linear denom = A, B, C … numerator

• Quadratic denom = (variable)(x^one less degree) continue until get lowest degree

3. Set original equation equal to this

4. Multiply everything by original denominator to cancel out terms

5. Solve for each variable by systems of eqns

6. Plug in results for each variable into setup from Step 2

7. Integrate

∫ cos²θ

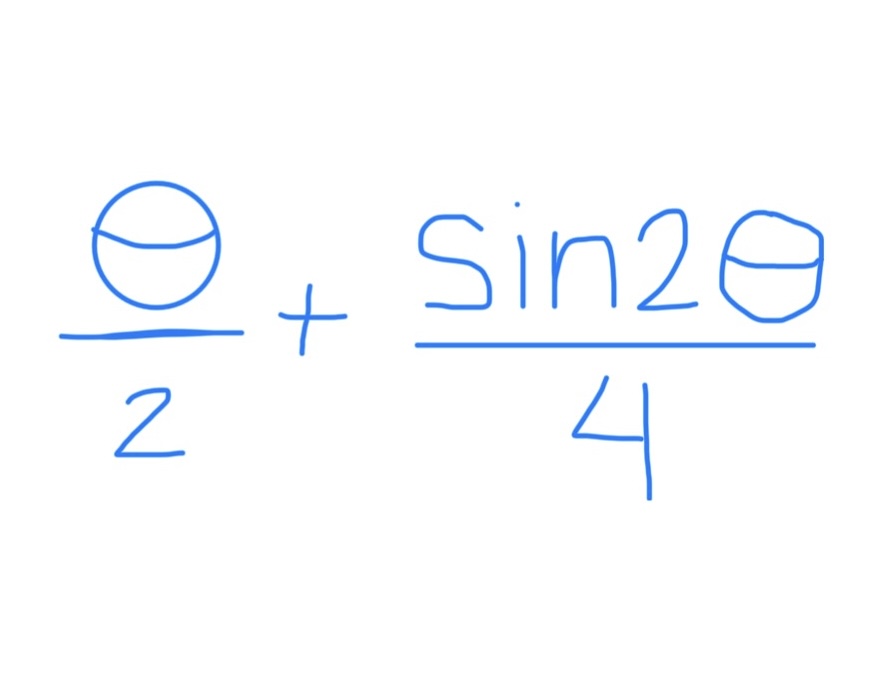
∫ sin²θ

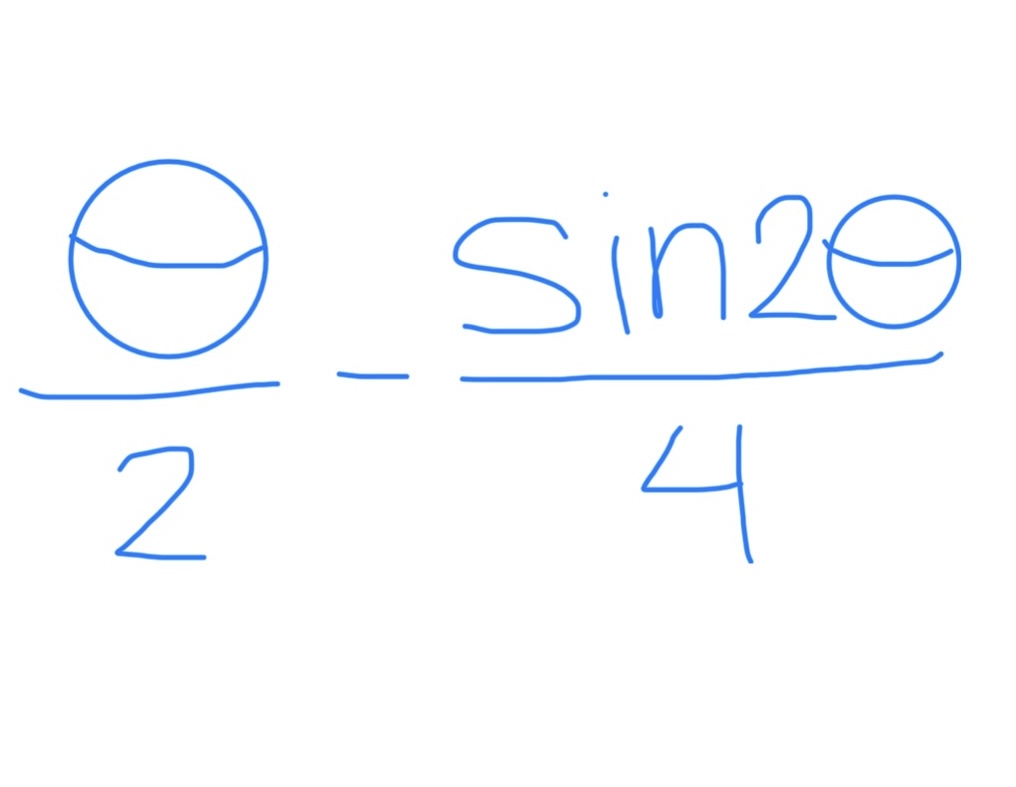
Use Table for Repeating Integration by Parts With…

xⁿsinx

xⁿcosx

xⁿe^x

Evaluating Integrals with Repeating Integration by Parts

1. Identify u and dv using LIATE

2. Create table

3. Find derivatives under u and antiderivatives under dv until you reach 0

4. Multiply diagonally and the combination of this is your answer

• the table goes +, -, +, - downward

What is Antiderivative of e^ax?

1/a e^ax

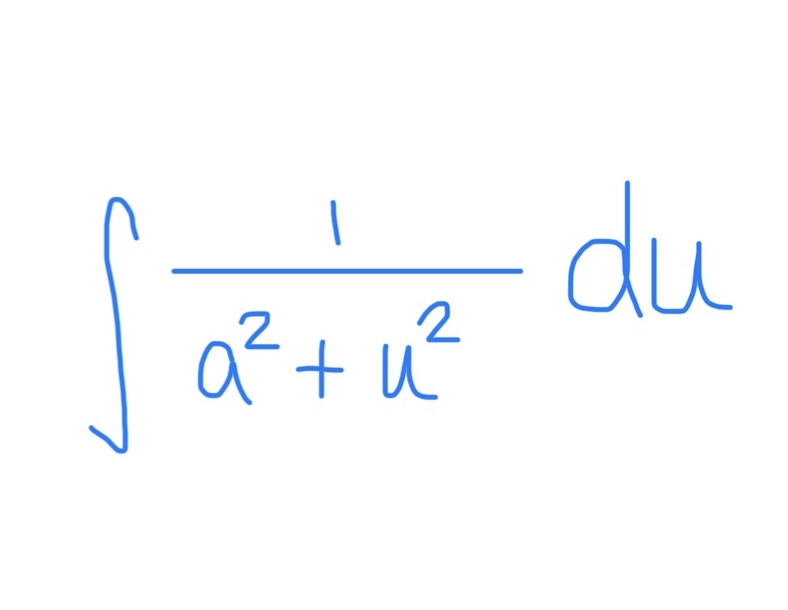
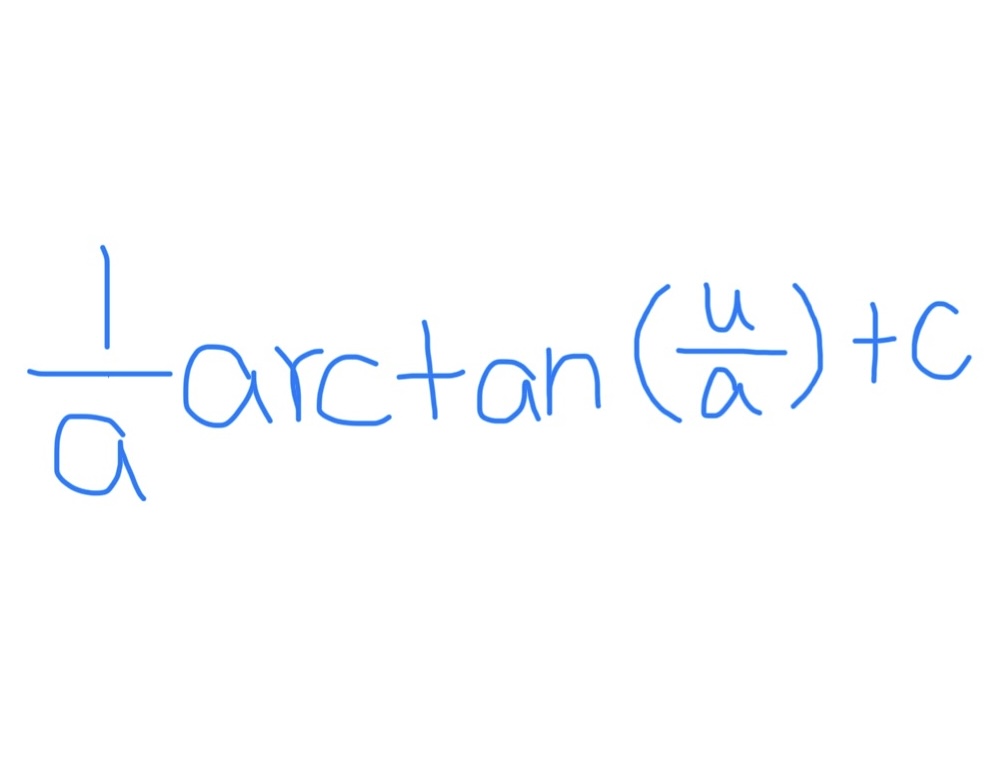
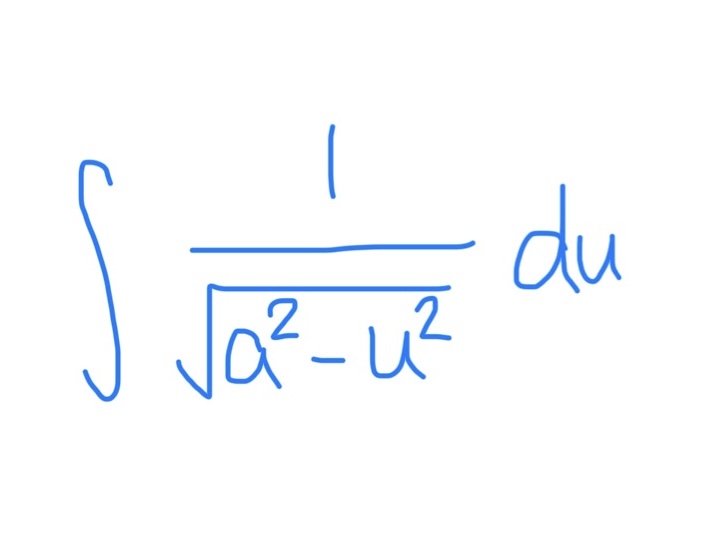
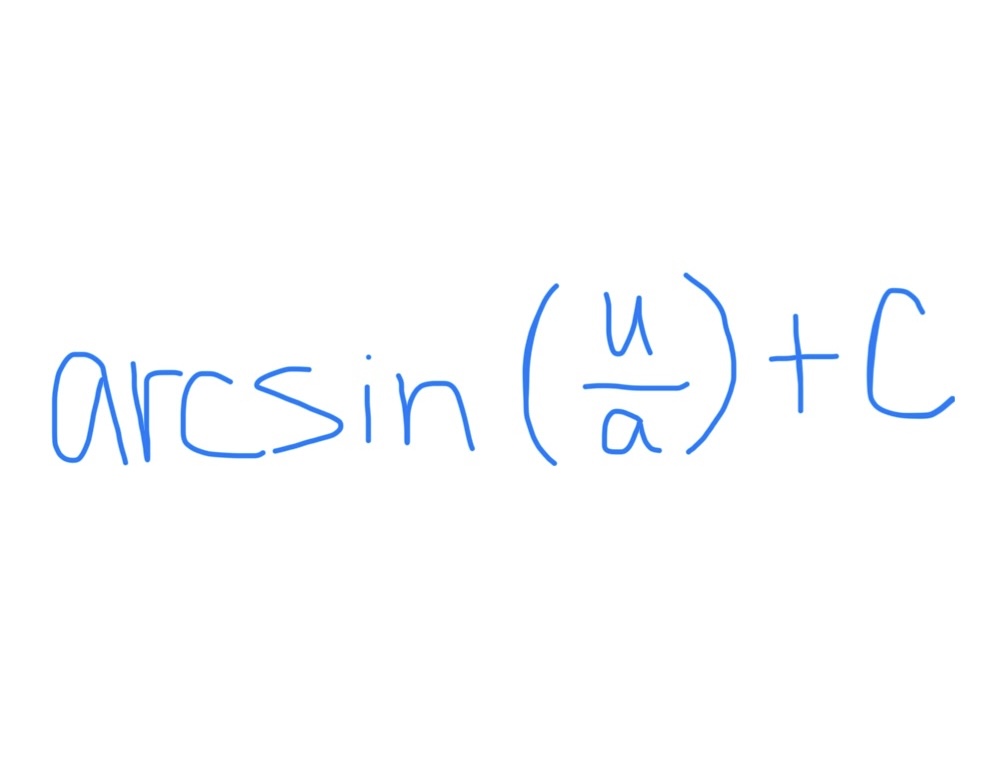
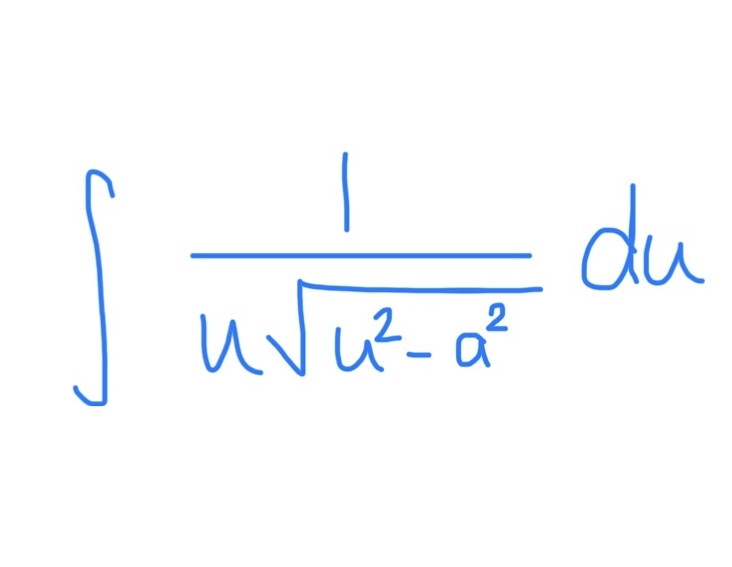
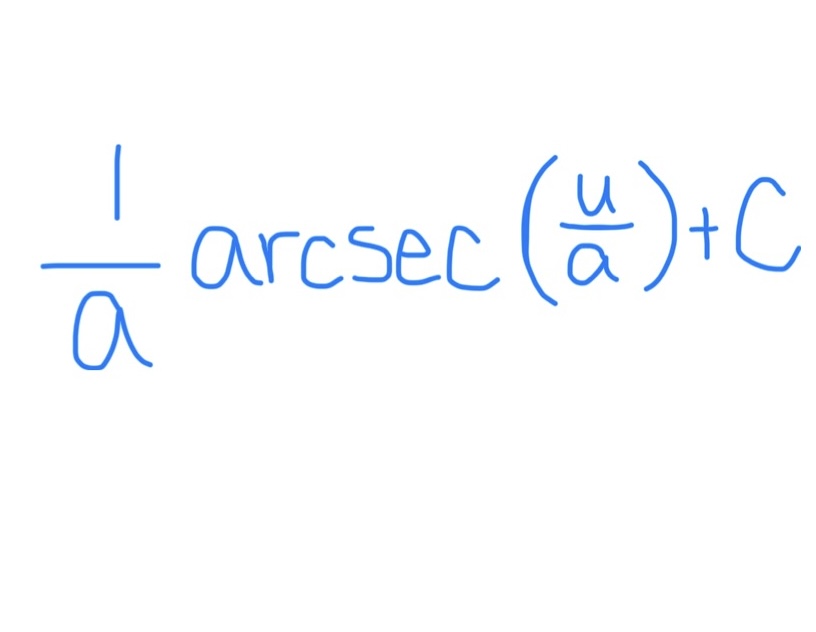
∫ tan(u) du

Ln |sec(u)| + C

∫ cot(u) du

Ln |sin(u)| + C

∫ sec(u) du

Ln |sec(u) + tan(u)| + C

∫ csc(u) du

-Ln |csc(u) + cot(u)| + C

∫ sin(u) du

-cos(u) + C

∫ cos(u) du

sin(u) + C

∫ sec²(u) du

tan(u) + C

∫ sec(u)tan(u) du

sec(u) + C

∫ csc(u)cot(u)

csc(u) + C

∫ csc²(u) du

-cot(u) + C

Derivative of arctanx

1 / 1+x²

Derivative of arcsinx

1 / sqrt(1-x²)

When To Use Integration by Parts?

… when you’re dealing with:

xⁿsinx, xⁿcosx, xⁿLnx, arctanx, arcsinx, arcsecx, xⁿe^x, e^xsinx

Evaluating Regular Integration by Parts Integrals

1. Determine u and dv using LIATE

2. Rewrite eqn as uv - ∫ v du

3. Solve solvable integrals

Identifying Circular Integration by Parts

When one step will spit out a previous function or the original function

Evaluating Circular Integration by Parts Integral

1. Determine u and dv using LIATE

2. Rewrite eqn as uv - ∫ v du

3. Solve, but when you get result that is the original eqn, take what you have so far and set the original eqn as I and then set everything equal to I

4. Solve for I to get answer

How to Integrate ∫ sinⁿ(x) cosⁿ(x) dx Where There’s an Odd Power on Sin(x) or Cos(x)

1. Pull out a factor from whichever trig has odd power and put it with dx

2. Replace odd trig using sin²(x) + cos²(x) = 1

3. Trig function that wasn’t odd is u

   • cos(x) = odd —> u = sin(x), du = cos(x)

How to Integrate ∫ sinⁿ(x) cos^m(x) dx Where Both Powers are Even

Use power reduction formulas

• sin²(x) = (1-cos(2x)) / 2

• cos²(x) = (1+cos(2x)) / 2

1. Deconstruct all trig into (__)²

2. Replace w/ power reduction formulas

3. Integrate

How to Integrate ∫ tanⁿ(x) sec^m(x) When Power of Sec(x) is Even

1. Pull out a factor from sec(x) so that it becomes sec²(x) and put it with dx

2. Replace rest of sec(x) with sec²(x) = tan²(x) + 1

   • except the sec(x) that’s part of dx

3. Do u-substitution where

   • u = tan(x)

   • du = sec²(x) dx

How to Integrate ∫ tanⁿ(x) sec^m(x) When Power of Tan(x) is Odd

1. Pull out a factor from tan(x) so that it becomes tan²(x) and put it with dx. Also pull out a factor from sec(x) and put it with dx

2. Replace rest of tan(x) with tan²(x) = sec²(x) -1

3. Do u-substitution where…

   • u = sec(x)

   • du = sec(x)tan(x) dx

How to Integrate Individual Trig Functions with Even Powers

1. Use power reduction rule

   • sin²(x) = (1-cos(2x)) / 2

   • cos²(x) = (1+cos(2x)) / 2

2. Then use u-du integal

How to Integrate Individual Trig Functions with OddPowers

Use u-du integral

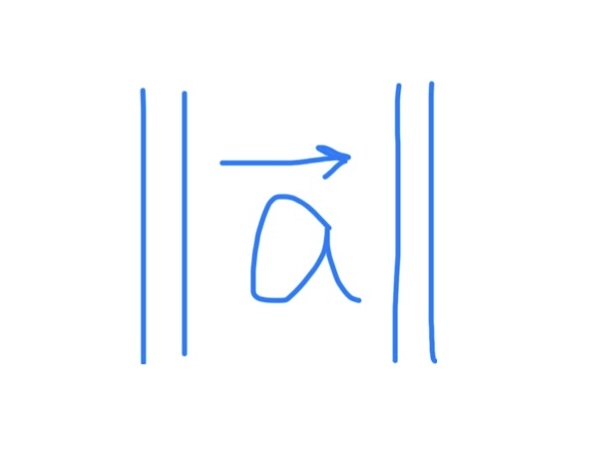
Unit Vector Formula

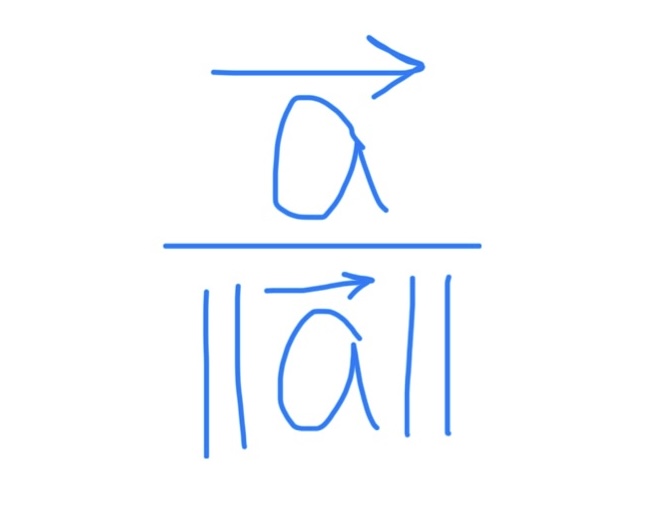
Magnitude Formula

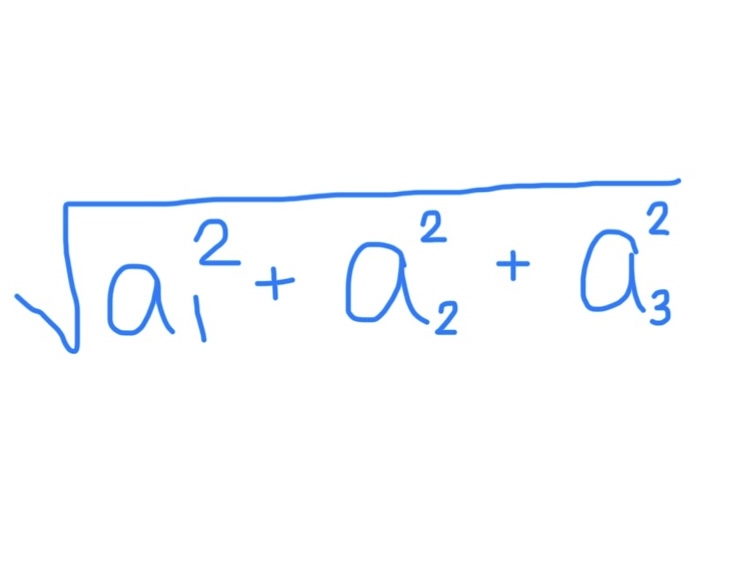
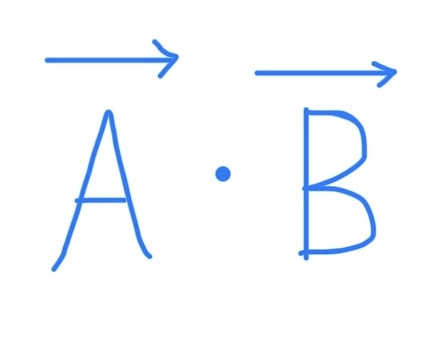
Dot Product Formula

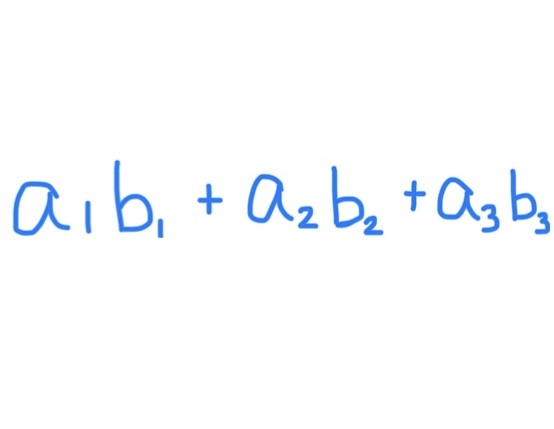
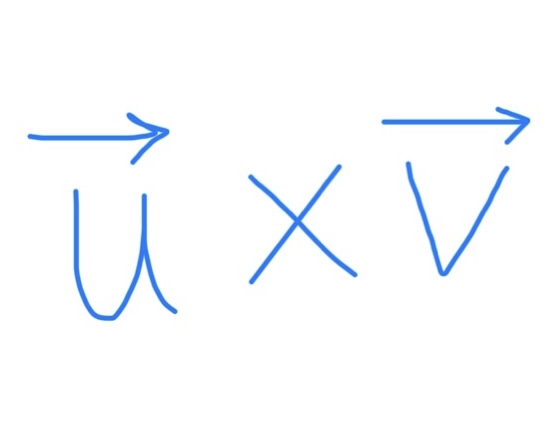
How to Solve Cross Product

1. Set up i, j, k table with the vector coordinates put in horizontally

2. You’re aiming for the form |__| i - |__| j + |__| k

• Cover the letter you’re trying to find |__| for and put the numbers you can see in same order

3. Cross multiply and subtract (main diagonal - reverse diagonal)

4. Then take out the i, j, k and your answer is the numbers in <___>

To Find Angle Between 2 Vectors

Use cosθ formula and solve for θ by making cosθ go in other side as cos^-1

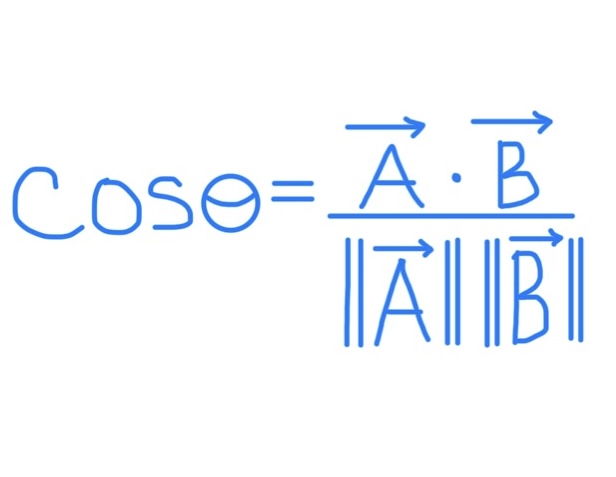
A Vector is Perpendicular If …

If dot product of both vectors = 0

A Vector is Parallel If …

If you can get vector A to vector B by multiplying by a scalar/fixed #

Power Reduction Formula for Sin²x

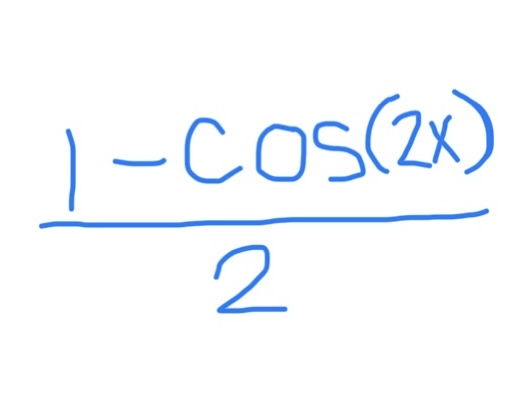
Power Reduction Formula for Cos²x

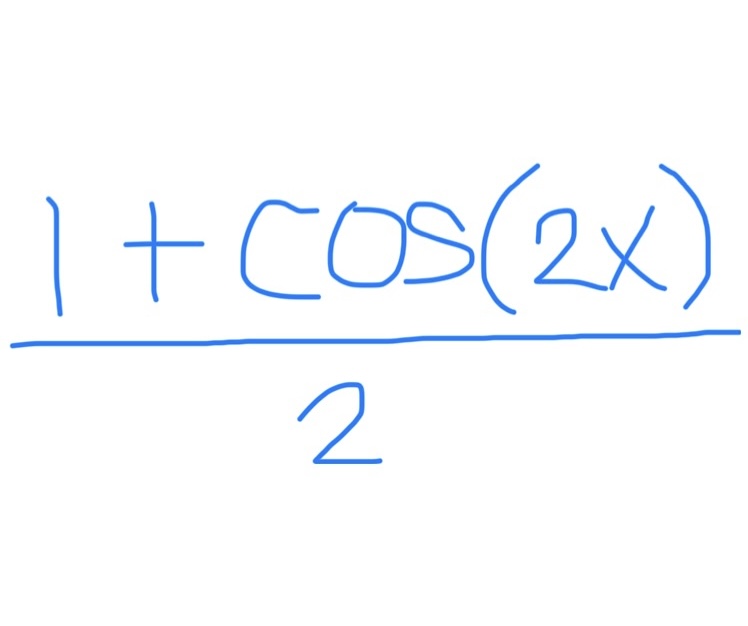
Arc Length Formula