4 Meccanica Razionale, capitolo 4 Lavoro e potenziale

da che cosa dipende in modo generale la forza

F = F( P, v, t)

quali sono i due tipi di lavoro infinitesimi che esistono

1. lavoro infinitesimo possibile
   ∂L = F × ∂P = Fx∂x + Fy∂y + Fz∂z
   prodotto scalare della forza e di uno spostamento possibile
   (spostamento possibile, tiene conto dei vincoli e della loro eventuale dipendenza dal tempo)

2. lavoro infinitesimo virtuale
   δL = F × δP = Fxδx + Fyδy + Fzδz
   prodotto scalare della forza per uno spostamento virtuale
   (spostamento virutale, tiene conto dei vincoli ma non della loro dipendenza dal tempo, si puo pensare con uno spostamento a velocità infinita)

come si calcola il lavoro lungo una curva

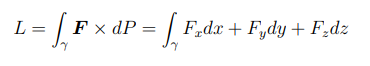
quale è il rapporto tra lavoro e potenza

calcolando la potenza lungo un periodo di tempo;
dove W = F x v

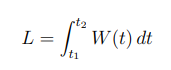
definizione di forza conservativa

una forza è conservativa se la forma differenziale del suo lavoro è un differenziale esatto
cioè se esiste una funzione regolare U tale che

dL = dU

come è definito il potenziale di una forza, che caratteristiche ha la funzioen potenziale

il potenziale è una funzione ad un solo valore, regolare tale che per F forza conservativa vale
dL = dU

oppure in termini vettoriali:
F = ∇U

il potenziale è definito a meno di una costante additiva arbitraria

quali sono le piu importanti caratteristiche del lavoro di una forza conservativa

1. il lavoro di una forza conservativa lungo un percorso qualsiasi equivale alla differenza di potenziale tra il punto finale e iniziale:
   U(P2) - U(P1)

2. il lavoro per un percorso chiuso è nullo essendo P1 = P2
   L = 0

quando una forza è conservativa

• F conservativa → rotore di f nullo, ma non il contrario

• se il dominio dove è definita F è semplicemente connesso allora vale:
  F conservativa ←→rotore nullo

scrivere la forma differenziale che descrive il lavoro generato da un sistema di Forze applicate ad un corpo rigido
ricavare la formula

δL = R × δΩ + MΩ × δψ
dove R è la risultante delle forze applicate, MΩ il momento rispetto ad un punto Ω.
Con δψ = ω*dt

come si calcola il lavoro di una coppia

δL = MΩ × δψ
Con δψ = ω*dt

il lavoro di un sistema di forze applicate ad un corpo cambia con trasformazioni elementari sul sistema di forze applicate

dato che il lavoro dipende solamente dalla risultante R e dal momento risultante M che sono invarianti per trasformazioni elementari anche il lavoro lo è se si parla di un corpo rigido

come si calcola il lavoro di un sistema di forze applicate ad un sistema olonomo,
DERIVARE formula

causa del sistema olonomo, si distingue fra spostamenti possibili e spostamenti virtuali,
nella formula Q sta per la forza generalizzata di Lagrange
W è la potenza sviluppata dalle forze al variare del vincolo

definizione di un sistema di forze conservative, quali proprietà ha U

Un sistema di forze si dice conservativo quando la forma differenziale del lavoro totale delle forze è un differenziale esatto, cioè è il differenziale di una funzione regolare a un sol valore U

• dL = dU

scrivere la relazione fondamentale che collega il lavoro infinitesimo virtuale di un sistema olonomo con la forza generalizzata

scrivere il lavoro di un sistema di forze applicate ad un sistema olonomo in:

1. forma differenziale con spostamenti virtuali

2. forma differenziale con spostamenti possibili

• Spostamenti possiblie: ∂L = Q × ∂q + W ∂t

• Spostamenti virtuale: δL = Q × δq

che cosa dice il teorema della energia cinetica

Dice che la variazione della energia cinetica di un sistema con forze attive è pari alla variazione del lavoro del sistema:

dL = dT

come si possono calcolare le forze generalizzate di Lagrange, quale caratteristica deve avere il sistema di forze applicate?

come si calcola il potenziale della forza gravitazionale, a che cosa bisogna fare attenzione

U = mg x OP + C

bisogna fare attenzione al verso del sistema di riferimento, dato che se la asse è concorde con il vettore g allora
U = mgy + C

se invece è discorde
U = -m*g*y + C

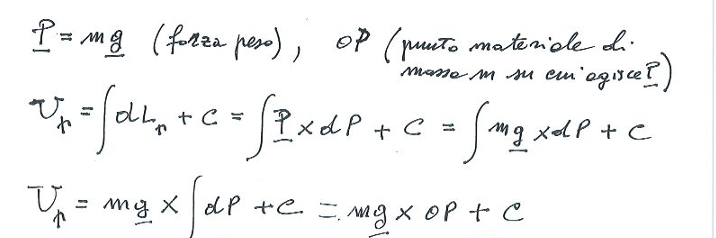
quale è la forma differenziale per il lavoro di un sistema di forze applicate ad un corpo rigido? RICAVARE!

come si calcola il lavoro di una coppia

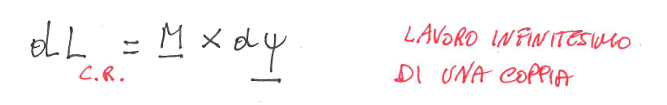
come si calcola il potenziale di una molla
a che cosa bisogna fare attenzione

il potenziale di una molla è sempre negativo