3.1 Decision Problems & Undecidable Problems

What does For every alphabet Σ, fix distinct strings w₁, w₂ ∈ Σ* mean

For any alphabet Σ, we choose two different strings w₁ and w₂ made up of symbols from Σ, and we’ll use those same two strings in whatever definition or proof follows.

For every alphabet Σ, fix distinct strings w1, w2 ∈ Σ*.

The characteristic function of a language L ⊆ Σ* is what?

The function χL : Σ* → Σ*

What is the function χL : Σ* → Σ* defined by?

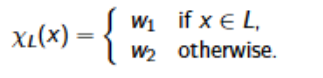
Prove a language L is decidable if its characteristic χL is computable

Let M be a TM computing χL. Extend M to a machine M’ such that after M has halted, M’ checks whether M has written w₁ or w₂ and either accepts (case w₁) or rejects (case w₂).

Prove a language L is decidable only if its characteristic χL is computable

Let M be a halting TM that accepts L. Extends M to a machine M’ such that after M accepts (rejects) its input, M’ clears the tape, writes w₁ (w₂), rewinds the tape head and accepts.

What is the set of a partial function f: Σ* → Σ*

Graph(f) = {(v, w) ∈ Σ* x Σ* | f(v) = w},

How can Graph(f) = {(v, w) ∈ Σ* x Σ* | f(v) = w} be turned into a language over Σ ∪ {#}:

When is a partial function f: Σ* → Σ* computable?

If and only if Graph#(f) is semidecidable

When is a total function f: Σ* → Σ* computable?

if and only if Graph#(f) is decidable

What is a decision problem?

A set of questions each of which has the answer yes or no

The questions are the instances of the decision problem, depending on their answers they are yes-instances or no-instances

Input: A finite automaton M and w ∈ Σ*
Question: Is Is w ∈ L(M)?

Problem domain: D = {(M, w ) | M is a FA and w ∈ Σ*}

What is the yes instance and the no instance?

Yes-instances: {(M, w ) ∈ D | w ∈ L(M)}

No-instances: {(M, w ) ∈ D | w !∈ L(M)}

How do you solve a decision problem P by TMs?

instances I are encoded as strings enc(I) over some alphabet Σ.

1. Y(P) is the language of encoded yes-instances

2. N(P) is the language of encoded no-instances.

3. E(P) = Y(P) ∪ N(P) consists of all encoded instances.

When is an encoding enc reasonable?

Assumption: We will only deal with encodings that are reasonable

→ Y(P) ∩ N(P) = ∅
→ E(P) is decidable
→ There is a decoding algorithm which given a code w ∈ E(P) ,constructs an instance I such that enc(I ) = w

When is a decision problem decidable (solvable)?

If Y(P) is decidable, otherwise P is undecidable (or unsolvable)

When is a decision problem P semidecidable?

If Y(P) is semidecidable.

What is the complement of a decision problem P?

Swapped yes or no answers

Prove if a decision problem P is decidable, then its complement is also decidable

Solve the self accepting problem (SAP):

Input: Turing Machine TM

Question: Does M accept e(M) (Is e(M) ∈ L(M)?)

Problem {M | M is a TM}

Using our encoding e for Turing machines, we have

Y(SAP) = {e(M) | M is a TM and e(M) ∈ L(M)} = SA.

Hence the theorem follows from the fact that SA is undecidable but semidecidable.

Input: TM M and a string w

Question: Does M accept w ? (Is w ∈ L(M)?)

We reduce SAP to this problem, that is, we show that thedecidability of MP implies the decidability of SAP. Since SAP is undecidable, MP must be undecidable, too. Suppose that MP is decidable. Then the language Y(MP) of encoded yes-instances is decidable, that is, there is a TM TMP which accepts Y(MP) and halts on all inputs.

Prove the halting problem is undecidable but semidecidable

Input: A Turing Machine M and a string w ∈ Σ*

Question: Does M reach a halting configuraiton on input w?

A simple reduction of MP to HP shows that HP is undecidable(left as an exercise).To show that HP is semidecidable, modify a universal Turing machine U to a machine U′ which accepts an input e(M)e(w ) if and only if U halts on e(M)e(w ). Then Y(HP) = L(U′), hence HP is semidecidable.