Physics - Impulse and Momentum

What is the momentum of a 100 kg motorbike travelling at 10m/s?

p = mv

p = 100 kg * 10 m/s

p = +1.0 × 10³ kg * m/s

A compact car, mass 725 kg, is moving at +100km/h.

a) Find its momentum

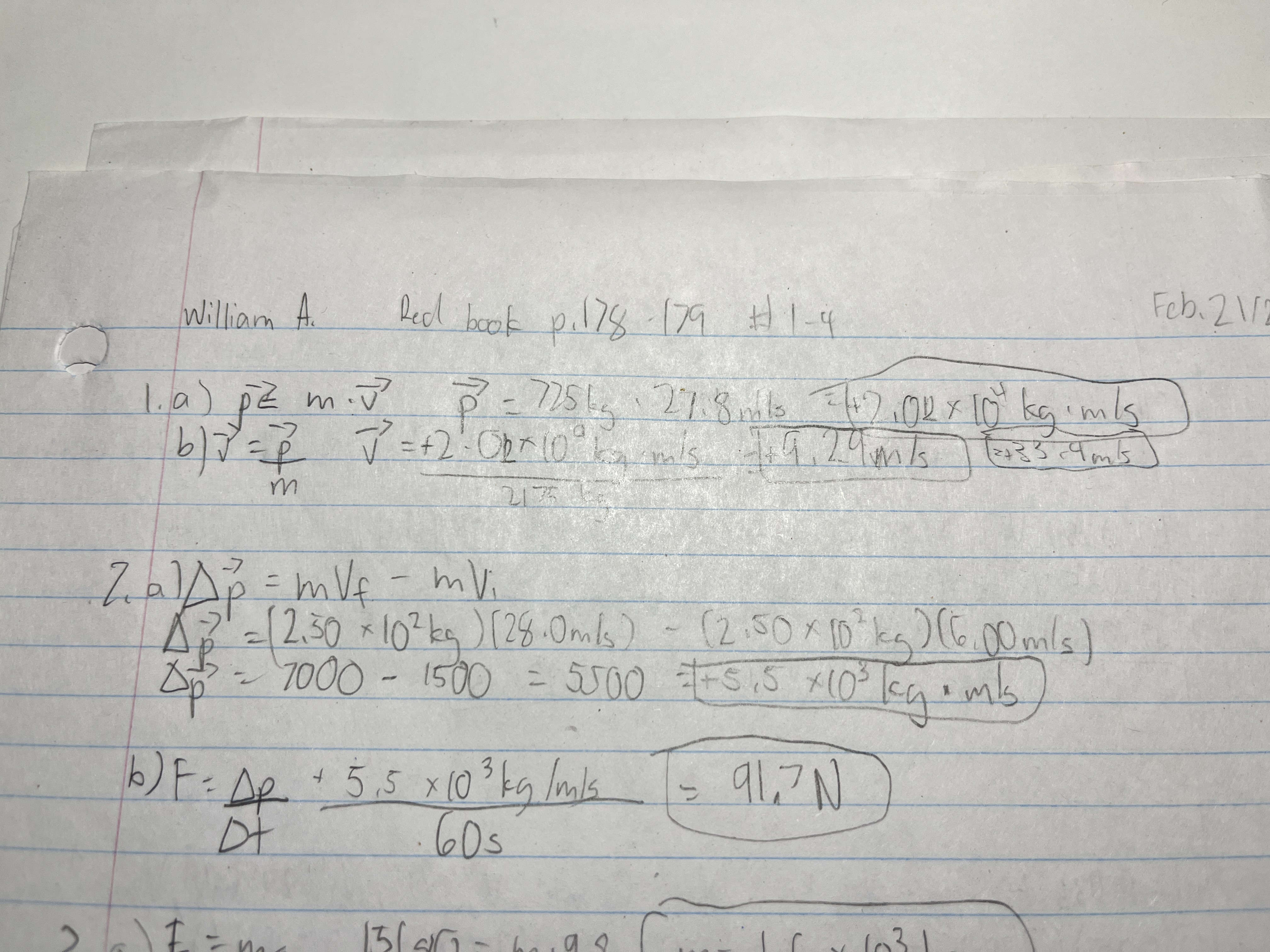
A compact car, mass 725 kg, is moving at +100km/h.

b) At what velocity is the momentum of a larger car, mass 2175 kg, equal to that of the smaller car?

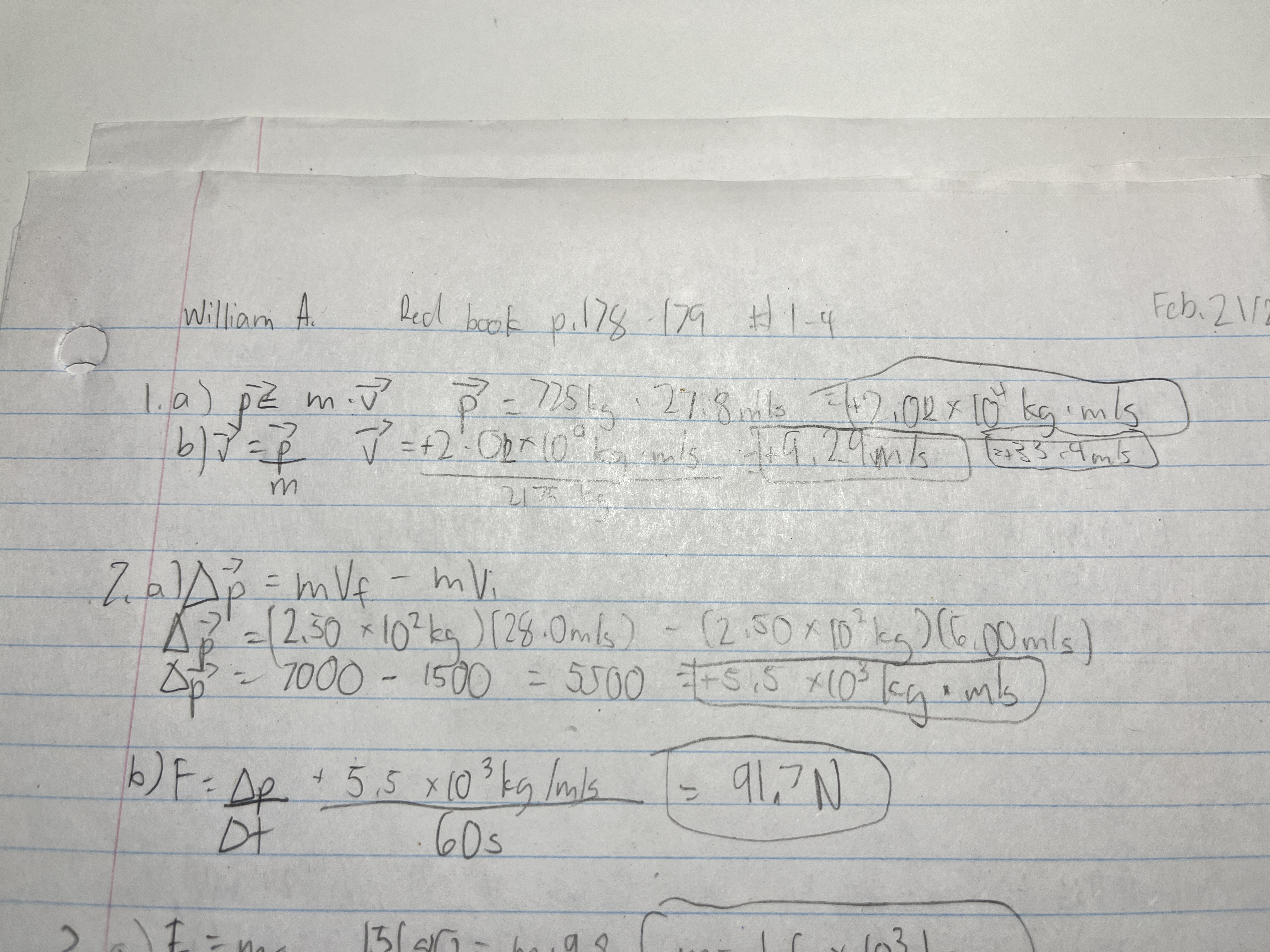
A snowmobile has a mass of 2.50 × 10² kg. A constant force is exerted on it for 60.0 s. The snowmobile’s initial velocity is 6.00 m/s and its final velocity 28.0 m/s.

a) What is its change in momentum?

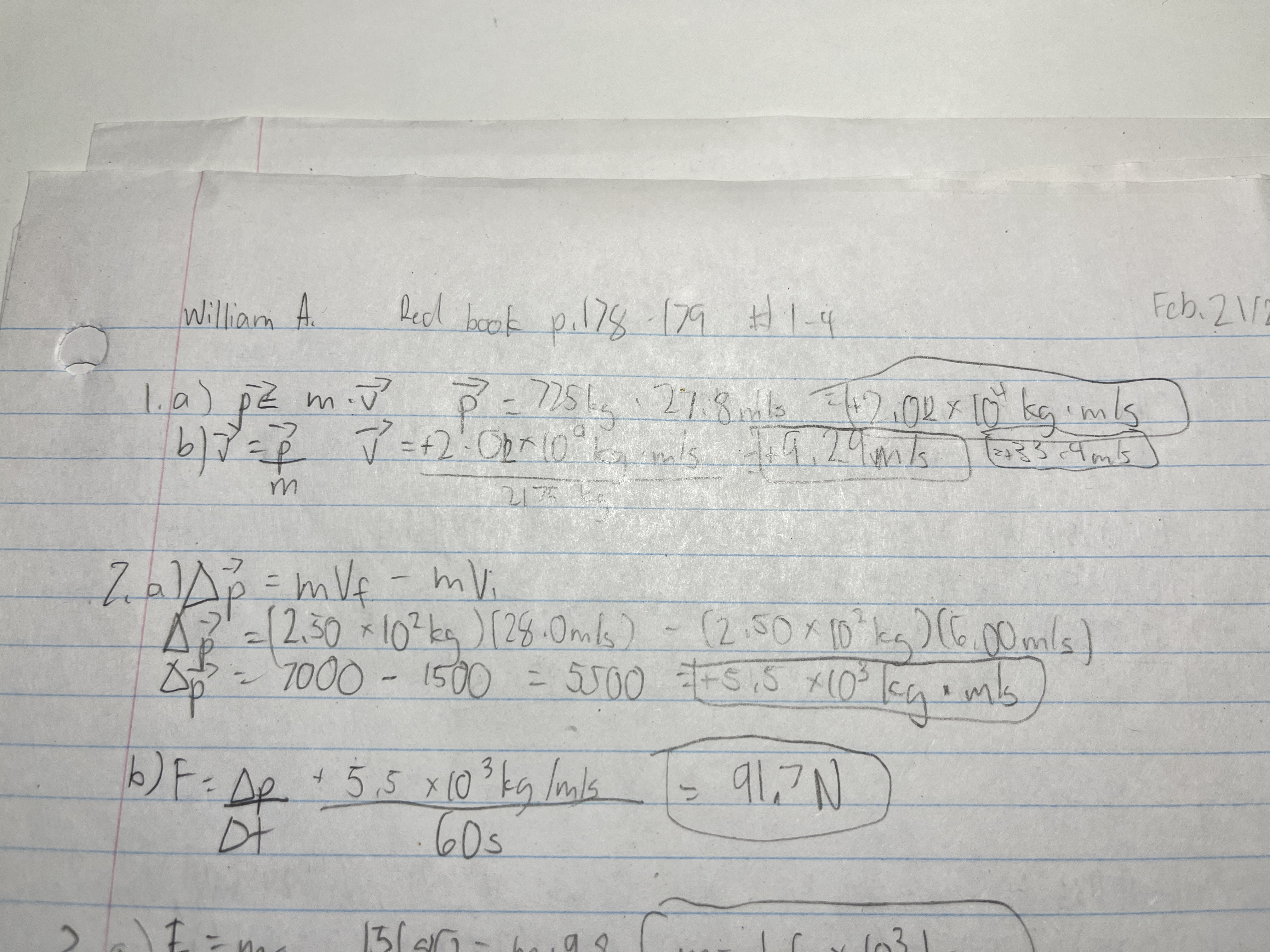
A snowmobile has a mass of 2.50 × 10² kg. A constant force is exerted on it for 60.0 s. The snowmobile’s initial velocity is 6.00 m/s and its final velocity 28.0 m/s.

b) What is the magnitude of the force exerted on it?

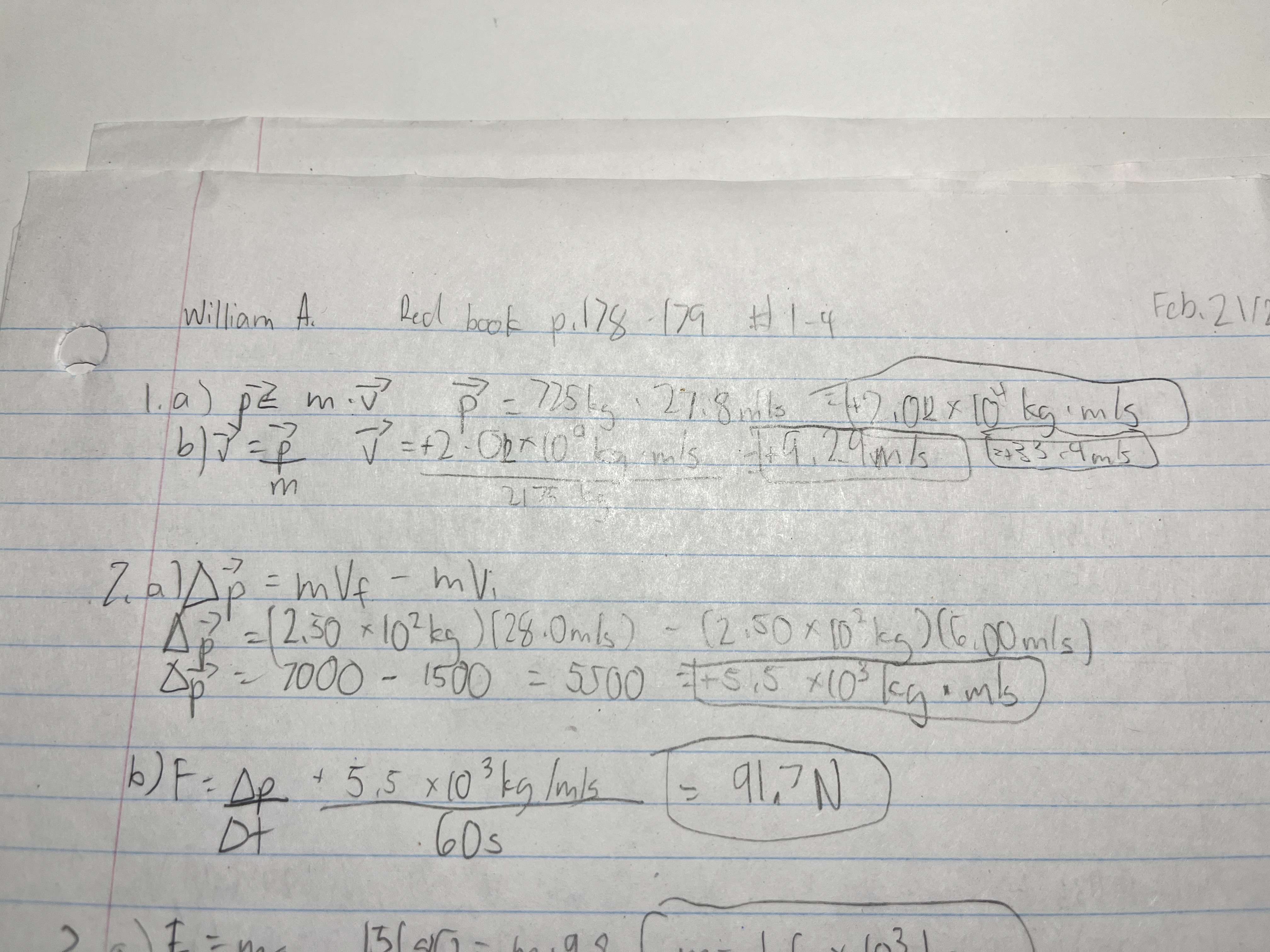
The brakes exert a 6.40 × 10² N force on a car weighing 15680 N and moving at 20.0 m/s. The car finally stops.

a) What is the car’s mass?

The brakes exert a 6.40 × 10² N force on a car weighing 15680 N and moving at 20.0 m/s. The car finally stops.

b) What is its initial momentum?

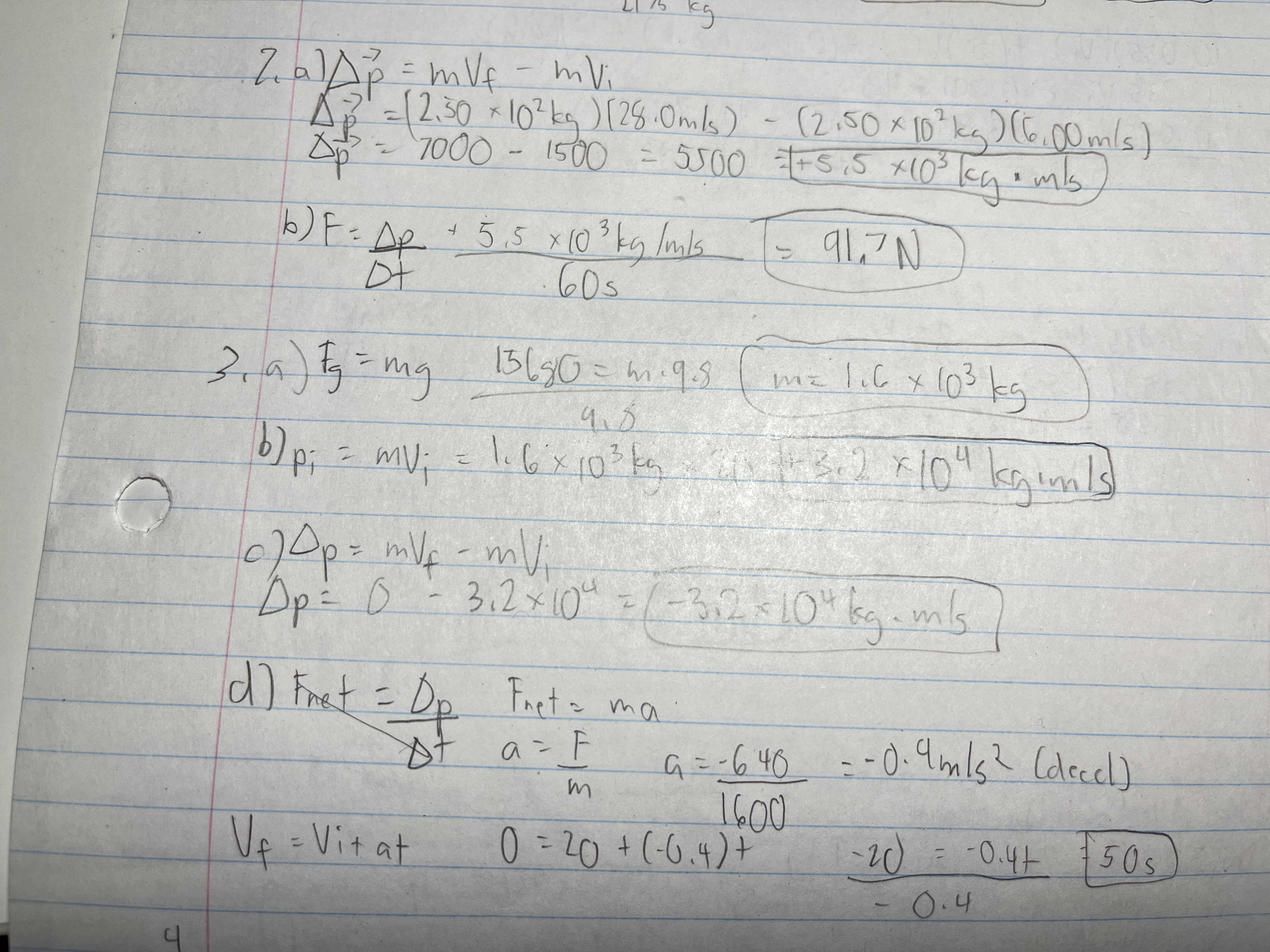
The brakes exert a 6.40 × 10² N force on a car weighing 15680 N and moving at 20.0 m/s. The car finally stops.

c) What is the change in the car’s momentum?

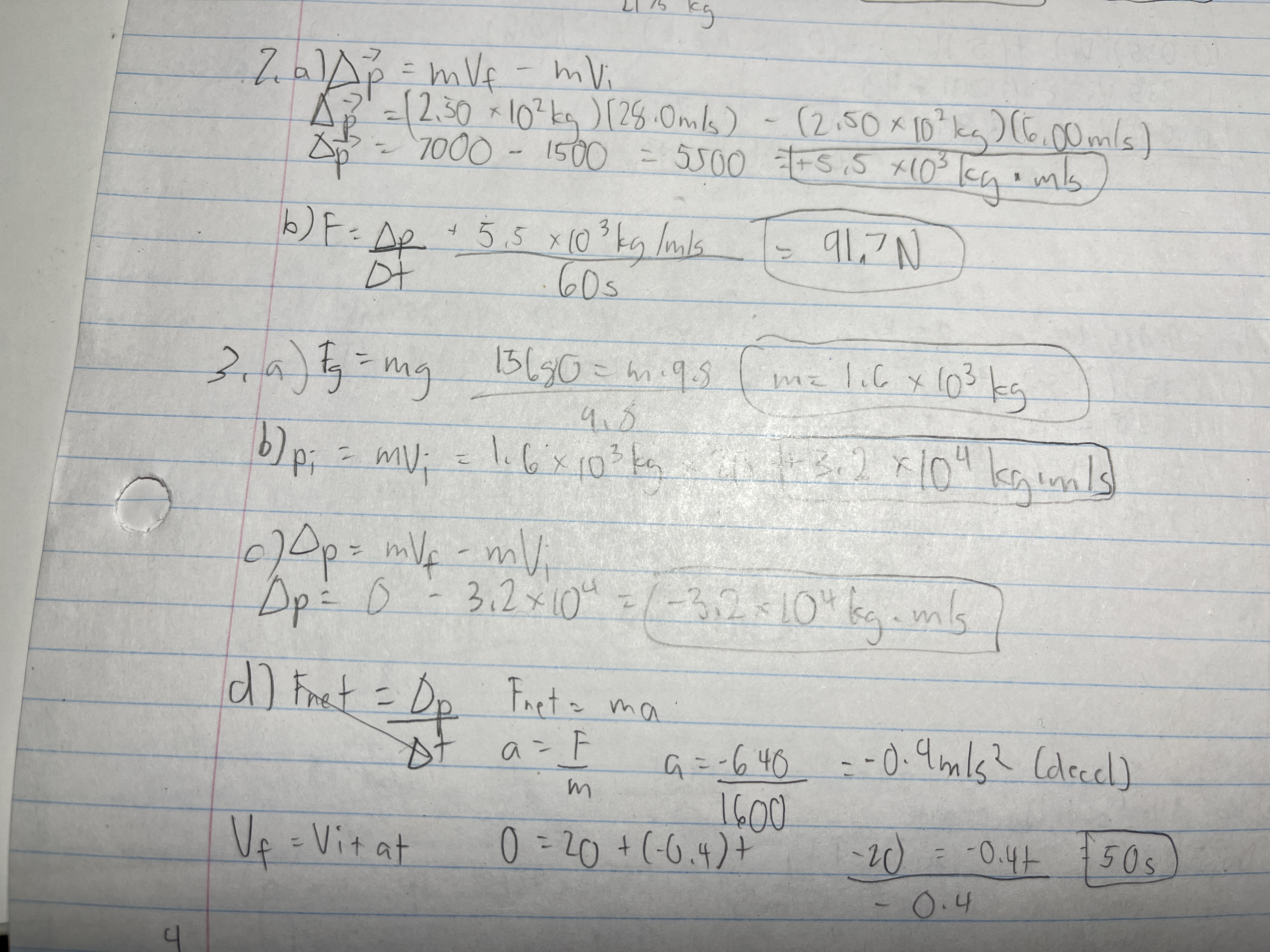
The brakes exert a 6.40 × 10² N force on a car weighing 15680 N and moving at 20.0 m/s. The car finally stops.

d) How long does the braking force act on the car to bring it to a halt?

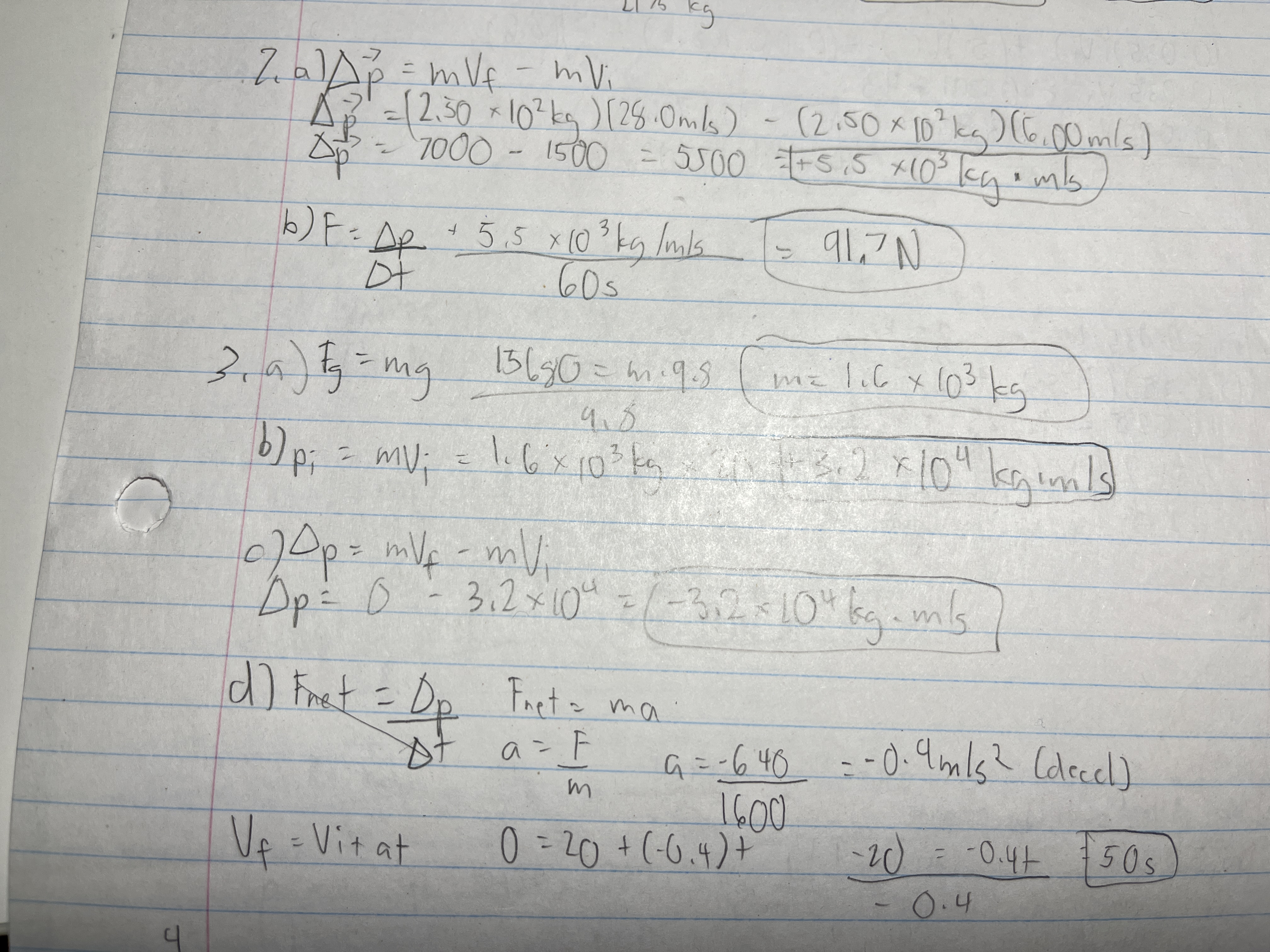
A 0.105 kg hockey puck moving at 48 m/s is caught by a 75 kg goalie at rest. With what speed does the goalie slide the ice?

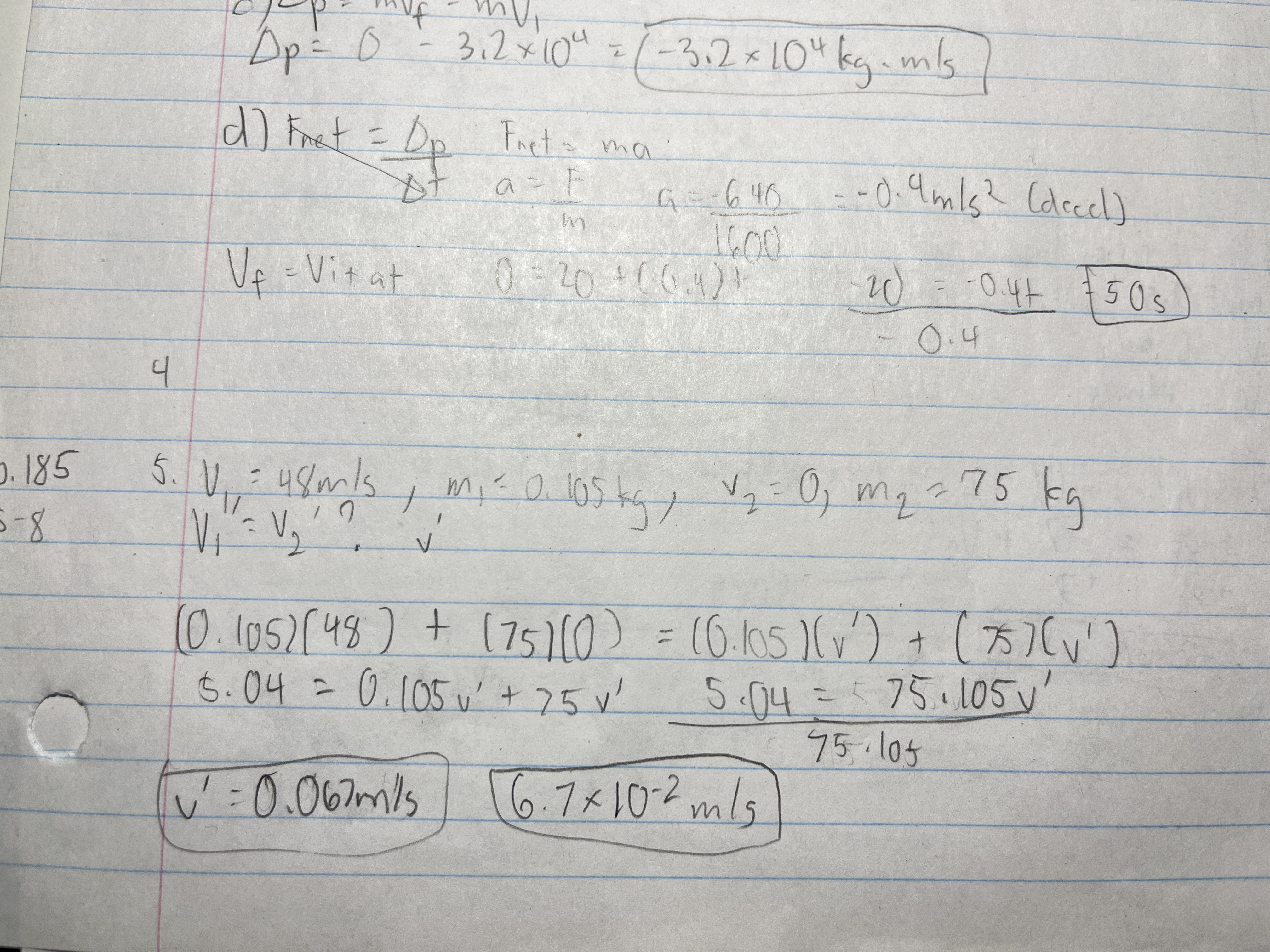
A 35.0 g bullet strikes a 5.0 kg stationary wooden block and embeds itself in the block. The block and bullet fly off together at 8.6 m/s. What was the original velocity of the bullet?

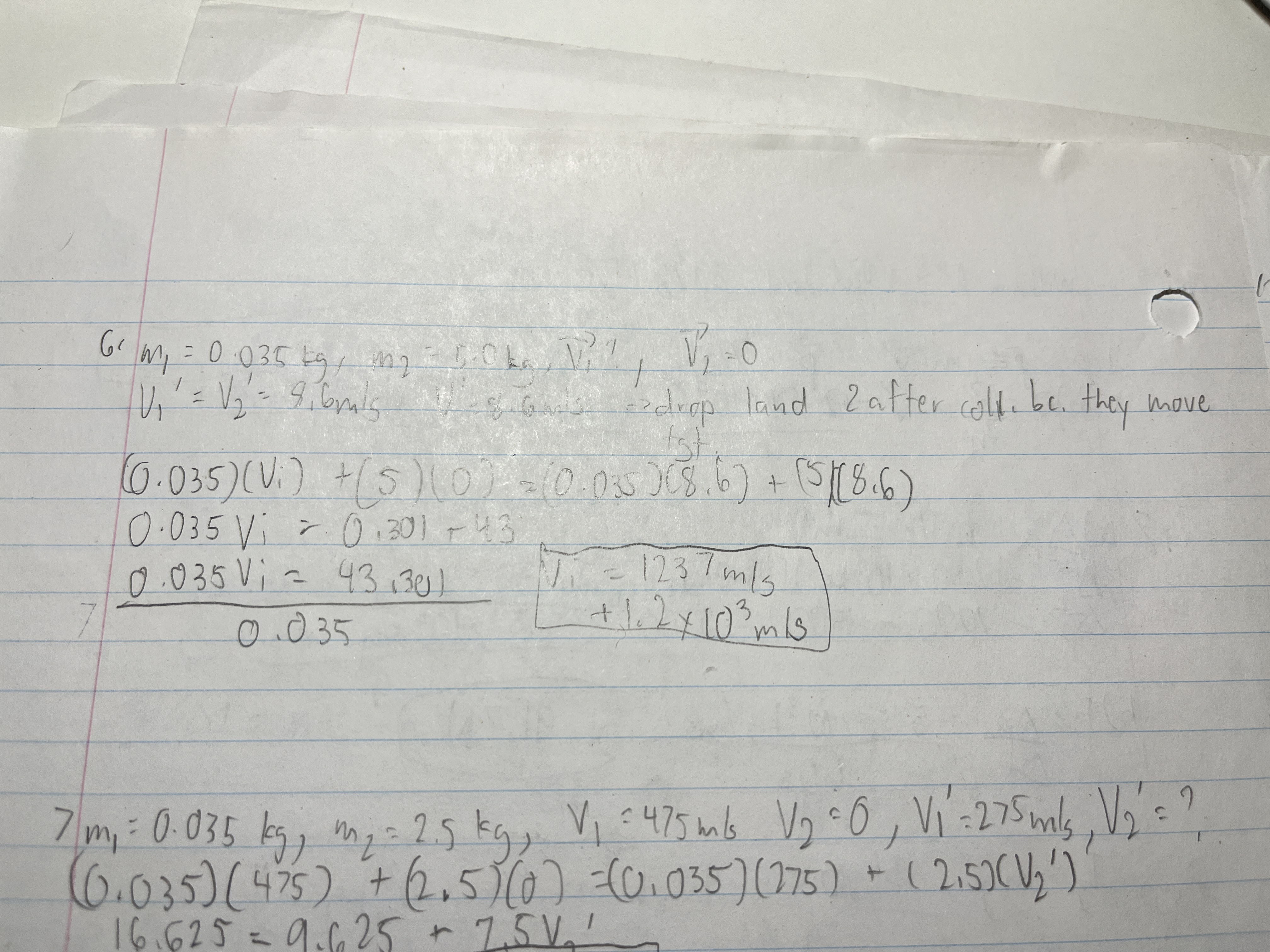
A 35.0 g bullet moving at 475 m/s strikes a 2.5 kg wooden block. The bullet passes through the block, leaving at 275 m/s. The block was at rest when it was hit. How fast is it moving when the bullet leaves?

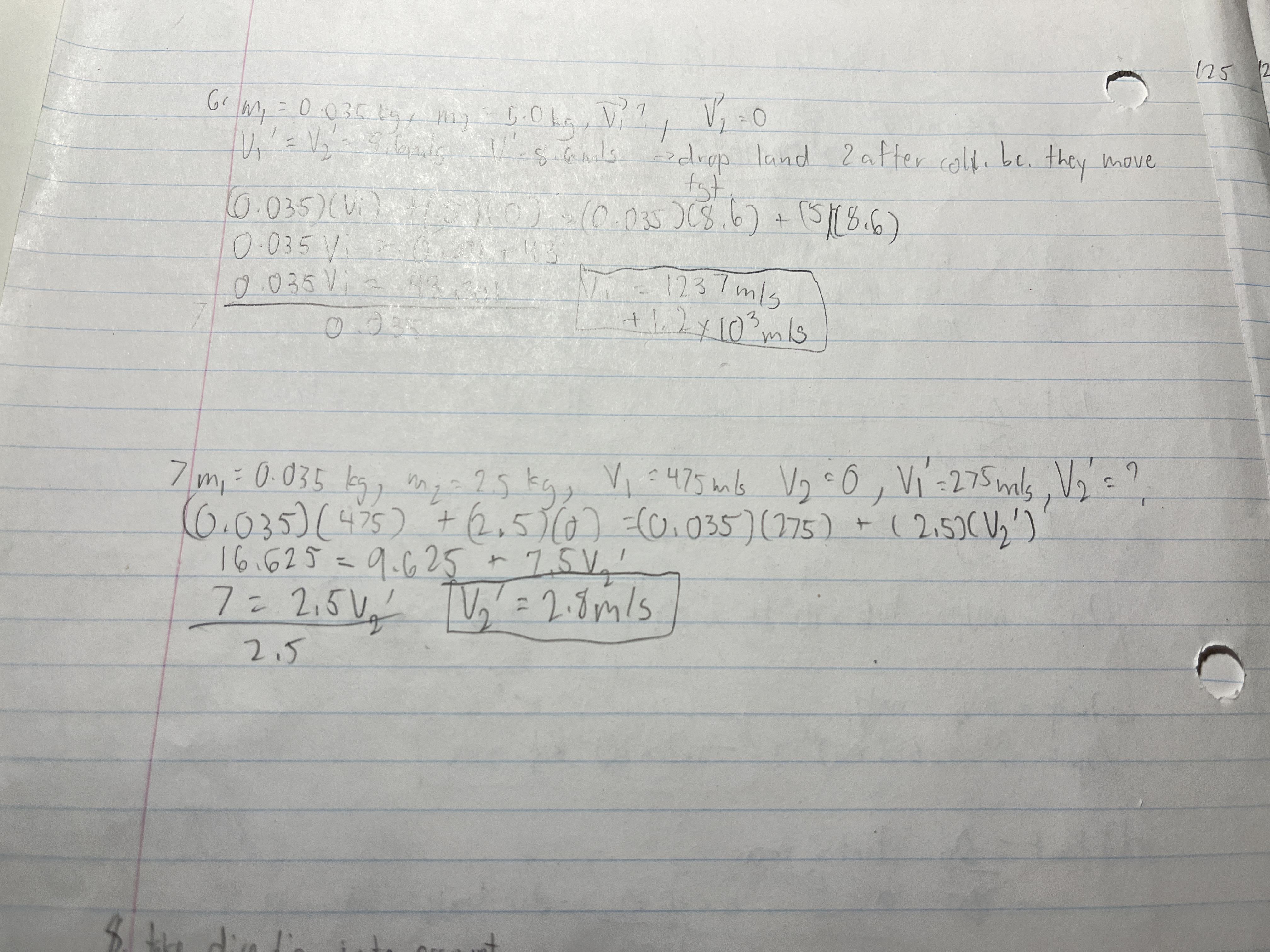
A 0.50 kg ball traveling at 6.0 m/s collides head-on with a 1.00 kg ball moving in the opposite direction at a velocity of -12.0 m/s. The 0.50 kg ball moves away at -14 m/s after the collision. Find the velocity of the second ball.

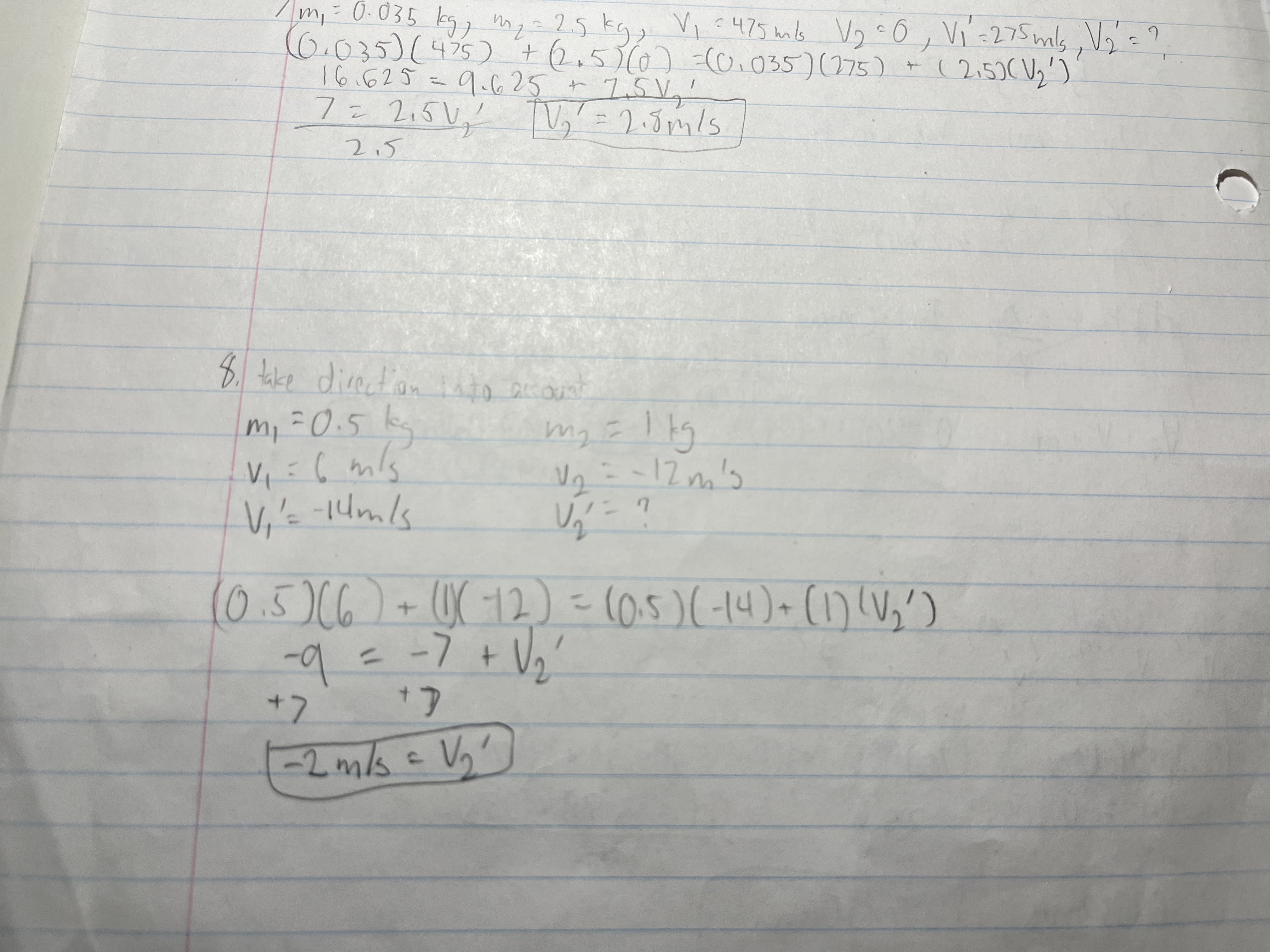
A 4.00 kg model rocket is launched, shooting 50.0 g of burned fuel from its exhaust at an average velocity of 625 m/s. What is the velocity of the rocket after the fuel has burned? (Ignore effects of gravity and air resistance)

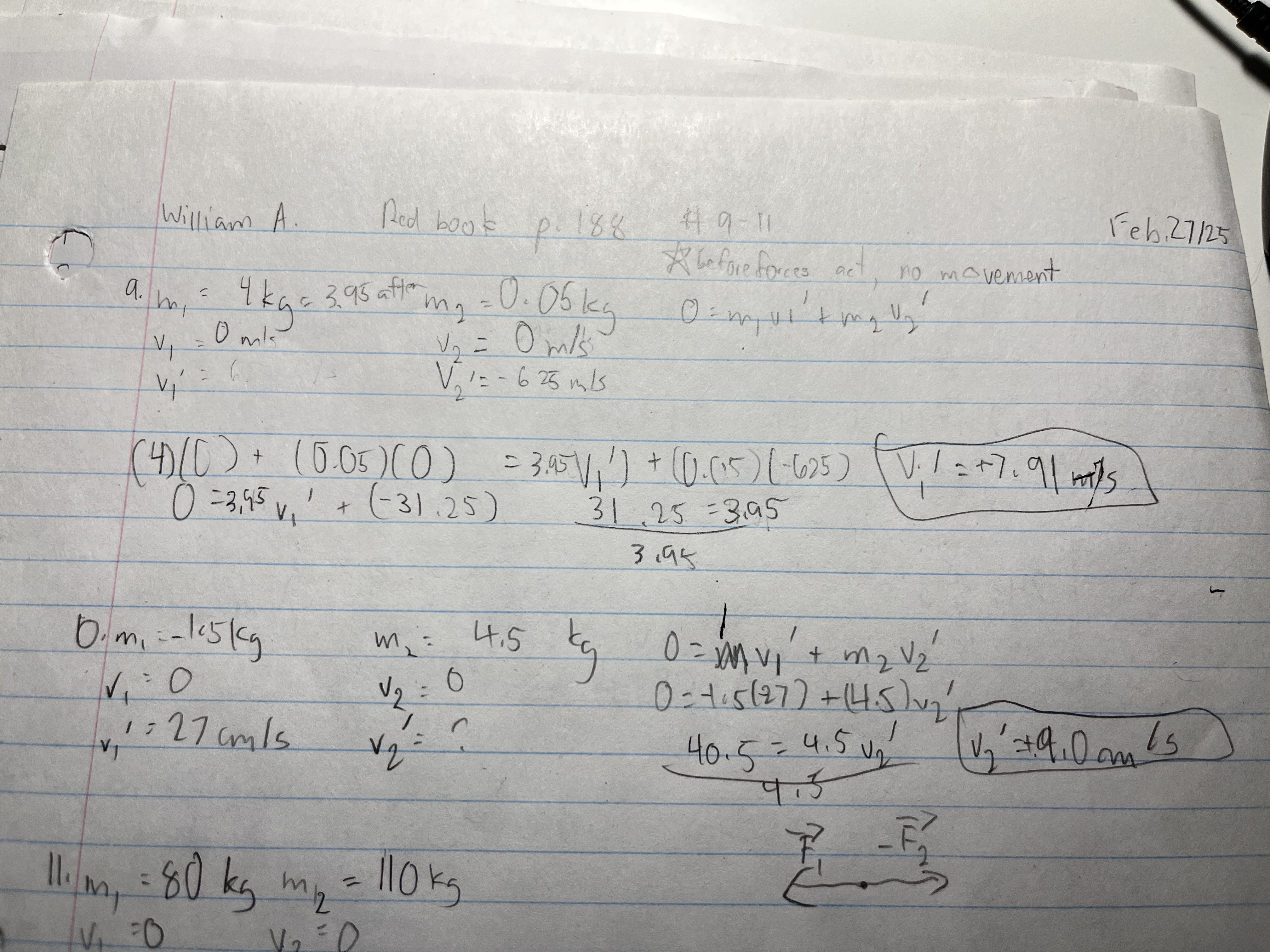
A thread holds two carts together on a frictionless surface. A compressed spring acts upon the carts. After the thread is burned, the 1.5 kg cart moves with a velocity of 27 cm/s to the left. What is the velocity of the 4.5 kg cart?

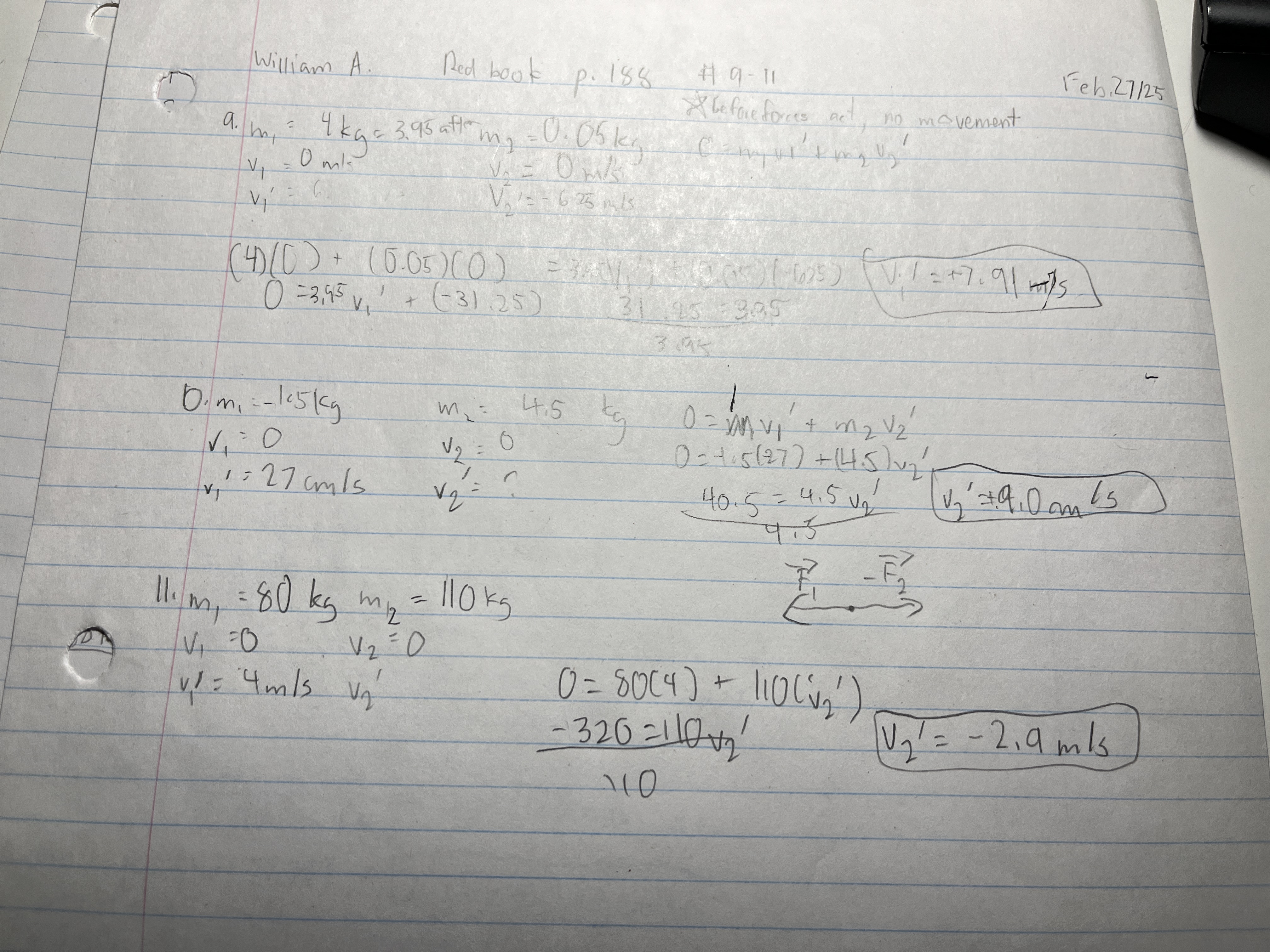
Two campers dock a canoe. One camper steps onto the dock. This camper has a mass of 80.0 kg and moves forward at 4.0 m/s. With what speed and direction do the canoe and the other camper move if their combined mass of 110 kg?

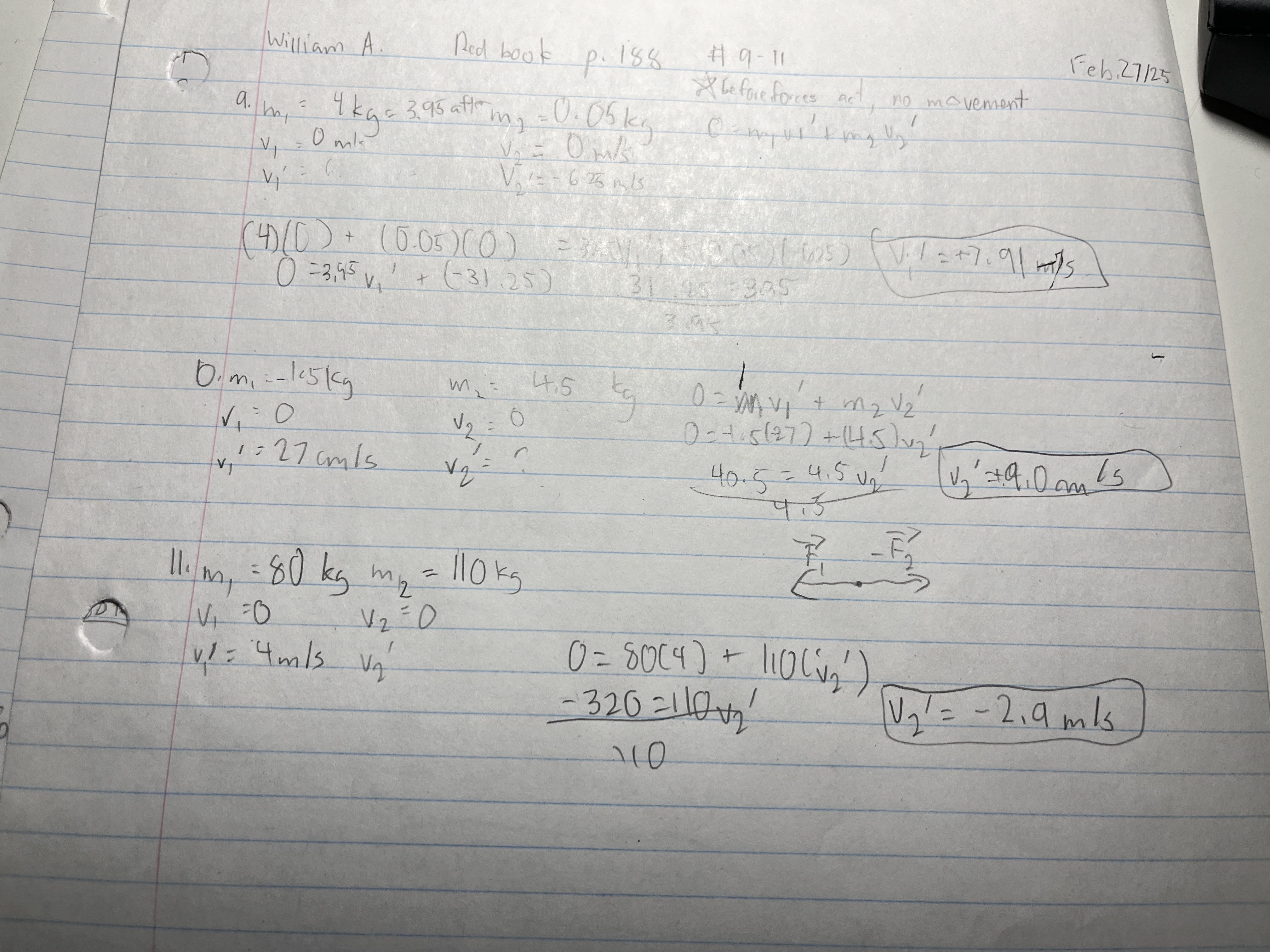
A hockey player makes a slap shot, exerting a force of 30.0 N on the hockey puck for 0.16 s. What impulse is given to the puck?

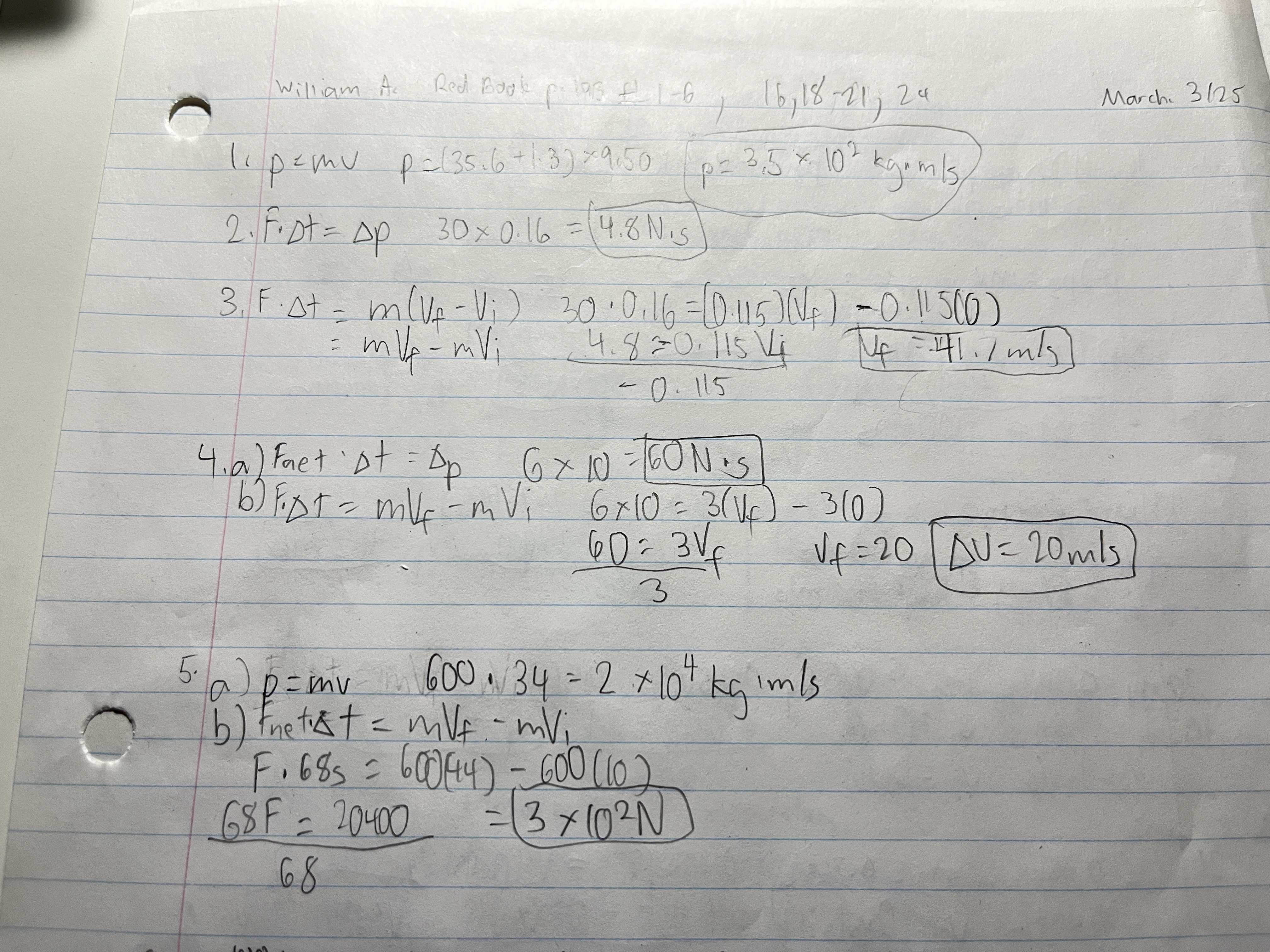
p.193 - 1.Jenny has a mass of 35.6kg and her skateboard a mass of 1.3kg. What is the momentum of jenny and her skateboard together if they are going 9.50m/s?

You first have to add the masses together to get the total mass, then multiply it by the velocity.

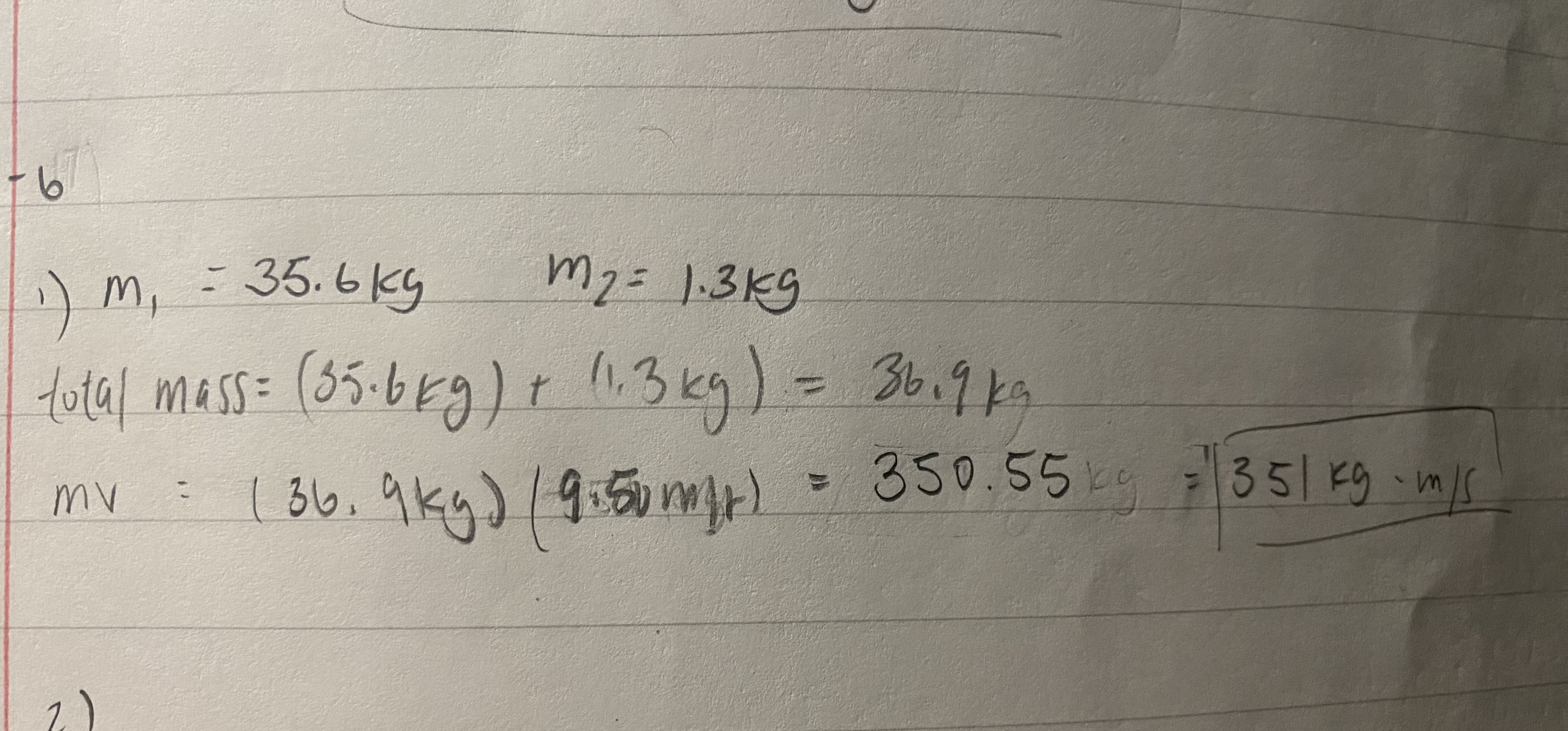
p. 194 - 16) A 95kg fullback, running at 8.2m/s, collides in midair with a 128kg defensive tackle moving in the opposite direction. Both players end with 0 speed.

a) What was the fullback’s momentum before the collision?

The fullback's momentum before the collision is calculated by multiplying his mass by his velocity, resulting in 779 kg·m/s.

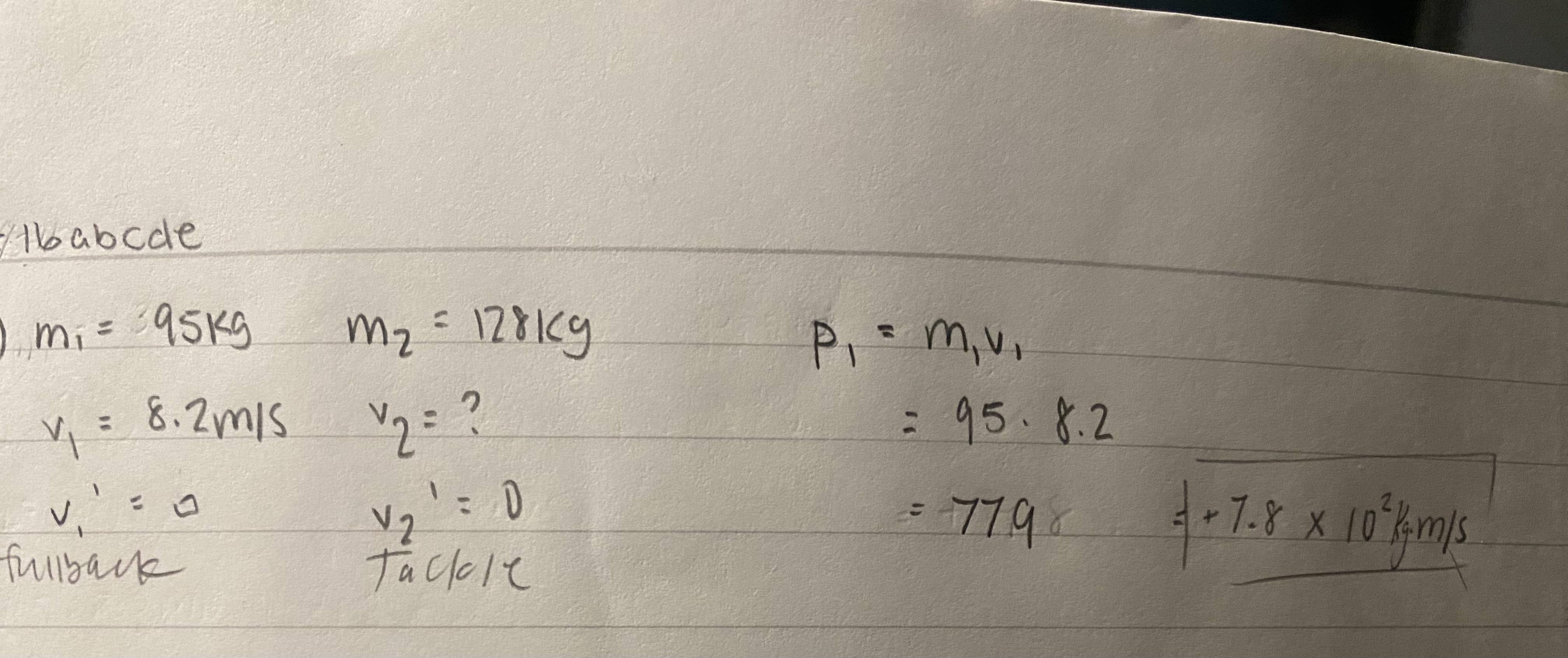
b) what was the change in the fullback’s momentum?

The change in the fullback's momentum is equal to his initial momentum since he comes to a stop, ending up with a change of -7.8 × 10² kg·m/s.

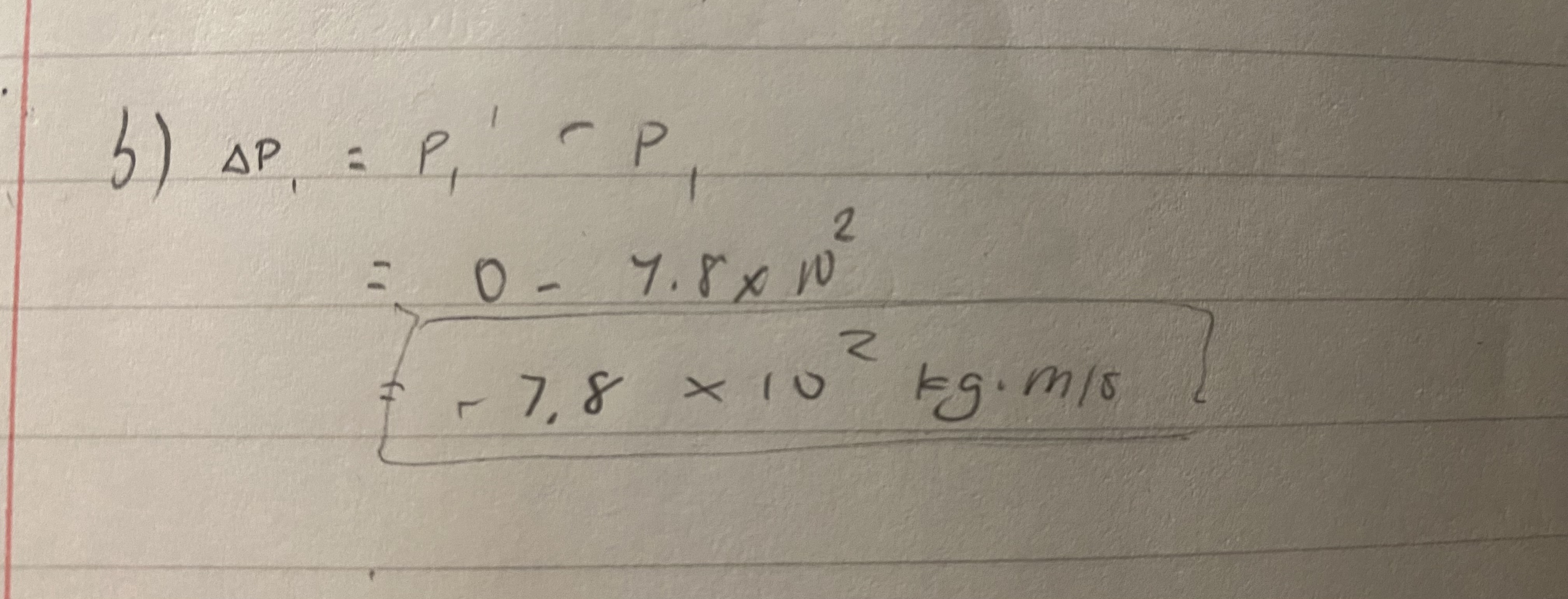
c) what was the change in the tackle’s momentum?

The tackle’s change in momentum is P2 and it is equal to -change in P1 so the tackle’s momentum change is +7.8 × 10² kg·m/s.

A 2575-kg van runs into the back of a 825-kg compact car at rest. They move off together at 8.5 m/s. Assuming no friction with the ground, find the initial speed of the van.

This problem involves the conservation of momentum, where the total momentum before the collision equals the total momentum after the collision. The initial speed of the van can be calculated using the formula: (mass of van * initial speed of van) = (mass of van + mass of car) * final speed.

A 15-g bullet is shot into a 5085-g wooden block standing on a friction-less surface. The block, with the bullet in it, acquires a velocity of 1.0 m/s. Calculate the velocity of the bullet before striking the block.

This problem also utilizes the conservation of momentum principle, whereby the momentum of the bullet before the collision equals the combined momentum of the bullet and block after the collision. The initial velocity of the bullet can be found using the formula: (mass of bullet * initial speed of bullet) = (mass of bullet + mass of block) * final speed.

A hockey puck, mass 0.115 kg, moving at 35.0 m/s, strikes a rubber octopus thrown on the ice by a fan. The octopus has a mass of 0.265 kg. The puck and octopus slide off together. What is their velocity?

This scenario also demonstrates the conservation of momentum, where the momentum of the puck before the collision equals the momentum of the puck and octopus after they collide and move together. The final velocity can be calculated using the formula: (mass of puck * initial speed of puck) = (mass of puck + mass of octopus) * final speed.

A car with mass 1245 kg, moving at 29 m/s, strikes a 2175-kg car at rest. If the two cars stick together, with what speed to they move?

This problem involves the conservation of momentum, where the momentum of the moving car before the collision equals the momentum of both cars after they collide and move together. The final speed can be calculated using the formula: (mass of first car * initial speed of first car) = (mass of first car + mass of second car) * final speed.