AP Calculus AB Flashcards

Add on as you learn more!

Another way to write csc(x)

1/sin(x)

Another way to write sec(x)

1/cos(x)

Another way to write cot(x)

1/tan(x) or cos(x)/sin(x)

f(x) is continuous at x = c if what 3 things happen?

1) lim_x→c f(x) exists

2) f(c) is defined

3) lim_x→c f(x) = f(c)

When taking limits as x→∞ or x→-∞, the y-values approach the….

Horizontal Asymptote (HA)

BOBO (Bigger on bottom, HA = 0)

BOTN (Bigger on top, NO HA)

EATS DC (Exponents are the same, divide coefficients)

lim_x→0 sin(x)/x =

1

lim_x→0 1 - cos(x)/x =

0

Intermediate Value Theorem - IVT (verbally and graphically)

If f(x) is continuous on the closed interval [a,b] and c is in that interval, the IVT guarantees that f(c) is also in between f(a) and f(b).

Point-Slope Form of a line

y - y₁ = m(x - x₁)

Limit Definition of the Derivative

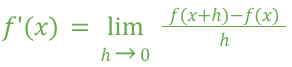
d/dx[ln(x)] =

1/x

d/dx[e^x] =

e^x

d/dx[√x] =

1/2√x

d/dx[a^x] =

a^xln(a)

d/dx[sin(x)] =

cos(x)

d/dx[cos(x)] =

-sin(x)

d/dx[tan(x)] =

sec²(x)

d/dx[sec(x)] =

sec(x) * tan(x)

d/dx[csc(x)] =

-csc(x) * cot(x)

d/dx[cot(x)] =

-csc²(x)

d/dx[xⁿ] =

nx^n-1

d/dx[f(x) * g(x)] =

f(x) * g’(x) + f’(x) * g(x)

d/dx[f(x)/g(x)] =

(g(x) * f’(x) - f(x)