LC MATHS: LINE- AXIOMS & THEOREMS

Axiom definition

statement in maths that we assume to be true

Axiom 1: Two point axiom

there is exactly 1 LINE through two given points

Axiom 2: Ruler axiom

properties of the distance between 2 points:

• the distance between two points |AB| can never be negative

• |AB|=|BA|, the distance is affected by direction

• |AB|= |CB|+|AC|, distance is preserved through addition

• every line can end, the distance will always be = k

Axiom 3: Protactor Axiom

• angle is always between 0-360°

• ordinary angle is always less than 180°

• straight angle is 180°

Axiom 4: Conditions of congruent triangles

• SSS

• ASA

• SAS

• RHS

CONGRUENCY DEFINITION

when 2 triangles are identical in every way except the way they lay on the page

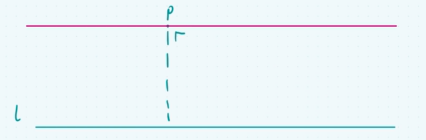
Axiom 5: Axiom of parallels

give any line l and a point P, that is exactly one line through P that is exactly parallel to l

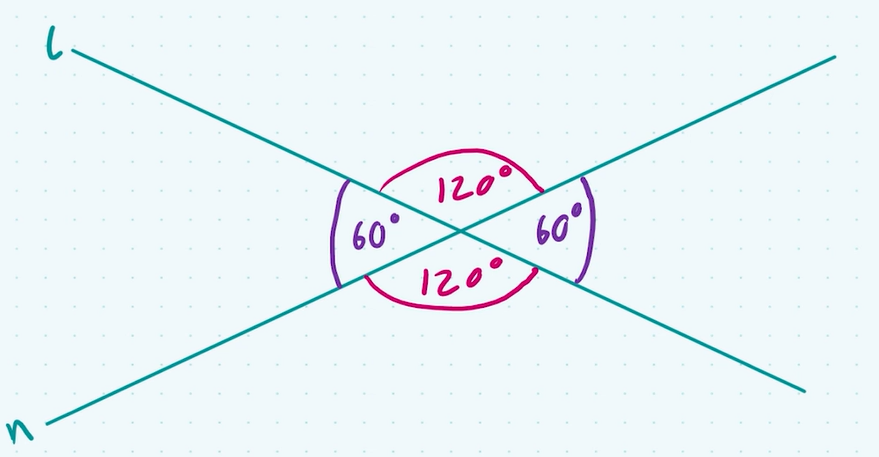
theorem 1: vertically opposite angles

are equal in measure

theorem 2: isosceles triangles

the angles opposite the equal sides are equal

ways you can prove triangle is isosceles

1. drawing a line

2. creating two congruent triangles

3. saying “since these two halves are congruent → this side = that side → triangle is isosceles.”

whats a transversal line?

a line that cuts other lines

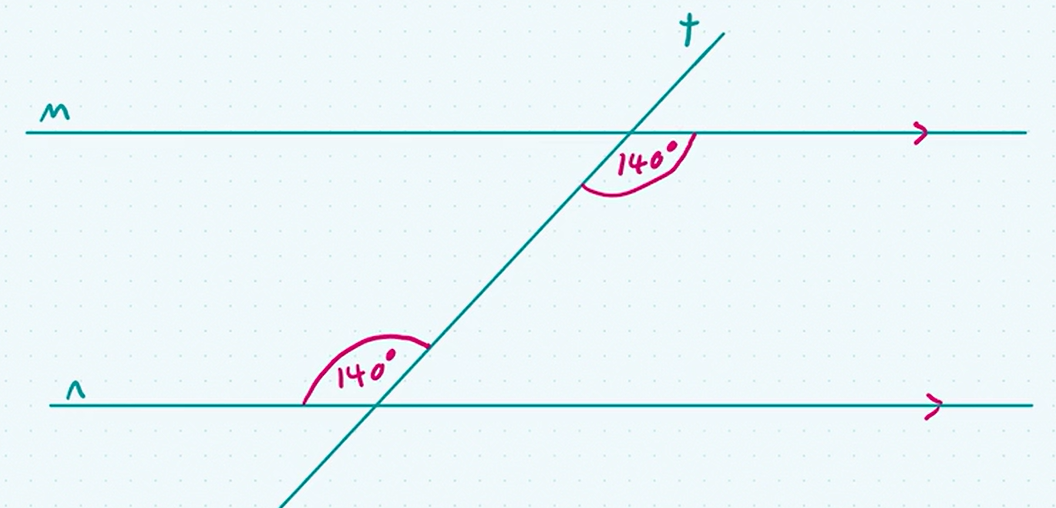
theorem 3: alternate angles

if a transversal makes equal alternate angle on two lines, then the lines parallel

theorem 4: triangle angle sum

add to 180°

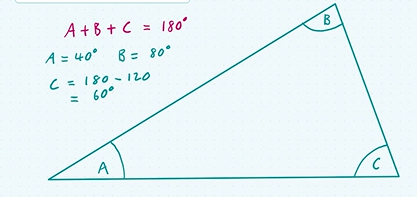
theorem 5: corresponding angles

two lines are parallel, if and only if, for any transversal the corresponding angles are equal

the phrase “if and only if”

works in both directions

theorem 6: exterior angle theorem

each angle of a triangle is equal to the sum of the interior opposite angles

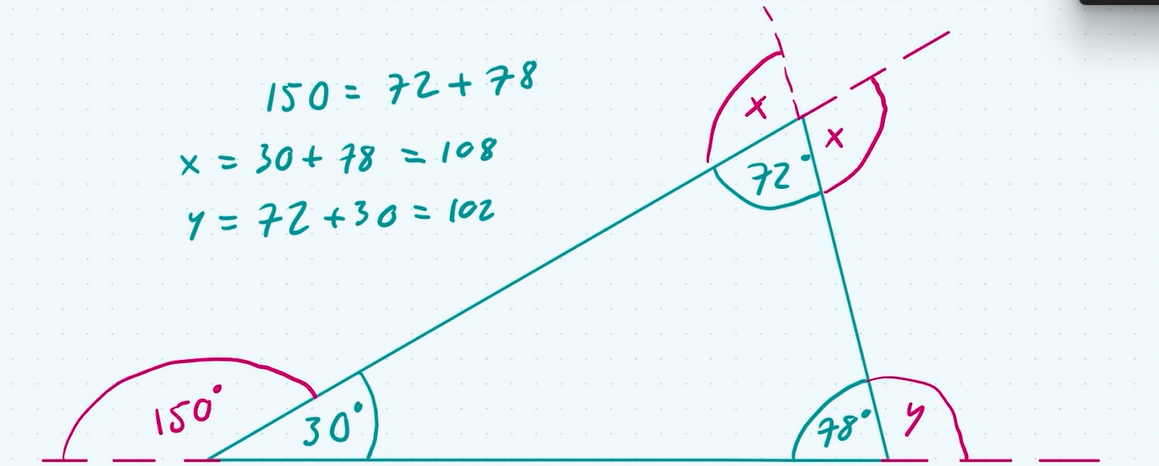
theorem 7: greater side, greater angle

in a triangle the angle opposite the two greater sides is greater than the angle opposite the lesser sides

theorem 8: Triangle inequality

two sides of a triangle are greater than the third side

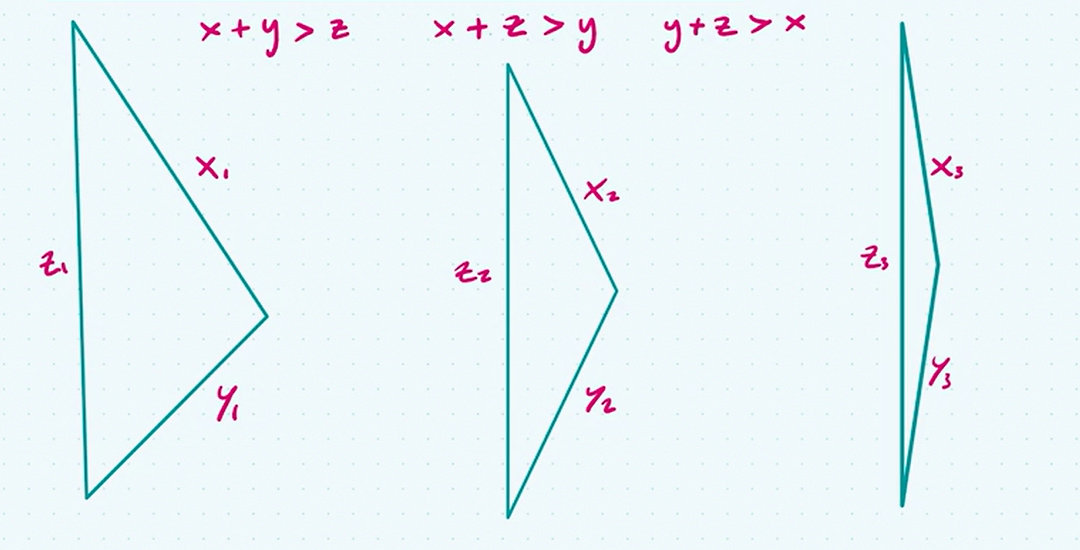
paralellogram definition

any four sided quadrilateral that is closed (convex) in which opposite sides are parallel

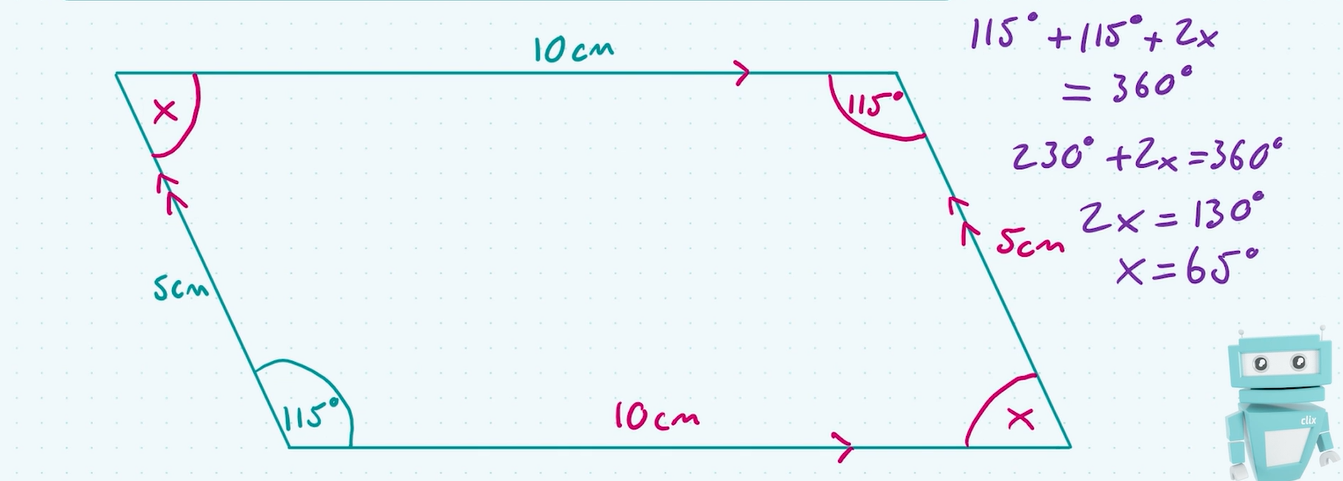
Theorem 9:opposite sides, angles in a parallelogram

opposite sides, opposite angles are equal. conversely, if opposite side and opposite angles of a convex quadrilateral are equal, it is a parallelogram

collary definition

statement which follows on from a theorem

corollary 1 (based on theorem 9)

a diagonal divides a parallelogram into two congruent triangles

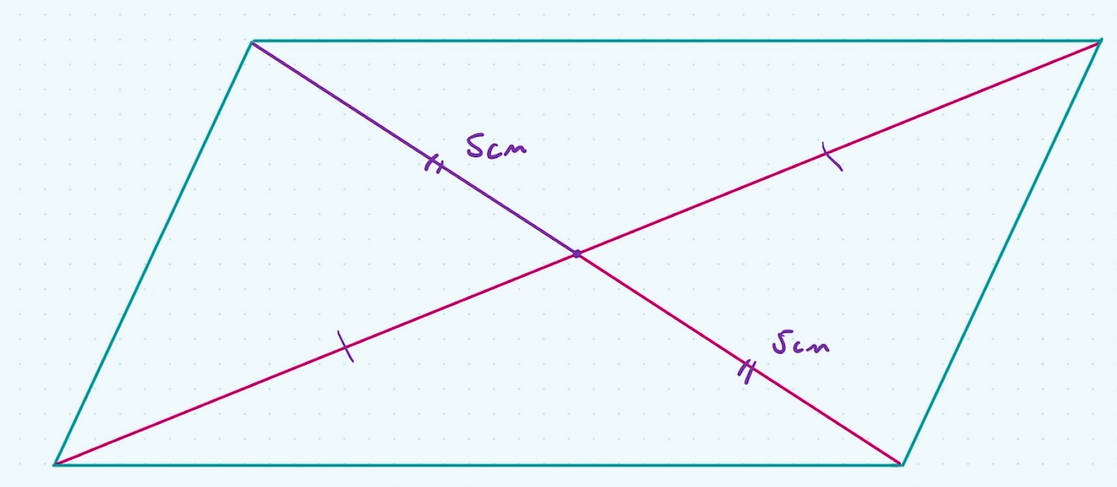
theorem 10: diagonals of a parallelogram

diagonals of a parallelogram bisect each other

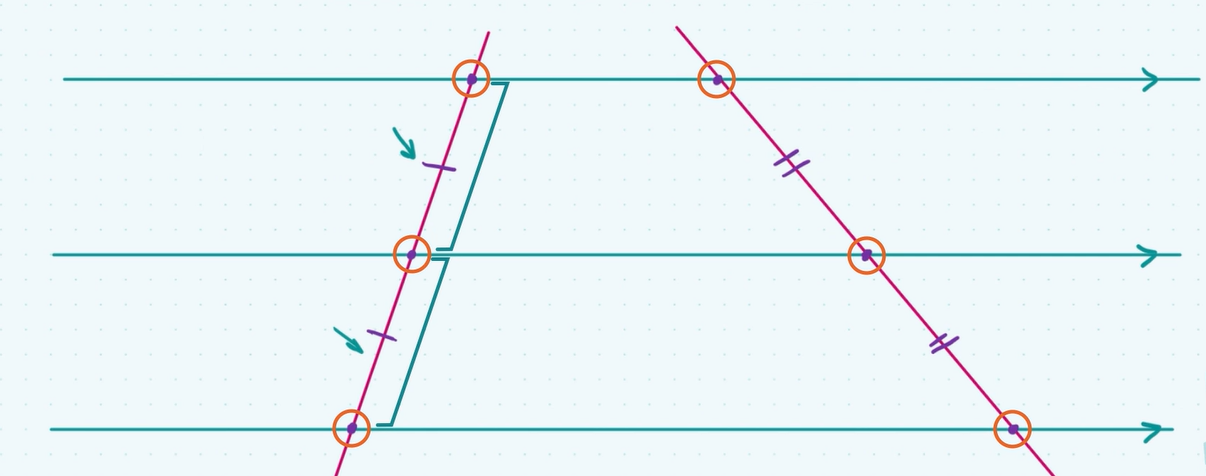
theorem 11: equal segments of a transversal

if 3 parallel lines cut off equal segments on some transversal line, then they will cut off equal segments on any other transversal

bisect meaning

cut in half