Relations and Functions, and Patterns and Numbers in Nature and the World

Relation

the relationship between two or more variables (Ex. Mother and Child, Salary and Hours, Height and Weight).

C.S. Peirce

introduced the formal definition of relation.

One-to-one

What type of relation is this?

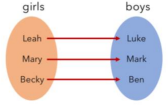
Many-to-one

What type of relation is this?

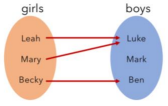
One-to-many

What type of relation is this?

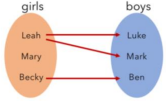
Function

A relation between a dependent and independent variable/s where in for every value of the IV (x or input), there exists a unique or a single value of the dependent variable (y or output).

Fibonacci Sequence

You can see this sequence in the spiral pattern of seeds in the head of a sunflower and these are very number numbers existing in a sequence.

Fractals

Geometric shapes that repeat their structure on ever-fine scales.

Mathematics

developed by human mind and culture, is a formal system of thought for recognizing, classifying, and exploiting patterns.

Ian Stewart

He defined the word “Mathematics”.

Logic

Science of correct thinking and reasoning. It is an interdisciplinary field which studies truth and reasoning.

Socrates (400 BC, Greece)

Philosopher and Father of critical thinking

Gottfried Wilhelm Leibnitz (1646-1716)

German mathematician who combined logic and math to create symbolic language that can solve scientific problems.

Augustus de Morgan (1806-1871)

British logician and mathematician who viewed math as an abstract study of symbols.

George Boole (1815-1864)

English mathematician and Father of symbolic logic , used several symbols to represent simple statements and connectives.

Charles Lutwidge Dodgson (1832-1898)

English writer and “mathematician” known as Lewis Carroll who wrote nonsensical classics such as Alice Adventures in Wonderland Through the Looking Glass.

Statement

it is a declarative sentence that is either true or false, but not both.

Simple Statement

a proposition/statement that conveys a single idea.

Compound Statement

a proposition/statement that conveys two or more ideas.

Existential quantifiers

Used as prefixes to assert the existence of something (e.g. “there exists” and “at least one”).

Universal quantifiers

deny the existence of something (e.g. none, no) and used to assert that every (or all) element of a given set satisfies some condition.

Tautology

a proposition (statement) that is always true, regardless of the truth values of the propositional variables it contain.

Contradiction

A proposition/statement that is always false.

Contingency

A proposition/statement that is neither true or false.

Conditional statement

Identify the kind of statement

Converse

Identify the kind of statement. It is written in the form q → p.

Inverse

Identify the kind of statement. It is written in the form ~p → ~q.

Contrapositive

Identify the kind of statement. It is written in the form ~q → ~p.

Biconditional

Identify the kind of statement. It is written in the form p < - > p.