5 - Waves and Sound (fuck magnetism)

F = -kx

F = restoring force (back to equilibrium)
k = spring constant [k] = N/m
x = displacement from EQ

hooke’s law formula

simple harmonic function

back and forth motion (ex: waves, sound, spring, etc.)

PE_elastic = (1/2)kx² OR E_total = (1/2)kA²

A = amplitude (in case displacement is not used)

formula for nrg stored in spring as it stretches/compresses (potential energy)

W_{by spring} = -ΔPE_elastic = -(1/2)kx²

ALL Work formulas are ±PE

formula for work by the spring (hint: it’s a conservative force)

period (T)

the time it takes to complete 1 cycle (returns to same position and velocity)

frequency (f)

f = 1/T → in Hertz (Hz = 1/second)

number of cycles in ONE second (1/second = Hz)

f = 1/T in hertz

simple harmonic motion frequency formula

waves

propagating oscillations that transfers nrg

1. medium is not propagating with the energy

   1. medium oscillates with a series of identical oscillations slightly out of phase

particles oscillate in mechanical waves. Whereas electric & magnetic fields oscillate in EM waves

difference between mechanical and EM wave?

1. wavelength (λ): length of 1 cycle (crest → crest; trough → trough)

2. amplitude (A): max displacement of medium from EQ

3. wave speed (v): speed of wave moving to the right (d = vt)

4. period (T): time for 1 cycle to go by, or for 1 particle to finish 1 oscillation

5. frequency (f): # of pulse that passes per second

5 properties of waves:

wavelength (λ)

length of 1 cycle (crest → crest; trough → trough)

amplitude (A)

max displacement of medium from EQ

wave speed (v)

speed of wave moving to the right (d = vt)

period (T)

time for 1 cycle to go by, or for 1 particle to finish 1 oscillation

frequency (f)

# of pulse that passes per second

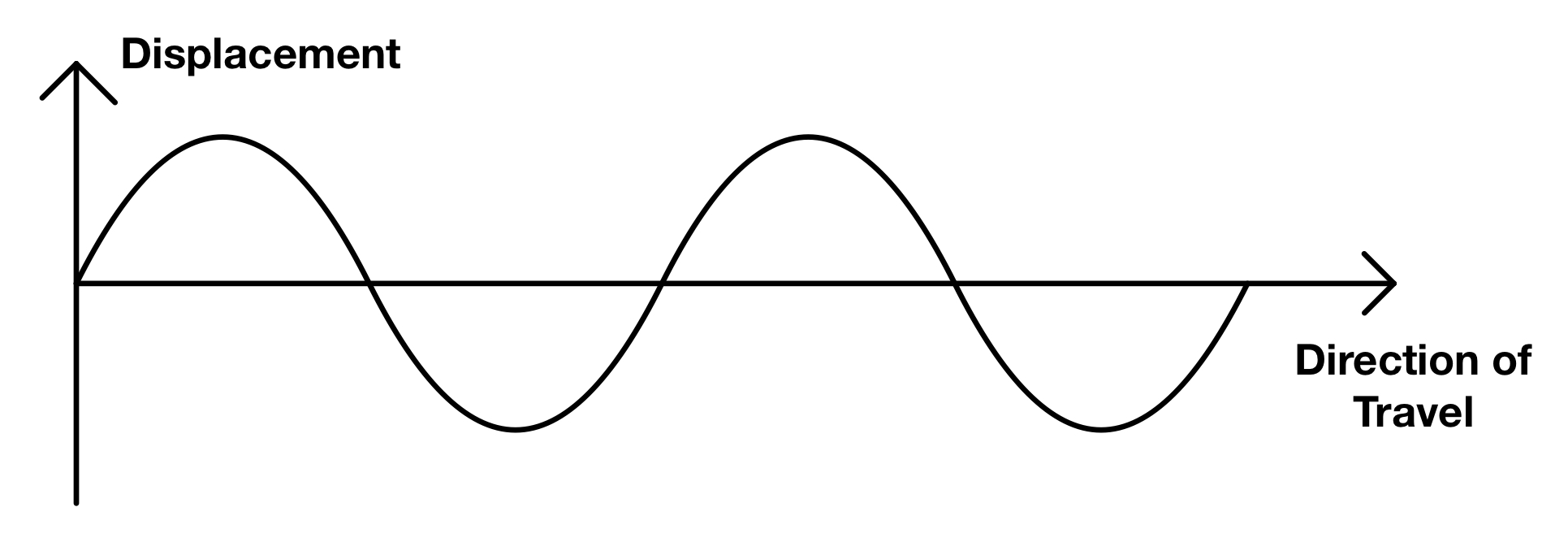
transverse waves

type of wave where medium oscillates that’s perpendicular to the direction of wave propagation (ex: ocean waves, waves on string, EM wave)

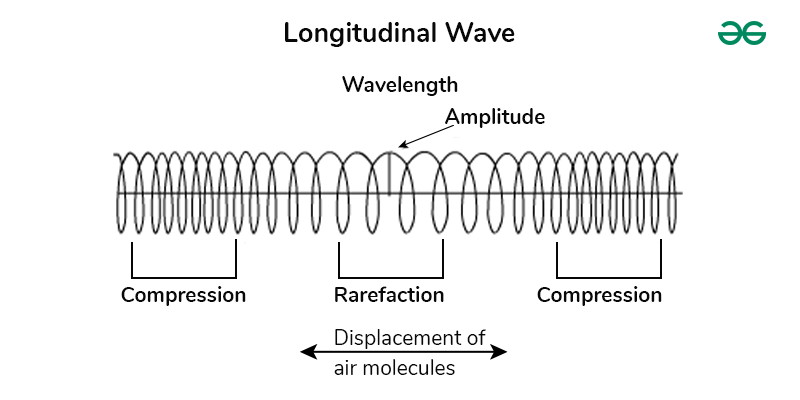
longitudinal wave

type of wave where medium oscillates parallel to the direction of wave propagation (ex: sound)

v = λf

formula for speed (v) using wavelength (λ) and frequency (f)

type of wave, physical properties of medium

speed of a wave (v) depends on:

1. ______________ of wave

2. ______________ of medium

frequency

a wave moving from 1 medium to another will maintain its ______________

velocity (v)

_____________ is constant in a medium, regardless of the frequency or length of it

gas, liquid, solid

sound waves travel the SLOWEST in ___________ (gas/liquid/solid) < (gas/liq/solid) < FASTEST in __________ (gas/liq/solid)

solid > liquid > gas

rank the type of medium sound waves travel the FASTEST to SLOWEST in

intensity (I)

I = Power (P) / Area (A) = W / m²

energy of a wave incident per unit area per unit time

I = Power (P) / Area (A) = W / m²

formula for intensity

doppler shift

shift in the detected frequency of wave due to relative motion between detector and sound source

1. detector and source getting closer together = higher frequency

2. detector and source getting farther = lower freq

v = 350 m/s

whats the speed of sound in air?

v = 3×10^8

what’s the speed of light wave in a medium?

f_d = f[(v ± v_D) / (v ± v_S)]

1. f_d = observed frequency

2. f = actual frequency

3. v_D = velocity of detector (hears the sound)

4. v_S = velocity of source (makes the sound)

doppler shift formula

vD = 10 m/s, vS = 20 m/s

f = 500 Hz

cyclist moving TOWARD the beep (+vD), bus moving AWAY from beep (-vS)

500(350

A cyclist is riding behind a bus, both traveling on a straight road. The bus is moving at a constant velocity of 20 m/s, and the cyclist is riding at a constant velocity of 10 m/s. The bus driver honks the horn, emitting a sound wave with a frequency of 500 Hz. If the speed of sound in air is 343 m/s, what is the frequency of the sound wave heard by the cyclist?

A) 465 Hz
B) 500 Hz
C) 535 Hz
D) 570 Hz