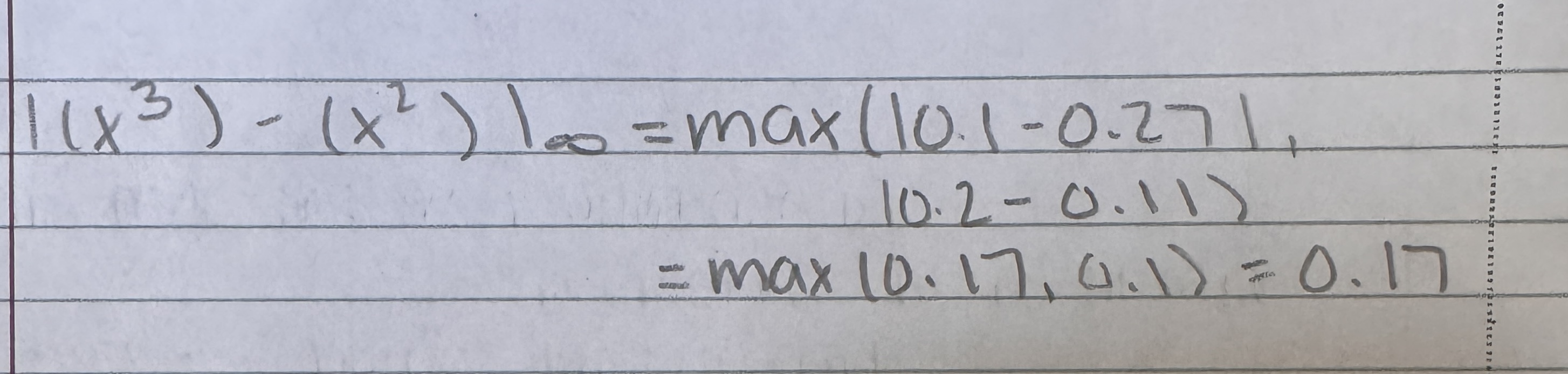Quiz 4

Cards 12-15 are the solution to the questions that you need to work out

The following matrix:

• will not require pivoting when solved by gauss elimination

• will require pivoting when solved by gauss elimination

• is not diagonally dominant

• is diagonally dominant

• will require pivoting when solved by gauss elimination

• is not diagonally dominant

When factoring the N x N matrix [A] into its upper and lower (LU) factors

• Crout’s method set the diagonal elements of [U] equal to one

• Doolittle’s method set the diagonal elements of [L] equal to one

• Cholesky’s method set the diagonal elements of [U] equal to one

• Crout’s method set the diagonal elements of [L] equal to one

• is exact for round off error

• Cholesky’s method can be applied to any metric [A] regardless of its structure

• Crout’s method set the diagonal elements of [U] equal to one

• Doolittle’s method set the diagonal elements of [L] equal to one

• is exact for round off error

If a set of simultaneous equations [A]{x}={b} is solved by an iterative and [A] is a 400 × 400 metric and if it takes K=10 iterations to converge, the then number of floating point operations taken to find the solution is estimated to be of the order of

1,600,000

Iterative methods of solution for simultaneous equations include

• successive over relaxation (SOR)

• LU decomposition

• Jacobi iteration

• Householder decomposition

• Gauss-Seidel iteration

• successive over relaxation (SOR)

• Jacobi iteration

• Gauss-Seidel iteration

The LU decomposition method applied to the linear system [A]{x}={b} is (assume that the matrix [A] is fully populated)

• is a method that takes O(N³) floating point operations to solve the system of equations for the first right hand side vector [b] and subsequently takes on O(N³) for any new right hand side vector [b]

• is an iterative operation

• is a direct method of solution

• requires finding the lower and upper factors of the matrix [A] by one of three possible choices

• is used when the coefficient matrix [A] stays constant and there are multiple right hand sides [b] to solve

• is a direct method of solution

• is used when the coefficient matrix [A] stays constant and there are multiple right hand sides [b] to solve

• requires finding the lower and upper factors of the matrix [A] by one of three possible choices

The system of equations

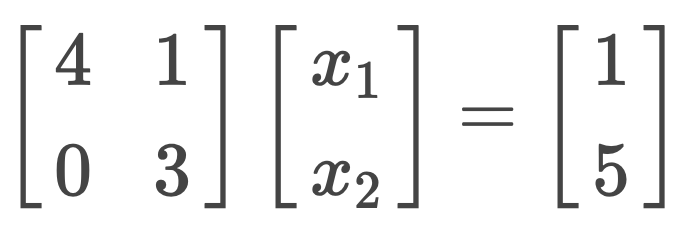
is solved by Jacobi iteration and the solution vector after the 3rd iteration is

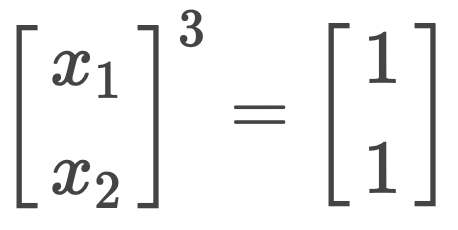
The residual norm is evaluated using L_infinity norm as

4

Faced with the following coefficient matrix of a system of equations to be solved by Gauss elimination methods, will partial pivoting be required?

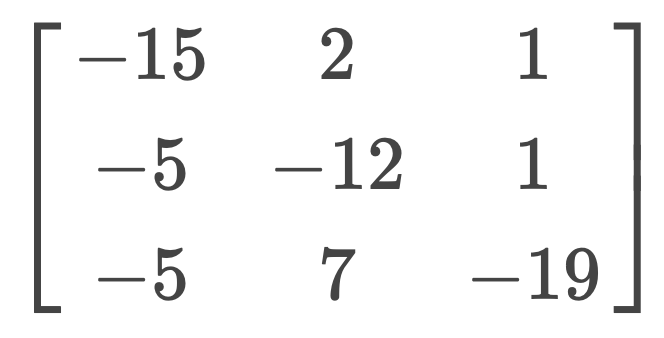
No, because the matrix is diagonally dominant

The Thomas algorithm:

• can store and solve the problem on 4 vectors

• is used to solve tridiagonal systems of linear equations

• can be applied to a set of equations with a fully populated matrix [A]

• used Crout’s method to find the factors of the coefficient matrix [A]

• is an iterative method of solution of linear systems

• is used to solve tridiagonal systems of linear equations

• can store and solve the problem on 4 vectors

• used Crout’s method to find the factors of the coefficient matrix [A]

If a set of simultaneous equations [A]{x}={b} is solved by an iterative and [A] is a 200 × 200 metric and if it takes K=10 iterations to converge, the then number of floating point operations taken to find the solution is estimated to be of the order of

400,000

When solving a linear system of equations by Jacobi iteration, given the following two vectors at iterations 2 and 3

{x}^2 = {0.27}
{ 0.1 }
{x}^3 = { 0.1 }
{ 0.2 }

using the Linf norm the iterative convergence criterion is:

0.17

The system of equations 

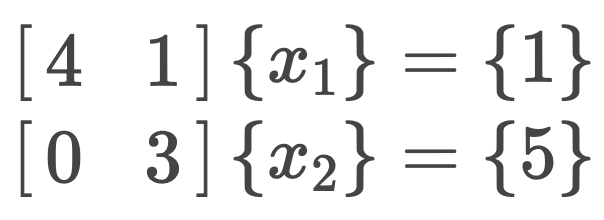
is solved by the Jacobi iteration and the solution vector after the 3rd iteration is 

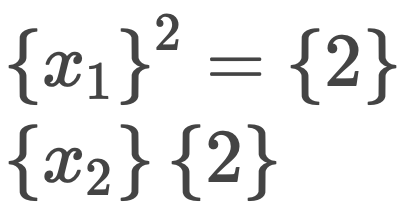
The residual norm is evaluated using the Linf norm as

9

#6 card explanation

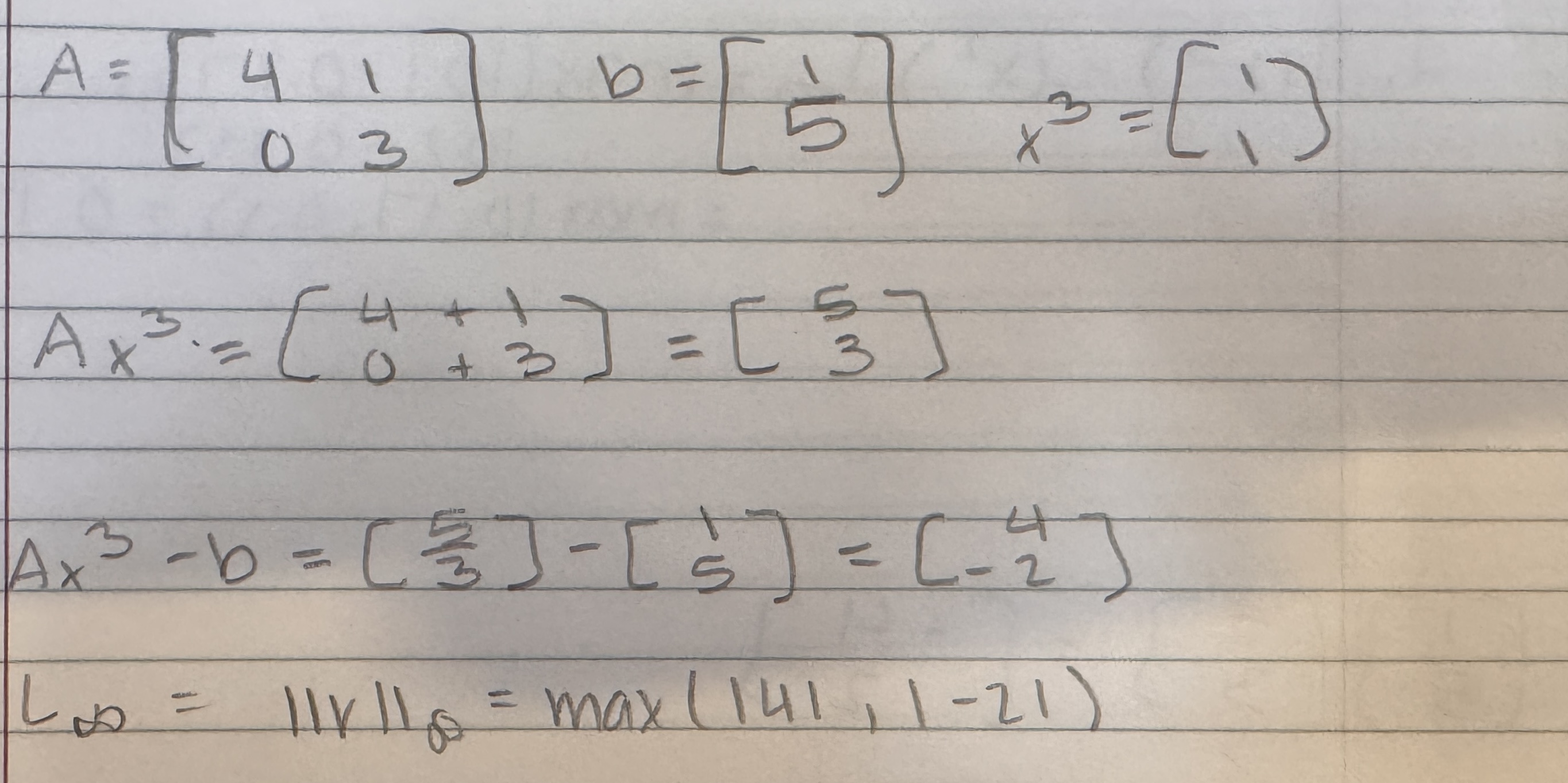
=4

#9 card explanation (applies to card #3)

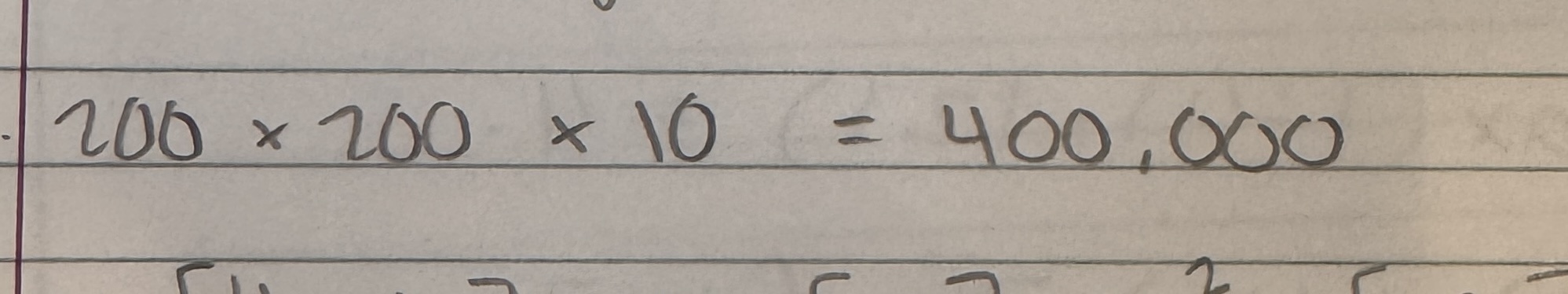
#11 card explanation

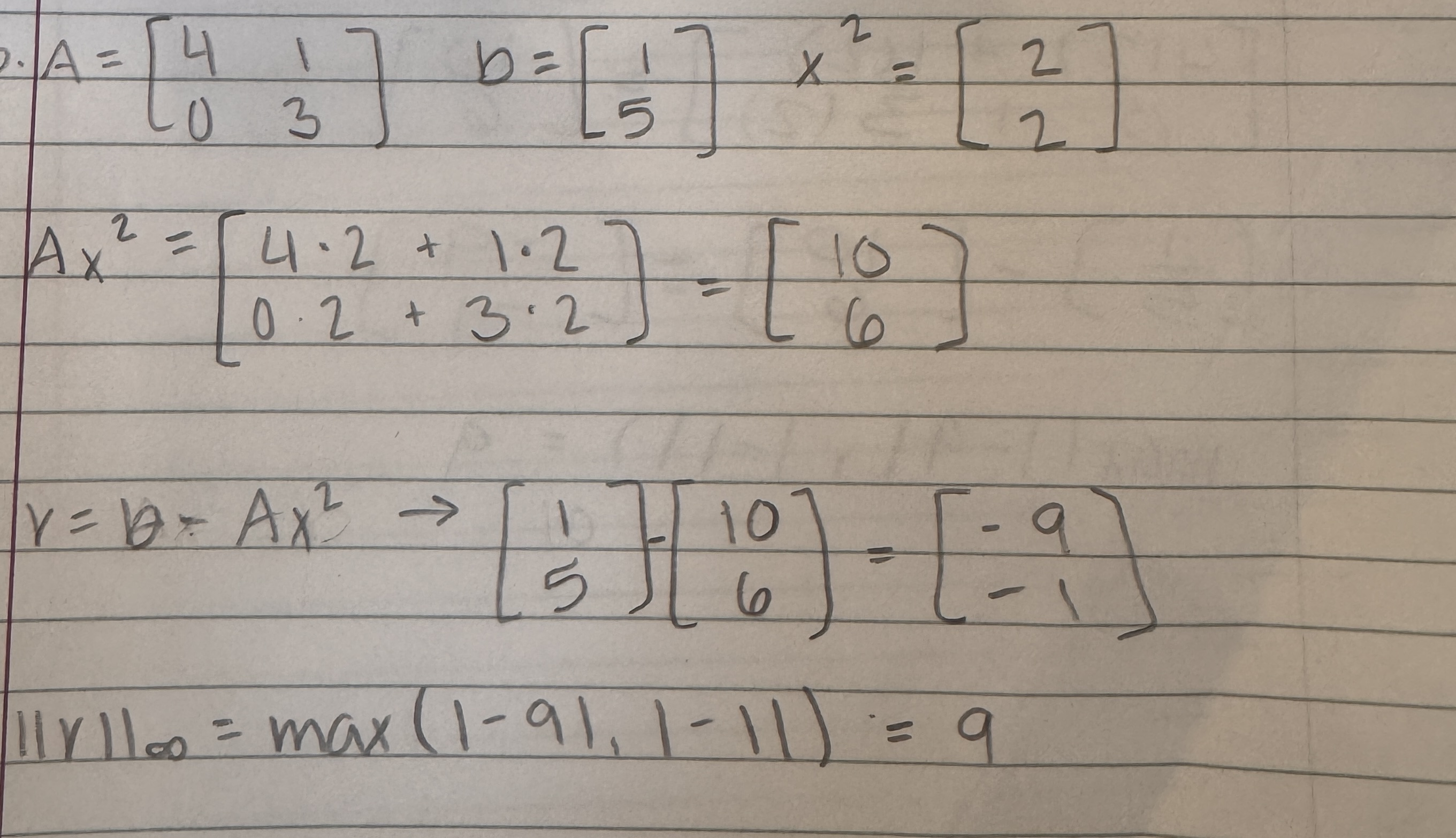
#10 card explanation