Aleks Chapter 11: States of Matter | CHEM10401

Calculating Molarity Understanding how solubility varies with temperature and pressure. Calculating Solubility Using Henry's Law to calculate the solubility of a gas. Using osmotic pressure to find molar mass.

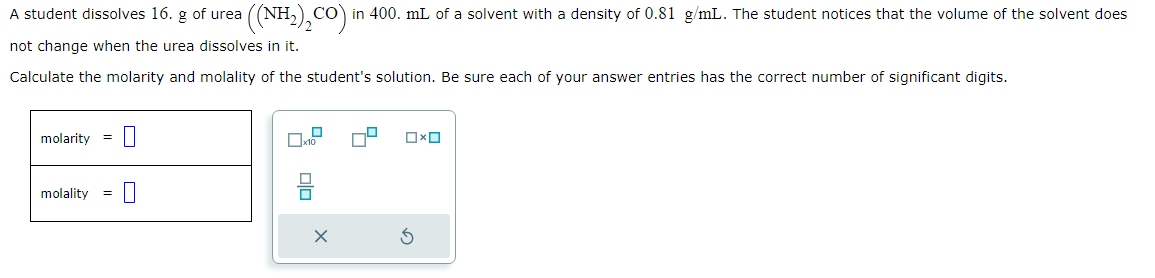
A student dissolves 16.g of urea NH22CO in 400 ml of a solvent with a density of 0.81/gmL. The student notices that the volume of the solvent does not change when the urea dissolves in it.

Calculate the molarity and molality of the student's solution. Be sure each of your answer entries has the correct number of significant digits.

A student dissolves 17. g of resveratrol (C14H12O3) in 400mL of a solvent with a density of 0.93 g/mL. The student notices that the volume of the solvent does not change when the resveratrol dissolves in it.

Calculate the molarity and molality of the student's solution. Be sure each of your answer entries has the correct number of significant digits.

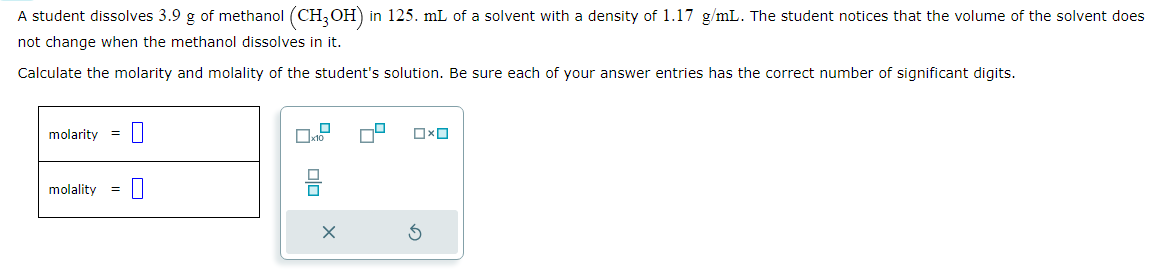
A student dissolves 3.9g of methanol (CH3OH) in 125mL of a solvent with a density of 1.17 g/mL. The student notices that the volume of the solvent does not change when the methanol dissolves in it.

Calculate the molarity and molality of the student's solution. Be sure each of your answer entries has the correct number of significant digits.

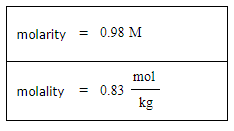
A student dissolves 12 g of phenol (C6H5OH) in 400mL of a solvent with a density of 0.89 g/mL. The student notices that the volume of the solvent does not change when the phenol dissolves in it.

Calculate the molarity and molality of the student's solution. Be sure each of your answer entries has the correct number of significant digits.

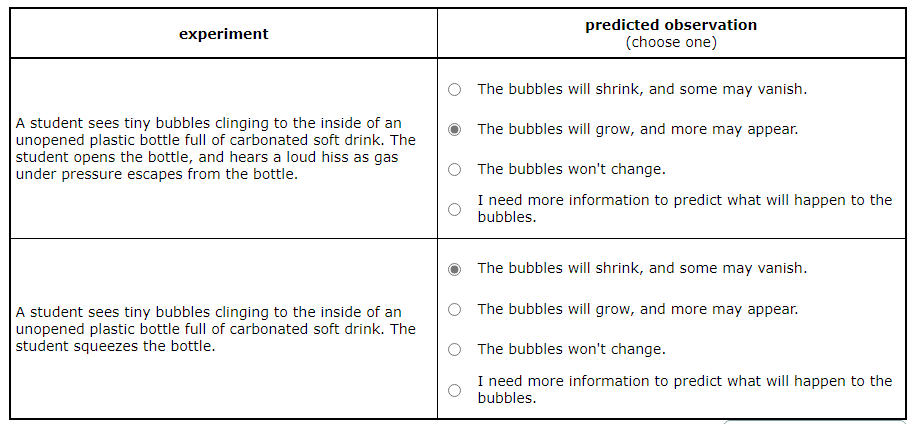
A student sees tiny bubbles clinging to the inside of an unopened plastic bottle full of carbonated soft drink. The student opens the bottle and hears a loud hiss as gas under pressure escapes from the bottle.

Predict what will be observed in the experiment.

• The bubbles will shrink, and some may vanish.

• The bubbles will grow, and more may appear.

• The bubbles won't change.

• I need more information to predict what will happen to the bubbles.

1. Opening the Bottle: When the student opens the bottle full of carbonated soft drink, the pressure inside the bottle decreases. This causes the gas that was previously dissolved in the drink under high pressure to come out of the solution, creating bubbles. So, the bubbles will grow, and more may appear.

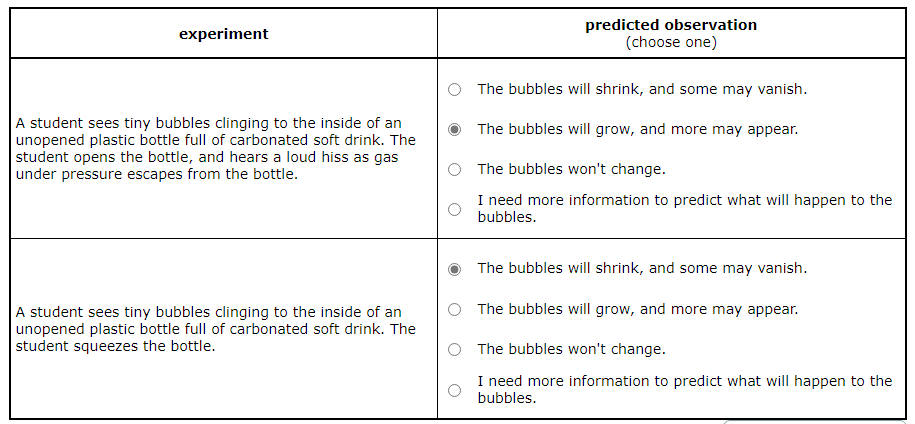
A student sees tiny bubbles clinging to the inside of an unopened plastic bottle full of carbonated soft drink. The student squeezes the bottle.

Predict what will be observed in the experiment.

• The bubbles will shrink, and some may vanish.

• The bubbles will grow, and more may appear.

• The bubbles won't change.

• I need more information to predict what will happen to the bubbles.

1. Squeezing the Bottle: When the student squeezes the unopened bottle, the pressure inside the bottle increases. This could cause the gas in the bubbles to dissolve back into the drink, making the bubbles shrink. So, the bubbles will shrink, and some may vanish.

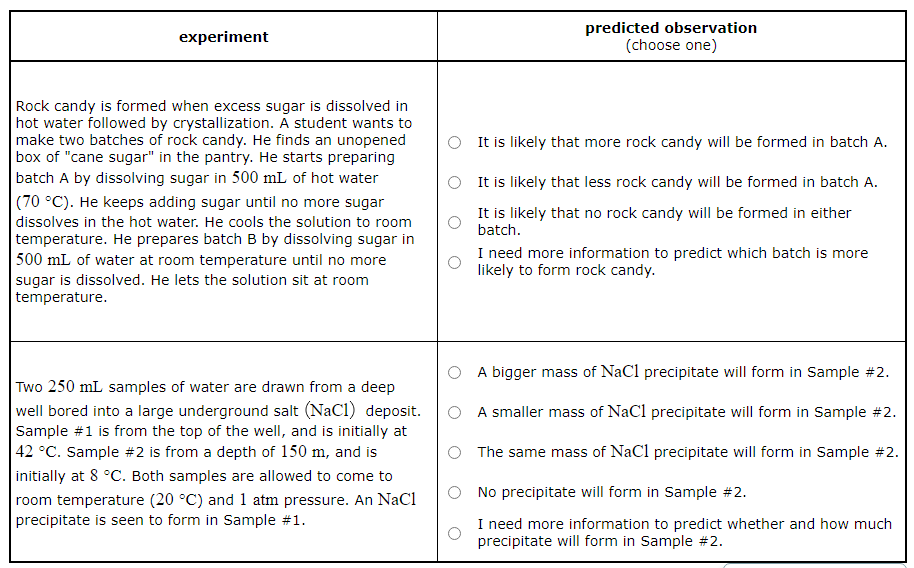
Rock candy is formed when excess sugar is dissolved in hot water followed by crystallization. A student wants to make two batches of rock candy. He finds an unopened box of "cane sugar" in the pantry. He starts preparing batch A by dissolving sugar in 500mL of hot water (70°C). He keeps adding sugar until no more sugar dissolves in the hot water. He cools the solution to room temperature. He prepares batch B by dissolving sugar in 500mL of water at room temperature until no more sugar is dissolved. He lets the solution sit at room temperature.

Predict what will be observed in the experiment.

• It is likely that more rock candy will be formed in batch A.

• It is likely that less rock candy will be formed in batch A.

• It is likely that no rock candy will be formed in either batch.

• I need more information to predict which batch is more likely to form rock candy.

1. Rock Candy Experiment: When the student prepares batch A by dissolving sugar in hot water, more sugar can be dissolved due to the increased solubility at higher temperatures. When this solution is cooled to room temperature, it becomes supersaturated, leading to the formation of more rock candy as the excess sugar crystallizes out. On the other hand, in batch B, less sugar can be dissolved at room temperature, leading to the formation of less rock candy. So, it is likely that more rock candy will be formed in batch A.

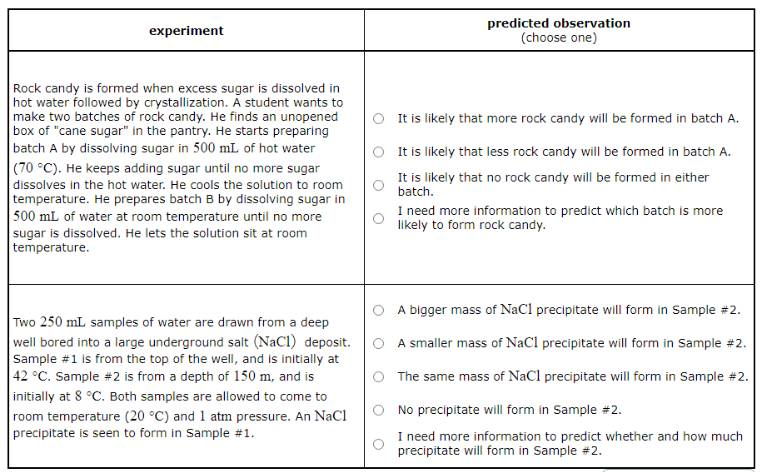
Two 250mL samples of water are drawn from a deep well bored into a large underground salt (NaCl) deposit. Sample #1 is from the top of the well, and is initially at 42°C. Sample #2 is from a depth of 150m, and is initially at 8°C. Both samples are allowed to come to room temperature (20°C) and 1atm pressure. An NaCl precipitate is seen to form in Sample #1.

Predict what will be observed in the experiment.

• A bigger mass of NaCl precipitate will form in Sample #2.

• A smaller mass of NaCl precipitate will form in Sample #2.

• The same mass of NaCl precipitate will form in Sample #2.

• No precipitate will form in Sample #2.

• I need more information to predict whether and how much precipitate will form in Sample #2.

1. Salt Deposit Experiment: As Sample #1 cools to room temperature, the solubility of NaCl decreases, leading to the formation of a precipitate. However, as Sample #2 warms to room temperature, the solubility of NaCl increases. This increased solubility allows more NaCl to dissolve and prevents the formation of a precipitate. Therefore, no precipitate will form in Sample #2.

In the second experiment, the important distinction between the samples is their initial temperatures. (The difference in initial pressure, because Sample #2 was taken from deep under the surface of the well, won't change the solubility of the solid salt.) The temperature of Sample #1 drops as it comes to room temperature, which means the solubility of the drops. The sample must have been saturated in NaCl , because when the solubility drops some of the precipitates. Since it comes from the same well, we can assume Sample #2 is also saturated in . But the temperature of Sample #2 rises as it comes to room temperature, which will increase the solubility of the salt and allow even more to dissolve. Certainly none of the already dissolved in this sample will precipitate.

A student has two unopened 33cL cans containing carbonated water. Can A has been stored in the garage (32°C) and can B has been stored in the fridge (8°C). The student opens one can at the time, both cans make a fizz.

Predict what will be observed in the experiment.

• Can A will make a louder and stronger fizz than can B.

Can B will make a louder and stronger fizz than can A.

The fizz will be the same for both cans.

There is not enough information to predict which can will make the louder fizz.

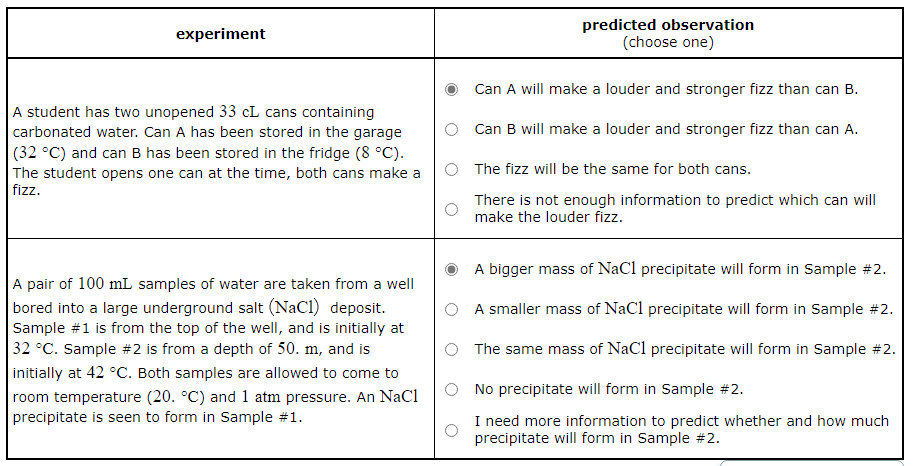
A pair of 100mL samples of water are taken from a well bored into a large underground salt (NaCl) deposit. Sample #1 is from the top of the well, and is initially at 32°C. Sample #2 is from a depth of 50m, and is initially at 42°C. Both samples are allowed to come to room temperature (20°C) and1atmpressure. An NaCl precipitate is seen to form in Sample #1.

Predict what will be observed in the experiment.

	A bigger mass of NaCl precipitate will form in Sample #2.
	A smaller mass of NaCl precipitate will form in Sample #2.
	The same mass of NaCl precipitate will form in Sample #2.
	No precipitate will form in Sample #2.
	I need more information to predict whether and how much precipitate will form in Sample #2.

A chemistry student adds a quantity of an unknown solid compound X to 3.00 L of distilled water at 24° C. After 10 minutes of stirring, all of the X has dissolved. The student then drains off the solution and evaporates the water under vacuum. A precipitate is left behind. The student washes, dries and weighs the precipitate. It weighs 0.75 kg.

1. Using only the information above, can you calculate the solubility of X in water at 24° C?

• Yes

• No

2. If you said yes, calculate it.
   Be sure your answer has a unit symbol and the right number of significant digits.

The solubility of the compound X in water at 24°C cannot be calculated from the given information. Here’s why:

The problem states that a precipitate is left behind after the water is evaporated. This means that the solution was saturated with compound X. However, the mass of the precipitate (0.75 kg) does not necessarily represent the maximum amount of X that could have been dissolved in the 3.00 L of water. It’s possible that less than this amount was originally present, or that more could have been dissolved. Without knowing the exact amount of compound X that was added to the water, we cannot calculate its solubility.

A geochemist in the field takes a 36.0 mL sample of water from a rock pool lined with crystals of a certain mineral compound X. He notes the temperature of the pool, 19° C, and caps the sample carefully. Back in the lab, the geochemist first dilutes the sample with distilled water to 400 mL. Then he filters it and evaporates all the water under vacuum. Crystals of X are left behind. The researcher washes, dries and weighs the crystals. They weigh 1.12 g.

1. Using only the information above, can you calculate the solubility of X in water at 19° C?

• Yes

• No

2. If you said yes, calculate it.
   Be sure your answer has a unit symbol and the right number of significant digits.

Yes, the solubility of the compound X in water at 19°C can be calculated using the given information. The solubility is defined as the maximum amount of solute that can be dissolved in a solvent at a given temperature. Here, the geochemist has dissolved a certain amount of the compound X in water and obtained crystals weighing 1.12 g after evaporating the water.

However, it’s important to note that the original sample was diluted before the evaporation process. Therefore, the 1.12 g of compound X came from the original 36.0 mL of water, not the diluted 400 mL.

So, the solubility of X in water at 19°C would be the mass of the precipitate divided by the volume of water, which is:

{Solubility} = {1.12g} / {36.0mL} = 0.0311 g/mL

This means that 0.0311 g of compound X can be dissolved in 1 mL of water at 19°C. Please note that this is an approximation, and the actual solubility may vary slightly due to factors such as the presence of impurities or measurement errors. Let me know if you need further assistance!

A chemistry student adds a quantity of an unknown solid compound X to 550 mL of distilled water at 21° C. After 10 minutes of stirring, only a little X has dissolved. The student then drains off the solution and evaporates the water under vacuum. A precipitate is left behind. The student washes, dries and weighs the precipitate. It weighs 23.7 g.

1. Using only the information above, can you calculate the solubility of X in water at 21° C?

• Yes

• No

2. If you said yes, calculate it.
   Be sure your answer has a unit symbol and the right number of significant digits.

The solubility of compound X in water at 26°C cannot be calculated from the given information. Here’s why:

The problem states that a certain amount of compound X was dissolved in water and a precipitate weighing 0.15 kg was obtained after evaporating the water. However, we don’t know the initial amount of compound X that was added to the water. Without this information, we cannot determine if the solution was saturated (maximum amount of X was dissolved) or unsaturated (more X could have been dissolved). Therefore, we cannot calculate the solubility of X from this data.

A geochemist in the field takes a small sample of the crystals of mineral compound X from a rock pool lined with more crystals of X. He notes the temperature of the pool, 26° C, and caps the sample carefully. Back in the lab, the geochemist dissolves the crystals in 4.00 L of distilled water. He then filters this solution and evaporates all the water under vacuum. Crystals of X are left behind. The researcher washes, dries and weighs the crystals. They weigh 0.15 kg.

1. Using only the information above, can you calculate the solubility of X in water at 26° C?

• Yes

• No

2. If you said yes, calculate it.
   Be sure your answer has a unit symbol and the right number of significant digits.

At 25.0°C the Henry's Law constant for nitrogen monoxide (NO) gas in water is 0.0019 M/atm.

Calculate the mass in grams of NO gas that can be dissolved in 200mL of water at 25.0°C and a NO partial pressure of 3.99atm.

Be sure your answer has the correct number of significant digits.

0.046 g

---

Sure, here’s the calculation:

1. Calculate the solubility © using Henry’s Law:

   • C = k * P

   • C = 0.0019 M/atm * 3.99 atm

   • C = 0.0076 M

2. Convert the volume of water to liters:

   • V = 200 mL = 0.2 L

3. Find the number of moles of NO that can be dissolved:

   • n = C * V

   • n = 0.0076 M * 0.2 L

   • n = 0.0015 mol

4. Convert moles to grams using the molar mass of NO (30.01 g/mol):

   • m = n * Molar mass

   • m = 0.0015 mol * 30.01 g/mol

   • m = 0.045 g

So, approximately 0.045 g of NO gas can be dissolved in 200 mL of water at 25.0°C and a NO partial pressure of 3.99 atm. Please note that the actual value may vary slightly due to rounding. Let me know if you need further assistance!

At 25.0°C the Henry's Law constant for phosphine (PH3) gas in water is 8.1*10^−3 M/atm.

Calculate the mass in grams of PH3 gas that can be dissolved in 325 mL of water at 25.0°C and a PH3 partial pressure of 0.50 atm.

Be sure your answer has the correct number of significant digits.

0.045 g

---

Sure, here’s the calculation in a simpler format:

1. Calculate the solubility © using Henry’s Law:

   • C = k * P

   • C = 8.1*10^-3 M/atm * 0.50 atm

   • C = 4.05*10^-3 M

2. Convert the volume of water to liters:

   • V = 325 mL = 0.325 L

3. Find the number of moles of PH3 that can be dissolved:

   • n = C * V

   • n = 4.05*10^-3 M * 0.325 L

   • n = 1.316*10^-3 mol

4. Convert moles to grams using the molar mass of PH3 (34.00 g/mol):

   • m = n * Molar mass

   • m = 1.316*10^-3 mol * 34.00 g/mol

   • m = 0.045 g

So, approximately 0.045 g of PH3 gas can be dissolved in 325 mL of water at 25.0°C and a PH3 partial pressure of 0.50 atm. Please note that the actual value may vary slightly due to rounding.

109 mg of an unknown protein are dissolved in enough solvent to make 5.00mL of solution. The osmotic pressure of this solution is measured to be 0.0184atm at 25.0°C.

Calculate the molar mass of the protein. Be sure your answer has the correct number of significant digits.

2.90×10^-4 g/mol

263 mg of an unknown protein are dissolved in enough solvent to make 5.00mL of solution. The osmotic pressure of this solution is measured to be 0.233atm at 25.0°C.

Calculate the molar mass of the protein. Be sure your answer has the correct number of significant digits.

Sure, let’s calculate the number of moles first:

n = \Pi \cdot V / (R \cdot T)

Substituting the given values:

n = 0.233atm \cdot 0.005L / (0.0821 L·atm/K·mol \cdot 298.15K)

After calculating the above expression, we get:

n \approx 4.73 \times 10^{-5} mol

Now, let’s calculate the molar mass of the protein:

M = mass / n

Substituting the given values:

M = 0.263g / 4.73 \times 10^{-5} mol

After calculating the above expression, we get:

M \approx 5560 g/mol

So, the molar mass of the protein is approximately 5560 g/mol. Please note that the final answer is rounded to the correct number of significant digits. Let me know if you need further assistance! 😊

490 mg of an unknown protein are dissolved in enough solvent to make 5.00mL of solution. The osmotic pressure of this solution is measured to be 0.0885atm at 25.0°C.

Calculate the molar mass of the protein. Be sure your answer has the correct number of significant digits.

2.72×10^4

---

Sure, let’s calculate the number of moles first:

n = \Pi \cdot V / (R \cdot T)

Substituting the given values:

n = 0.0885atm \cdot 0.005L / (0.0821 L·atm/K·mol \cdot 298.15K)

After calculating the above expression, we get:

n \approx 1.80 \times 10^{-5} mol

Now, let’s calculate the molar mass of the protein:

M = mass / n

Substituting the given values:

M = 0.490g / 1.80 \times 10^{-5} mol

After calculating the above expression, we get:

M \approx 27200 g/mol

So, the molar mass of the protein is approximately 27200 g/mol. Please note that the final answer is rounded to the correct number of significant digits.

429 mg of an unknown protein are dissolved in enough solvent to make 5.00mL of solution. The osmotic pressure of this solution is measured to be 0.303atm at 25.0°C.

Calculate the molar mass of the protein. Be sure your answer has the correct number of significant digits.

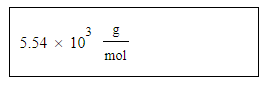
At a certain temperature the vapor pressure of pure acetyl bromide (CH3COBr) is measured to be 0.42atm. Suppose a solution is prepared by mixing 59.8g of acetyl bromide and 66.5g of chloroform (CHCl3).

Calculate the partial pressure of acetyl bromide vapor above this solution. Be sure your answer has the correct number of significant digits.

Note for advanced students: you may assume the solution is ideal.

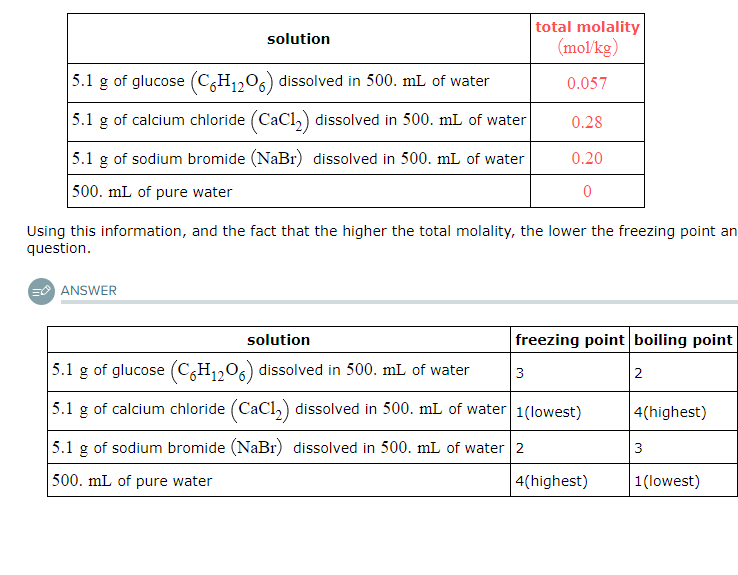
Four liquids are described in the table below. Use the second column of the table to explain the order of their freezing points, and the third column to explain the order of their boiling points.

For example, select '1' in the second column next to the liquid with the lowest freezing point. Select '2' in the second column next to the liquid with the next higher freezing point, and so on. In the third column, select '1' next to the liquid with the lowest boiling point, '2' next to the liquid with the next higher boiling point, and so on.

Note: the density of water is 1.00g/mL.

Sure, let’s calculate the molality for each solution and then determine the order of freezing and boiling points.

The molar masses of the solutes are approximately as follows:

• Glucose (C6H12O6): 180.16 g/mol

• Calcium chloride (CaCl2): 110.98 g/mol

• Sodium bromide (NaBr): 102.89 g/mol

The density of water is approximately 1 g/mL, so 500 mL of water is approximately 500 g or 0.5 kg.

Now, let’s calculate the molality (moles of solute per kg of solvent) for each solution:

1. Glucose solution:

   • Moles of glucose = 5.1 g / 180.16 g/mol = 0.0283 mol

   • Molality = 0.0283 mol / 0.5 kg = 0.0566 mol/kg

2. Calcium chloride solution:

   • Moles of calcium chloride = 5.1 g / 110.98 g/mol = 0.0460 mol

   • Since CaCl2 dissociates into 3 ions in solution, the number of particles is 3 times the number of moles.

   • Molality = 3 * 0.0460 mol / 0.5 kg = 0.276 mol/kg

3. Sodium bromide solution:

   • Moles of sodium bromide = 5.1 g / 102.89 g/mol = 0.0496 mol

   • Since NaBr dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.0496 mol / 0.5 kg = 0.198 mol/kg

4. Pure water:

   • Since there is no solute, the molality is 0.

Now, let’s determine the order of freezing and boiling points. The solution with the highest molality will have the lowest freezing point and the highest boiling point. Conversely, the solution with the lowest molality will have the highest freezing point and the lowest boiling point.

Freezing Point Order (from lowest to highest):

1. Calcium chloride solution

2. Sodium bromide solution

3. Glucose solution

4. Pure water

Boiling Point Order (from lowest to highest):

1. Pure water

2. Glucose solution

3. Sodium bromide solution

4. Calcium chloride solution

I hope this helps! Let me know if you have any other questions.

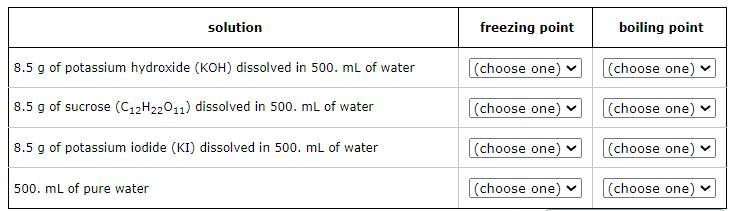
Four liquids are described in the table below. Use the second column of the table to explain the order of their freezing points, and the third column to explain the order of their boiling points.

For example, select '1' in the second column next to the liquid with the lowest freezing point. Select '2' in the second column next to the liquid with the next higher freezing point, and so on. In the third column, select '1' next to the liquid with the lowest boiling point, '2' next to the liquid with the next higher boiling point, and so on.

Note: the density of water is 1.00g/mL.

Sure, let’s calculate the molality for each solution and then determine the order of freezing and boiling points.

The molar masses of the solutes are approximately as follows:

• Potassium hydroxide (KOH): 56.11 g/mol

• Sucrose (C12H22O11): 342.30 g/mol

• Potassium iodide (KI): 166.00 g/mol

The density of water is approximately 1 g/mL, so 500 mL of water is approximately 500 g or 0.5 kg.

Now, let’s calculate the molality (moles of solute per kg of solvent) for each solution:

1. Potassium hydroxide solution:

   • Moles of KOH = 8.5 g / 56.11 g/mol = 0.151 mol

   • Since KOH dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.151 mol / 0.5 kg = 0.604 mol/kg

2. Sucrose solution:

   • Moles of sucrose = 8.5 g / 342.30 g/mol = 0.0248 mol

   • Sucrose does not dissociate in solution, so its molality is not multiplied.

   • Molality = 0.0248 mol / 0.5 kg = 0.0496 mol/kg

3. Potassium iodide solution:

   • Moles of KI = 8.5 g / 166.00 g/mol = 0.0512 mol

   • Since KI dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.0512 mol / 0.5 kg = 0.204 mol/kg

4. Pure water:

   • Since there is no solute, the molality is 0.

Now, let’s determine the order of freezing and boiling points. The solution with the highest molality will have the lowest freezing point and the highest boiling point. Conversely, the solution with the lowest molality will have the highest freezing point and the lowest boiling point.

Freezing Point Order (from lowest to highest):

1. Potassium hydroxide solution

2. Potassium iodide solution

3. Sucrose solution

4. Pure water

Boiling Point Order (from lowest to highest):

1. Pure water

2. Sucrose solution

3. Potassium iodide solution

4. Potassium hydroxide solution

I hope this helps! Let me know if you have any other questions.

Four liquids are described in the table below. Use the second column of the table to explain the order of their freezing points, and the third column to explain the order of their boiling points.

For example, select '1' in the second column next to the liquid with the lowest freezing point. Select '2' in the second column next to the liquid with the next higher freezing point, and so on. In the third column, select '1' next to the liquid with the lowest boiling point, '2' next to the liquid with the next higher boiling point, and so on.

Note: the density of water is 1.00g/mL.

Sure, let’s calculate the molality for each solution and then determine the order of freezing and boiling points.

The molar masses of the solutes are approximately as follows:

• Potassium nitrate (KNO3): 101.10 g/mol

• Hydrobromic acid (HBr): 80.91 g/mol

• Propylene glycol (C3H8O2): 76.10 g/mol

The density of water is approximately 1 g/mL, so 500 mL of water is approximately 500 g or 0.5 kg.

Now, let’s calculate the molality (moles of solute per kg of solvent) for each solution:

1. Potassium nitrate solution:

   • Moles of KNO3 = 8.5 g / 101.10 g/mol = 0.0840 mol

   • Since KNO3 dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.0840 mol / 0.5 kg = 0.336 mol/kg

2. Hydrobromic acid solution:

   • Moles of HBr = 8.5 g / 80.91 g/mol = 0.105 mol

   • Since HBr dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.105 mol / 0.5 kg = 0.420 mol/kg

3. Propylene glycol solution:

   • Moles of propylene glycol = 8.5 g / 76.10 g/mol = 0.112 mol

   • Propylene glycol does not dissociate in solution, so its molality is not multiplied.

   • Molality = 0.112 mol / 0.5 kg = 0.224 mol/kg

4. Pure water:

   • Since there is no solute, the molality is 0.

Now, let’s determine the order of freezing and boiling points. The solution with the highest molality will have the lowest freezing point and the highest boiling point. Conversely, the solution with the lowest molality will have the highest freezing point and the lowest boiling point.

Freezing Point Order (from lowest to highest):

1. Hydrobromic acid solution

2. Potassium nitrate solution

3. Propylene glycol solution

4. Pure water

Boiling Point Order (from lowest to highest):

1. Pure water

2. Propylene glycol solution

3. Potassium nitrate solution

4. Hydrobromic acid solution

Four liquids are described in the table below. Use the second column of the table to explain the order of their freezing points, and the third column to explain the order of their boiling points.

For example, select '1' in the second column next to the liquid with the lowest freezing point. Select '2' in the second column next to the liquid with the next higher freezing point, and so on. In the third column, select '1' next to the liquid with the lowest boiling point, '2' next to the liquid with the next higher boiling point, and so on.

Note: the density of water is 1.00g/mL.

Take into consideration each solution's molality.

Sure, let’s calculate the molality for each solution and then determine the order of freezing and boiling points.

The molar masses of the solutes are approximately as follows:

• Glycerin (C3H8O3): 92.09 g/mol

• Propylene glycol (C3H8O2): 76.10 g/mol

• Potassium hydroxide (KOH): 56.11 g/mol

The density of water is approximately 1 g/mL, so 300 mL of water is approximately 300 g or 0.3 kg.

Now, let’s calculate the molality (moles of solute per kg of solvent) for each solution:

1. Glycerin solution:

   • Moles of glycerin = 7.2 g / 92.09 g/mol = 0.0782 mol

   • Glycerin does not dissociate in solution, so its molality is not multiplied.

   • Molality = 0.0782 mol / 0.3 kg = 0.261 mol/kg

2. Propylene glycol solution:

   • Moles of propylene glycol = 7.2 g / 76.10 g/mol = 0.0946 mol

   • Propylene glycol does not dissociate in solution, so its molality is not multiplied.

   • Molality = 0.0946 mol / 0.3 kg = 0.315 mol/kg

3. Potassium hydroxide solution:

   • Moles of KOH = 7.2 g / 56.11 g/mol = 0.128 mol

   • Since KOH dissociates into 2 ions in solution, the number of particles is 2 times the number of moles.

   • Molality = 2 * 0.128 mol / 0.3 kg = 0.853 mol/kg

4. Pure water:

   • Since there is no solute, the molality is 0.

Now, let’s determine the order of freezing and boiling points. The solution with the highest molality will have the lowest freezing point and the highest boiling point. Conversely, the solution with the lowest molality will have the highest freezing point and the lowest boiling point.

Freezing Point Order (from lowest to highest):

1. Potassium hydroxide solution

2. Propylene glycol solution

3. Glycerin solution

4. Pure water

Boiling Point Order (from lowest to highest):

1. Pure water

2. Glycerin solution

3. Propylene glycol solution

4. Potassium hydroxide solution

I hope this helps! Let me know if you have any other questions.

A small amount of sodium chloride (NaCl) is dissolved in a large amount of water. Imagine separating this process into the four stages sketched below. (These sketches show only a portion of the substances, so you can see the density and distribution of atoms and molecules in them.)

When 258 g of benzamide C7H7NO are dissolved in 1450. g of a certain mystery liquid X, the freezing point of the solution is 8.9 °C lower than the freezing point of pure X. On the other hand, when 258. g of potassium bromide are dissolved in the same mass of X, the freezing point of the solution is 15.6°C lower than the freezing point of pure X.

Calculate the van't Hoff factor for potassium bromide in X. Be sure your answer has a unit symbol, if necessary, and is rounded to the correct number of significant digits.

When 3.81g of a certain molecular compound X are dissolved in 55 g of cyclohexane (C6H12), the freezing point of the solution is measured to be 4.7°C. Calculate the molar mass of X.

Also, be sure your answer has a unit symbol, and is rounded to the correct number of significant digits.