Level Curves and Contour Maps
1/9
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
10 Terms
level curve(s) of a fn
the level curve of a fn f(x,y) of 2 vars are cruves w eqn f(x,y) = k where k is a real number in the RANGE of f(x,y)
contour map
a collection of level curves
tangent plane
a tangent plane approximates a SURFACE at a POINT on the SURFACE/plane (unlike a tangent line which approximates a CURVE at a pt on a CURVE)
formula for tangent plane
derived from the LINEARIZATION of f(x,y) at the point (x0,y0)
this is the tangent plane approximation of f at (x0,y0)
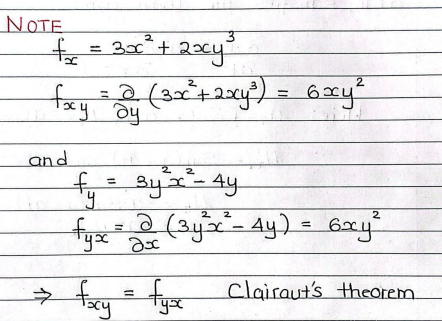
the eqn of the tangent plane to the graph of a fn of two vars at the pt (a,b,f(a,b)) is:
the eqn is known as the LINEAR APPROXIMATION or the TANGENT PLANE APPROXIMATION

differentials

if both fx and fy are continuous, f(x,y) is
differentiable
dz, dy, dx
increment of z (small change in z2 and z1, or delta z), increment of y, increment of x
to calculate dz (increment/slice of z) based on dy and dx
(partial deriv wrt x multiplied by increment of x) + (partial deriv wrt y multiplied by increment of y)
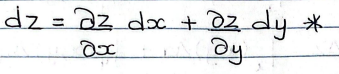
to calculate delta z