Math 150 trig memorization

complementary angle

An angle that, when added to another angle, equals 90 degrees. Complementary angles can be adjacent or separate.

supplementary angle

An angle that, when added to another angle, equals 180 degrees. Supplementary angles can also be adjacent or separate.

co-terminal angle

An angle that shares the same terminal side as another angle but differs by a full rotation of 360 degrees.

degrees to radians

radians = degrees × (π/180).

radians to degrees

degrees = radians × (180/π).

average velocity

v(bar) = displacement/time or r*(theta/t)

omega

w, average change in angle thetaover time, usually measured in radians per second.

angular velocity

v = wr

sin

opp/hyp

cos

adj/hyp

Pythagorean theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides, expressed as a² + b² = c².

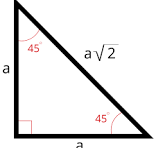
45-45-90 triangle

In a 45-45-90 triangle, the legs are of equal length, and the length of the hypotenuse is equal to the length of a leg multiplied by the square root of 2. 45 degrees = pi/4

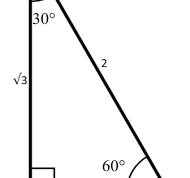
30-60-90 triangle

In a 30-60-90 triangle, the lengths of the sides are in the ratio 1:√3:2. The side opposite the 30-degree angle is the shortest, and the hypotenuse is twice that length. 30 degrees = pi/6, 60 degrees = pi/3 The side opposite the 60-degree angle is 1 times the length of the shortest side.

sin(pi/3)

In trigonometry, sin(pi/3) is equal to √3/2.

cos(pi/3)

In trigonometry, cos(pi/3) is equal to 1/2.

sin(pi/6)

In trigonometry, sin(pi/6) is equal to 1/2.

cos(pi/6)

In trigonometry, cos(pi/6) is equal to √3/2.

cos(0)

In trigonometry, cos(0) is equal to 1.

cos(pi/4)

In trigonometry, cos(pi/4) is equal to √2/2.

cos(pi/2)

In trigonometry, cos(pi/2) is equal to 0.

sin(0)

In trigonometry, sin(0) is equal to 0.

sin(pi/4)

In trigonometry, sin(pi/4) is equal to √2/2.

sin(pi/2)

In trigonometry, sin(pi/2) is equal to 1.

Period of sin

is 2π, meaning it repeats every 2π units along the x-axis.

period of cos

The period of the cosine function is 2π, meaning it repeats every 2π units along the x-axis.

sin domain and range

The domain of the sine function is all real numbers, while its range is from -1 to 1. is an odd function

cos domain and range

The domain of the cosine function is all real numbers, while its range is from -1 to 1. is an even function

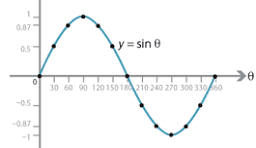
the graph of sin

is a wave that oscillates between -1 and 1, starting at the origin and moving in a smooth manner with a period of 2π.

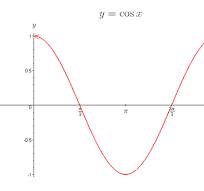
the graph of cos

is a wave-like curve that oscillates between -1 and 1, starting at 1 when x = 0. It is periodic with a period of 2π.

frequency

B

period T

2pi/b

amplitude

IAI

phase shift

bt+c

vertical shift

d

tan

opp/adj

csc

hyp/opp, opposite of sin

sec

hyp/adj, opposite of cos

cot

adj/opp, opposite of tan

sec

1/cos

csc

1/sin

tan

sin/cos

cot

cos/sin

sec(0)

1

sec(pi/6)

2/√3 or 2√3/3

sec(pi/4)

√2

sec(pi/3)

2

sec(pi/2)

undefined

csc(0)

undefined

csc(pi/6)

2

csc(pi/4)

√2.

csc(pi/3)

2√3/3

csc(pi/2)

1

tan(0)

0

tan(pi/6)

1/√3 or √3/3

tan(pi/4)

1

tan(pi/3)

√3

tan(pi/2)

undefined

cot(0)

undefined

cot(pi/6)

√3

cot(pi/4)

1

cot(pi/3)

1/√3 or √3/3

cot(pi/2)

0

graph of sec

is a curve that represents the secant function, showing vertical asymptotes at odd multiples of π/2 where the cosine is zero.

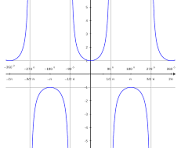
graph of csc

is a curve that represents the cosecant function, showing vertical asymptotes at integer multiples of π where the sine is zero.

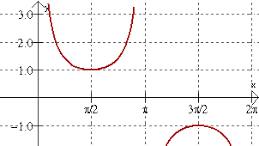
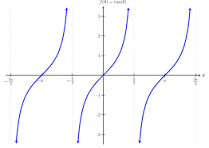
graph of tan

is a curve that represents the tangent function, featuring vertical asymptotes at odd multiples of π/2 where the cosine is zero.

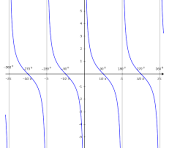
graph of cot

is a curve that represents the cotangent function, exhibiting vertical asymptotes at integer multiples of π where the sine is zero.

sec period

is the length of one complete cycle of the secant function, which is equal to 2π.

csc period

is the length of one complete cycle of the cosecant function, which is equal to 2π.

sec domain and range

The domain of the secant function is all real numbers except where the cosine is zero, specifically at odd multiples of π/2. The range of the secant function is all real numbers less than or equal to -1 or greater than or equal to 1. is even

csc domain and range

The domain of the cosecant function is all real numbers except where the sine is zero, specifically at integer multiples of π. The range of the cosecant function is all real numbers less than or equal to -1 or greater than or equal to 1. is odd

tan domain and range

The domain of the tangent function is all real numbers except where the cosine is zero, specifically at odd multiples of π/2. The range of the tangent function is all real numbers, as it can take any value. is odd

tan period

The period of the tangent function is π, meaning it repeats its values every π units along the x-axis.

cot domain and range

The domain of the cotangent function is all real numbers except where the sine is zero, specifically at integer multiples of π. The range of the cotangent function is all real numbers, similar to tangent. is even

cot period

The period of the cotangent function is π, indicating it repeats its values every π units along the x-axis.