AP-PRECALCULUS EXAM REVIEW

When you plug -x into a polynomial and it ends up identical to the original polynomial, is it even or odd?

even

When you plug -x into a polynomial and it ends up exactly opposite to the original polynomial, is it even or odd?

odd

When you plug -x into a polynomial and it ends up neither identical to the original polynomial or exactly opposite to the original polynomial, is it even or odd?

neither

What does the tangent function look like? (draw it out) What is the period?

The period is pi

What's the domain and range for sin inverse (arcsin)?

Domain: [-1,1] Range: [-pi/2, pi/2]

What's the domain and range for cos inverse (arccos)?

Domain: [-1,1] Range: [0,pi]

What's the domain and range for tan inverse (arctan)?

Domain: (-infinity, infinity) Range: [-pi/2, pi/2]

What's the range for csc?

(-infinity, -1] U [1, infinity)

What does csc look like? (draw it out) Name a few asymptotes.

Asymptotes: 0, pi, 2pi, etc.

What is the range of sec?

(-infinity, -1] U [1, infinity)

What does sec look like? (draw it out) Name a few asymptotes.

Asymptotes: pi/2, 3pi/2, 5pi/2, etc.

What is the range if cot?

(-infinity, infinity)

What does cot look like? (draw it out) Name a few asymptotes.

Asymptotes: -pi, pi, 2pi, etc.

What are the three trig identities?

sin²θ+cos²θ=1

tan²θ+1=sec²θ

cot²θ+1=csc²θ

Angle Sum Identity: sin(α±β) = ?

sinαcosβ±sinβcosα

Angle Sum Identity: cos(α±β) = ?

cosαcosβ∓sinαsinβ

sin2θ = ?

2sinθcosθ

cos2θ = ?

cos²θ-sin²θ

2cos²θ-1

1-2sin²θ

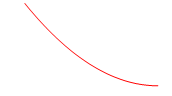
Is this concave up or down? What is happening to the outputs? Is the ROC neg. or pos., increasing or decreasing?

Concave up, outputs are decreasing, ROC is neg. & incr.

Is this concave up or down? What is happening to the outputs? Is the ROC neg. or pos., increasing or decreasing?

Concave up, outputs are increasing, ROC is pos. & incr.

Is this concave up or down? What is happening to the outputs? Is the ROC neg. or pos., increasing or decreasing?

Concave down, outputs are increasing, ROC is pos. & decr.

Is this concave up or down? What is happening to the outputs? Is the ROC neg. or pos., increasing or decreasing?

Concave down, outputs decr., ROC neg. & decr.

cartesian to polar

r²= √x^2+y^2 tan^-1(y/x)

polar to cartesian

x= r*cosθ

y=r*sinθ

rectangular to complex

(a,b) => z= a+b*i

polar (r, θ) to complex

z= r*cosθ + r*sinθ*i

or

z= r(cosθ+i*sinθ)

Formulas for circles

r= acosθ

r=asinθ

(a= diameter)

What kind of symmetry does r=acosθ have?

Polar axis sym

What kind of symmetry does r=asinθ have?

Y-axis sym

Formulas for roses

r = acos(nθ)

r=asin(nθ)

What kind of symmetry does r = acos(nθ) have?

polar axis (x-axis) sym.

What kind of symmetry does r = asin(nθ)

θ = pi/2 sym.

Where is r = acos(nθ) 1st petal?

θ = 0

Where is r = asin(nθ) 1st petal?

θ = pi/2n

If n is odd=? petals

n petals

If n is even=? petals

2n petals

Limacon formulas?

r= a+bcosθ

r= a+bsinθ

If |a|<|b|, what kind of limacon?

loop

If |a| = |b|, what kind of limacon?

cardiod

If |a| > |b|, what kind of limacon?

dimple

What does 2^x look like? (exponential function behaviors)

(0,1) & (1, b)

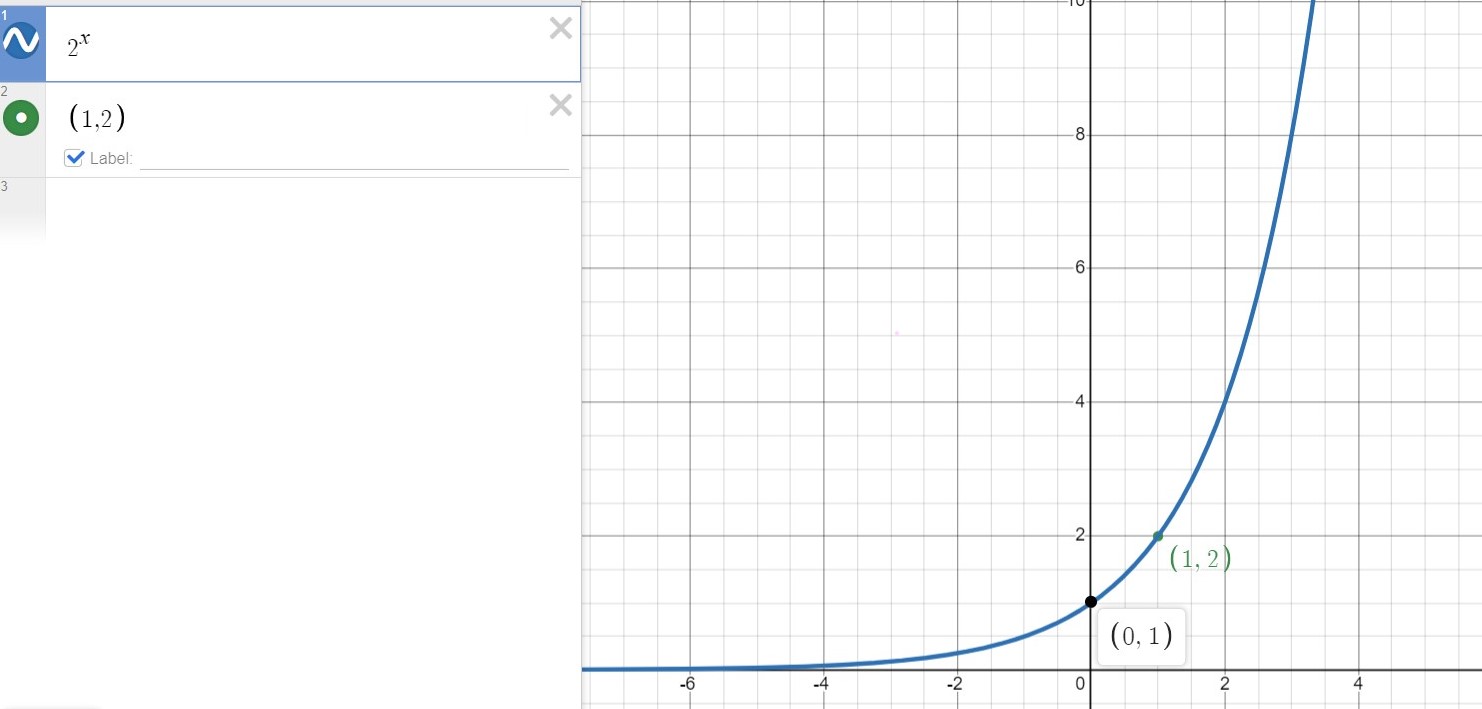
What does ‘k’ stand for in a*b^(x-h) +k (exponential models)

k = horiz. asymptote (not applicable for everything)

Residual = ?

actual-predicted

If the residual value is negative?

overestimate - predicted value too high

If the residual value is positive?

underestimate - predicted value too low

What does log base 2 look like?

(1,0) & (b,1)

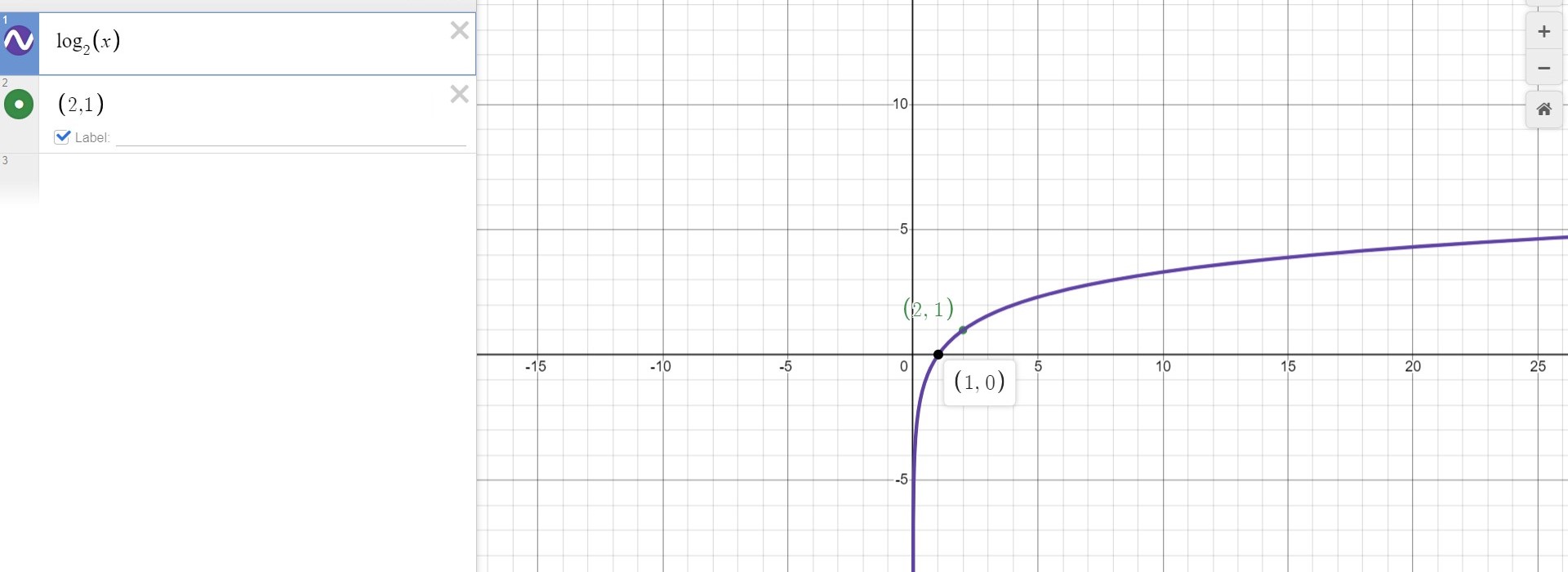
What kind of inputs & outputs do log models have?

proportional inputs, additive outputs

What kind of inputs and outputs do exponential models have?

additive inputs, proportional outputs