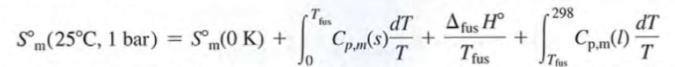Physical Chemistry Exam 1

Operational definition of energy

Energy is the capacity (of a system) to perform work, w

Work is

Force x displacement, amount energy transferred by performing work (kinetic, potential), integral of x1 to x2

force…

causes a body (matter) to accelerate, acceleration is proportional to force (Newton’s 2nd law)

1st law of thermodynamics

energy of the universe is conserved (constant)

Three idealized systems (universe dissected into system and surrounding), distinguished with respect to excheange of energy and matter between system and surroundings

Open: energy and matter are exchanged

Closed: only energy is exchanged

Isolated: no exchange of energy and matter

Sign covention for system

+ work done on system

- work done by system

heat

amount of thermal energy (randomized kinetic and potential energy of atoms and molecules) transfered

Work done on spring with Fex>0 (extension)

Work done on spring (system) positive

Integral

infinite sum of infinitesimally small summands (“limits”) commutative law of addition numbers rules of integration of sums of functions

w units

Nm = kg m²/s² = J (energy)

pressure units

Pa = N/m² = kg/ms²

pressure-volume work of compression

psys vs pex, x positive direction compression, w=(interal)Fexdx = -(integral)pexdV

only determined by external pressure

Irreversible vs reversible expansion

Reversible path can be reversed by an infinitesimal change of the variable that drives the process, implying psys=pex throughout psys = p (expansion stops when pex=p)

Reversible process (path)

process which can be reversed by means of infinitesimal change of a system property without increasing the entropy of the universe, during the entire reversible process the system is in thermodynamic equilibrium with its surroundings

work, w

energy transferred as a result of macroscopic forces, conservative process, pV-work in an electric field

dissipative process: macroscopic forces associated with frictional forces, work transformed into thermal energy

heat, q

energy which transferred as thermal energy (spontaneously from high → low T), defined by temperature change

heat (closed system)

transfer of infinitesimal amount of heat → T increase (dT), ration defines heat capacity (function of T)

C(T):=deltaq/dT → deltaq=C(T)dT

Heat capacities

Molar heat capacity, Cm = C/n (J/K*mol)

Specific heat capacity, c = C/m (J/K*kg)

intensive quantities

molar heat capacity at constant V or p: Cv,m; Cp,m

Cv,m<cp,m b/c pV-expansion work during heating constant p

Closed system first law of thermodynamics

Energy conserved, total energy universe constant, in thermodynamic process energy can be exchanged as q and q between system and surroundings, given a closed system (no exchange of matter) with internal energy U (energy within system) change of U resulting from process: change in U=q+w dU=deltaq+deltaw

(for isolated system change in U=0)

Energy can be transferred to/from system by: work

movement of an object against a force, ie mechanical work/expansion of gases

Energy can be transferred to/from system by: heat

random motion of atoms/molecules, heat transfer occurs when a temperature difference exists

Variables of state (Vos)

describe state of  system, depend only on state and not on path used to reach, can be used to define new VoS: H:=U+pV

Total differential exists for Vos (change in Vos per cycle = 0, dU, dp,…) representing an infinitesimal change of the VoS

Extensive VoS

proprotional to the system mass (V, U, C)

Intensive VoS

indepenent of the system mass (T, p, Cm)

Path variables

q and w are not Vos, infinitesimal amount of q and w denoted as small delta q and w

Classical thermodynamics focuses on…

changes of VoS between states (time required not considered)

states define by values of VoS, final - intial

Energy closed transfer

change in U = U2-U1 <0, any path can be chosen, including reversible

Classification of path

1) Restriction of changes VoS

• isobaric: constant p, change in p=0

• isochoric: constant v, change in v=0

• isothermal: constant T, change in T=0

2) restriction of a path variable

• adiabatic: delta q = 0 (no heat exchange)

3) reversible vs. irreversible

• entropy of universe doesn’t increase with reversible

4) cyclic: initial and final state identical

• all change in VoS=0

Equations of State (EoS) relate VoS

EoS=constraints between VoS, dictate combinations of values set for set of all VoS exist

most frequently used type of EoS, p, V, T

EoS of solids and liquids

Compressibility is low, first approx: V constant, EoS is V(p,T) = V knot improved EoS from linear dependence on T and p → Vm=Vknotm[1+alpha(T-Tknot)][1-ki(p-pknot)]

alpha=coefficient volume expansion

ki=isothermal compressiblity

Eos Ideal gas

no interactions between gas molecules, pV=nRT

EoS ideal gas mixtures

partial pressure pi of component i, pi=niRT/B and p=sumipi, mol fraction xi=ni/sumi(ni) pi=xip

Eos molar heat capacity of monoatomic ideal gas

Cv=3/2R (constant V)

Cp=5/2R (constant p)

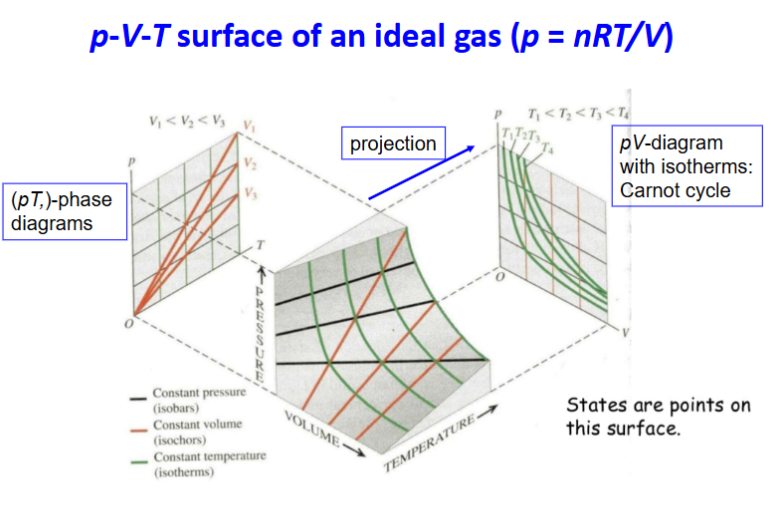
pVT surface ideal gas (diagram)

Equation of state: ‘real gas’

Deviate from ideal because of intermolecular force, volume occupied by gas molecules

Result in empirical VdW equation as approximate EoS: p=(nRT)/(V-nb)-(n²a)/V² → (p+(n²a)/V²)(V-nb)=nRT

a=(parameter model attractive forces between molecules), when a=0, b-(parameter to model volume correction bc intrinsic volume molecules) b=0 (p→0) = EoS ideal gas

new VoS, Enthalpy, H derivation

reversible isobaric process restricted to pV work, change enthalpy=amt reversible heat exchanged with surrounding

H, heat capacities for ideal gas, derivations

H=U+pV=U+nRT —> dH=dpq, rev

result in Cp=Cv+nR

Pure substances → phase transitions → chemical reactions, dependence U and H of pure substance on pVT

EoEoS related VoS p, V, T, for pure substances, compressiblity low:

Heat and cooling liquid water constant at atmospheric pressure, then Cp independent of T, and with molar capacity Cp,m, pV work can be neglected

deltaH approx delta U, Cp approx Cv

Pure substances (gases), pV work for processes with change V, but…

U of an ideal gas depends only on T (not p,V), heat capacities define T dependence U and H

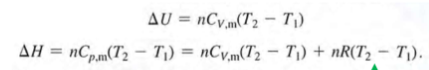
dependence U and H of pure substance

1) Reversible (p=pex) constant pressure expansion work wp, rev → wp=-p(V2-V1)=-nR(T2-T1)

2) Reversible isothermal expansion work

change U = change H = 0 for isotheran processes (pV=nRT=constant)

H=U+nRT for 1st law closed, change U=0 so qt,rev=-wt,rev → all heat transferred to system converted to work

Phase transitions of pure substance

phi, transition a→b: delta(phi)H=Hb-Ha (=qp only if rev pV work wp=-pdeltaphi at constant p

so then deltaphiU=deltaphiH-pdeltaphiV at const p

*HEAT CAPACITY INFINITY DURING PHASE TRANSITION

all latent heat used to drive transition

To obstain deltaphiU and deltaphiH at different T2, cucle constructed given U and H are VoS

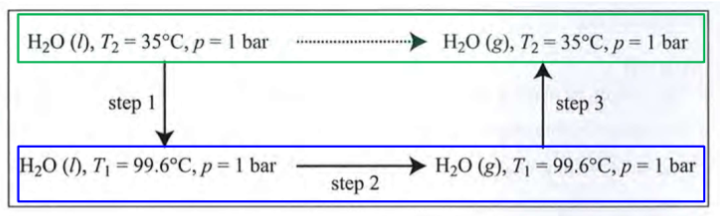
Change of U involving gas, constant p

Difference between U and H due to pV work against constant p

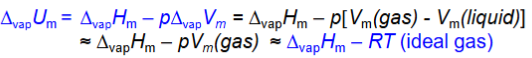
Hm-Hknotm= integral drom Tinitial to T (Cp,m)waterdT

Hm-Hmo=Cp,m(T-To)

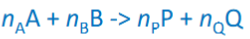
Heat effects chemical reactions

only PV work: deltarU=qv deltarH=qp → deltarH=deltarU+deltar(pV)

deltar(pV)=deltar(nRT)

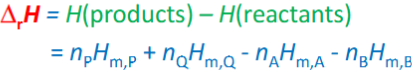
deltarU at constant V,T

deltarU<0, deltarH<0 at constant p, T: exothermic

deltarU>0, deltarH>0 at constant p, T: endothermic

deltarH is VoS, so can be calculated where qp not measured

T dependence deltarH

Known at T1, needed T2,

sum of the equations = overall equations

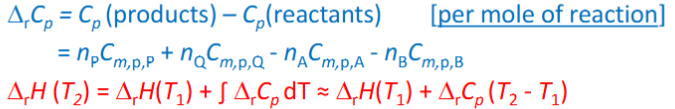
Standard enthalpies of formation Hknot

only differences of enthalpies of rxn of interest

absolute not determined, use molar standrd enthalpes from elements in their most stable allotrope in std state

for elements in most stable Ho=0J/mol

for rxn at 25C: deltarHo=npHop+nqHoq-nAHoA -nBHoB (no enthalpy changes arising from reactant mixing)

Estimation of reaction enthalpu differences from bond dissociation energies, quantum chemical calculations

Entropy

VoS, “S” ds=deltaqrev/T and dS>qirrev/T

change in s = reversible exchange amt of heat/temperature, only reversible path allows to measure, “carnot cycle”

s=(kB)(lnW), absolute values S require stat tehrmodynamics and 3rd law

proportional to logarithm microstates W; kB represents proportionality constant, R=kBNA

Carnot cycle

Idealized/cyclic heat enging, heat to work consisting of 4 reversible steps of ideal gas in closed system without friction

1) Isothermal expansion +q1 → -w1 at Thot

2) Adiabtatic expansion sys cools due to Tcold at -w2

3) Isothermal compression: +w3 → -q3 at Tcold

4) Adiabatic compression sys heats due to Thot at +w4

steps summed to get -wcycle for total amount work in 1 cycle

Discovery of S with the carnot cycle, qrev1/Thot +qrev3/Tcold=0

1) efficiency of Carnot cycle 

as q1/thot + q3/tcold = 0 → q1/thot = -q3/tcold

effiency= 1 - tcold/thot = (thot-tcold)/thot = deltaT/Thot

efficency solely of ratio of temp in heat reservoir

2) carnot cycle can be run in reverse as a heat pump

3) proof by contradiction/indirect proof: coupling carnot heat engine and heat pump with lower efficiency results in construction of “impossible machine” heat flow spontaneously low → high, violates 2nd law

Reversing heat enging → heat pump (wcycle > 0)

COP heat pump: heat or cooling: wcycle>0 COPheat=COPcool+1

Isothermal

Heat exchanged reversibly at constant temperature

cyclic revrsible path: TdS=deltaqrev

pV vs TS diagram: Carnot cycle

deltaU cycle=0, -wcycle,rev=qcycle,rev

deltaqrev=TdS=-pdV → cyclic path integral represents any conceivable reversible cyclic path of closed system

p+V and T+S pairs of conjugate variables

qin,rev exchanged isothermally, deltaS scales with 1/T

deltaShot=qin,rev/Thot<deltaScold=qin,rev/Tcold

2nd Law thermodynamics

entropy system and surroundings = entropy universe = - if isolated, = not ratop if reversible

delta s for expansion ideal gas: reversible vs irrev: 1 mole irreversible against pex=0, no pV work, qirrev=0, but s(surr)=0 and s(sus)>0 (value of s(sys) unknown)

Reversible paths enable measurement of S by…

measuring amount of reversibly exchanged heat, reversiblity implies pex=p throughout expansion

wrev=-RTln(V2/V1)=-RTln2 → qrev=-wrev=RTln2 → s(sys)=qrev/T=Rln2=-s(surr) → suniv=0

s(sys)=integral final-initial delta qrev/T > integral final-initial delta qirrev/T

Reversible process…

process can be reversed by means of infinitesimal change of system property without increasing the entropy of the universe, system in thermodynamic equilibrium with surroundings

given p and T deltarS=?

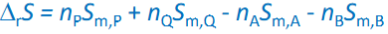
Sm,x

Molar entropy of compound x, reference 1 bar usually 25C

VoS, deltarS not depend on reaction path, cycles can be constructed

absolute entropies can be gotten with 3rd law

3rd law thermodynamics

Entropy pure perfect crystal at 0K=0, only microstate for macrostate of A

S=kBlnW=kVln(1)=0

Temperature dependence S

dS=deltaqrev/T, deltaqrev=CpdT at constant p

dSp/dT=Cp/T

isobaric: constant p = Cpln(T2/T1)

isochoric: constant V = Cvln(T2/T1)

Units S and C: J/K

C always positive → increase T = increase S

Entropy change 1 mol ideal gas heated at constant p

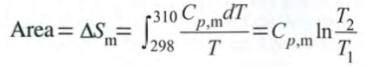
Entropy changes associated with phase transitions

determination of absolute 3rd law entropies

driben reversibly at constant ptrssure associated with deltaphiH=qrev → deltaphiS=deltaphiH/Tphi

Third law entropy Som liquid at 24C, Cp=infinity

For gas: 0→T: solid Tm→Tb: liquid Tb→infinity gas