Physics exam 1

(1/10), Lecture 1(Week 1)
A ball rolls down an incline and off a horizontal ramp. Ignoring air resistance, what force or forces act on the ball as it moves through the air just after leaving the horizontal ramp?
A. The weight of the ball acting vertically down.

B. A horizontal force that maintains the motion.

C. A force whose direction changes as the direction of motion changes.

D. The weight of the ball and a horizontal force.

E. The weight of the ball and a force in the direction of motion.

A. The weight of the ball acting vertically down.

(1/10), Lecture 1(Week 1)
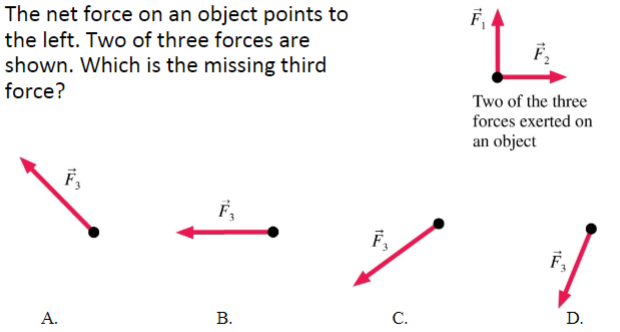
The net force on an object points to the left. Two of three forces are shown. Which is the missing third force?

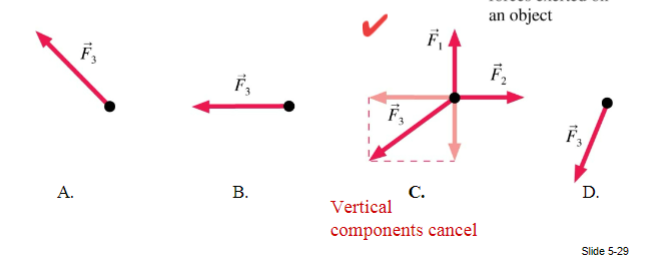
(1/10), Lecture 1(Week 1)
The net force on an object points to the left. Which of the
following descriptions could apply to the object?

A) The object is moving to the left at a constant speed
B) The object is moving to the left with an increasing speed
C) The object is moving to the left with a decreasing speed
D) A, B, and C
E) The object is moving to the right with decreasing speed
F) B and E

F) B and E
Remember, this is all contained in
Newton’s 2nd law as long as you
remember what acceleration means!
Fnet = ma

(1/11), Lecture 1(Week 1), Review
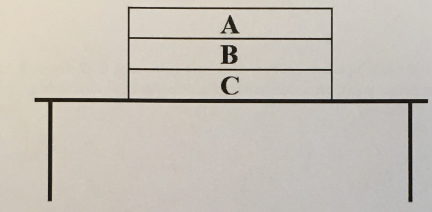
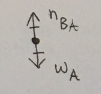
Draw an appropriately labeled free body diagram (FBD) for the book A. Make sure your FBD is consistent with the acceleration of the book

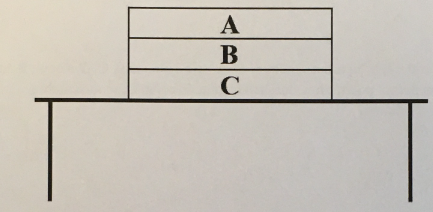
(1/11), Lecture 1(Week 1), Review
Draw an appropriately labeled free body diagram (FBD) for the book B. Make sure your FBD is consistent with the acceleration of the book. Identify any Newton’s 3rd law pairs that are shared between the diagrams. Hint: there should be 3 unique forces on this diagram, it is in contact with two different books!

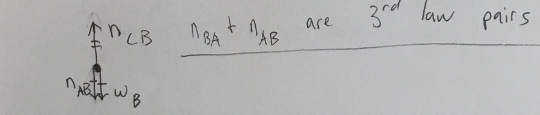
(1/11), Lecture 1(Week 1), Review
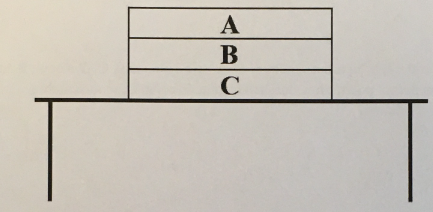
Draw an appropriately labeled free body diagram (FBD) for the book C. Make sure your FBD is consistent with the acceleration of the book. Identify any Newton’s 3rd law pairs that are shared between the diagrams.

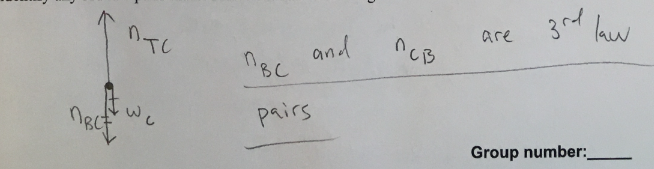
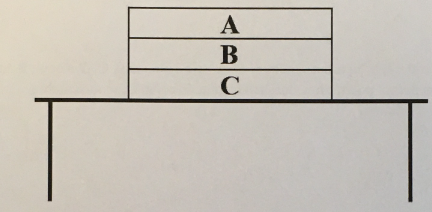
(1/11), Lecture 1(Week 1), Review
Now consider book B again. Hopefully, your FBD includes a normal force from book A and one from books C. Suppose we combine these forces into a single force ( normal). In what direction does this combined force point? How does its magnitude compare to the weight of the force of the book?

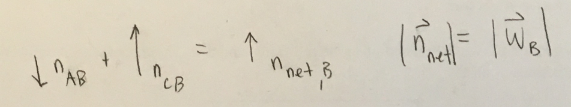
(1/11), Lecture 1(Week 1), Review
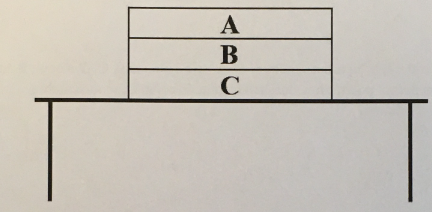
Now lets consider this “combined normal force"‘ acting on book C, due book B and the table. In what direction does it point? How does its magnitude compare to the combined normal force on book B from Q4?

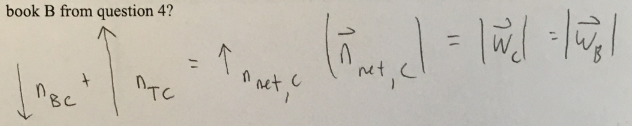
(1/11), Lecture 1(Week 1), Review
Are the individual normal forces actin on book C larger, equal to, or smaller than those acting on book B? Is this consistent with what is happening with the combined normal force as you go down the pile? Why or why not?

The individual forces on book C are larger, but they add up to the same net force because they partially cancel out. In the end, they have to add up to the opposite of teh book’s weight

(1/11), Lecture 1(Week 1), Review
Suppose the stack of books contain 100 identical books instead of 3. How big do you think the combined normal force on the 90th book from the top would be (compare it to the wight of a single book)? How big is the normal force pushing down on it? How much force is pushing up on it?

Nnet would be the same, even though the normal forces would individually be larger. Since there are 89 books on top of it, the normal force pushing down would be 89 times the weight of a single book

(1/12), Lecture 3 (Week 1), CH13
At Earth’s surface, the pressure due to the weight of the air above, often referred to as atmospheric pressure, is about 14.7 pounds per square inch (psi). In SI units, This is about 101,300 Newtons per square meter. Estimate the amount of force the atmosphere exerts on your forearm.

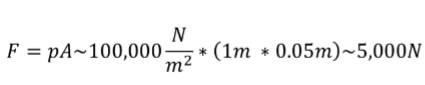
(1/12), Lecture 3 (Week 1), CH13
Fluid, compressible, incompressible

• A fluid is a substance that flows.

• Liquids and gases are fluids.

• Gases are compressible; the volume of a gas is easily increased or decreased.

• Liquids are nearly incompressible; the molecules are packed closely, yet they can move around.

(1/12), Lecture 3 (Week 1), CH13
Density

The mass density is the ratio of mass to volume
p = m/v

SI UNITS FOR SOLIDS: g/cm³

SI UNITS FOR LIQUID: g/ml

CH 13 Q1
If a given power plant released SO2 gas with a volume V of 1200 m³ at a density p of 2.86 kg/m³ at standard pressure and temperature, how many moles n of SO2 are released?

The atomic weight of sulfur is 32.07 u and the atomic weight of oxygen is 16.00 u.

pV = nRT

n = (pV)/(RT)

Data:

p = 1 bar

V = 1200 m³ = 1.2 × 10⁶ dm³

R = 0.083 14 bar·dm³K⁻¹mol⁻¹

T = 273.15 K

Calculation:

n = (1 bar × 1.2 ×10⁶ dm³)/(0.083 14 bar·dm³K⁻¹mol⁻¹ × 273.15 K)

= 52 840 mol

or 5.36×10^4 mol

CH 13 Q2

A 200 mL beaker holds 160 gg of liquid.

What is the liquid's density in SI units?

Given:

• Mass (m) = 160 g

• Volume (V) = 200 mL

1. Convert grams to kilograms: 160 g=0.16 kg (since 1 kg=1000 g).

2. Convert milliliters to cubic meters: 200 mL=0.0002 m³ (since 1 L=0.001 m³).

Now, use the formula for density (ρ):
ρ = m/v
ρ= 0.16kg/0.0002 m³
ρ= 800 kg/m³

(1/12), Lecture 3 (Week 1), CH13
Pressure

Ratio of the force to the area on which the force is exerted
p= F/A

SI UNITS FOR PRESSEURE: N/m²

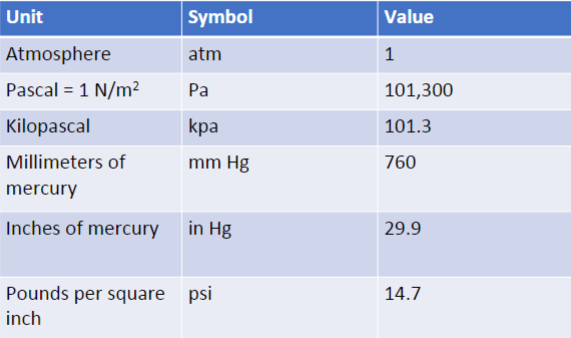
(1/12), Lecture 3 (Week 1), CH13

Pressure in Liquids in Equilibrium

p=p0+ ρgd
Pressure of a liquid with density p at depth d
HYDROSTATIC PRESSURE

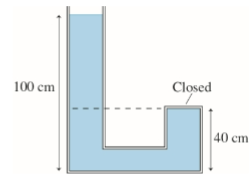
(1/12), Lecture 3 (Week 1), CH13
Water fills the tube shown in the figure. What is the pressure at the top of the closed tube?

(1/12), Lecture 3 (Week 1), CH13
When oil is slowly added to the top of one side of the tube:
(A) The height of the oil will be greater than the height of the water.
(B) The height of the water will be greater than the height of the oil.
(C) The water and oil will be at the same height.

(A) The height of the oil will be greater than the height of the water.

(1/12), Lecture 3 (Week 1), CH13

Hydrostatic Equilibrium

• The pressure is the same at all points on a horizontal line through the liquid.

• The liquid rises to the same height in all open regions of the container.

(1/12), Lecture 3 (Week 1), CH13, In Class #1
Density of cubes. Suppose you have two cubes of identical size (each 5 × 5 × 5 cm), one made of steel and one made of aluminum.

a) Steel has a density of 7,500 kg/m³. What is the mass of the steel block

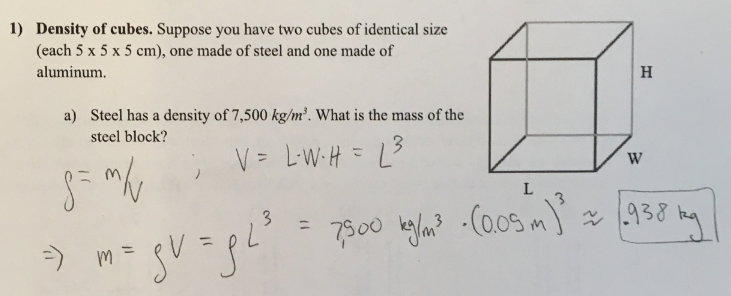
(1/12), Lecture 3 (Week 1), CH13, In Class #1
Density of cubes. Suppose you have two cubes of identical size (each 5 × 5 × 5 cm), one made of steel and one made of aluminum.
b) The aluminum block has a mass of 340 g. Determine its density in SI Units. Does your number make sense. Compare it to that of steel and water.

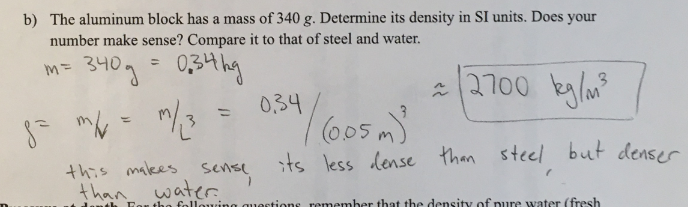
(1/12), Lecture 3 (Week 1), CH13, In Class #1
Pressure at depth. For the following questions, remember that the density of pure water is 1000 kg/m³ and 1atm = 101,300 Pa
a) If you go for a swim in Lake Padden, at what depth would you need to swim to in order for the pressure around you to be equal to 2 atmospheres?

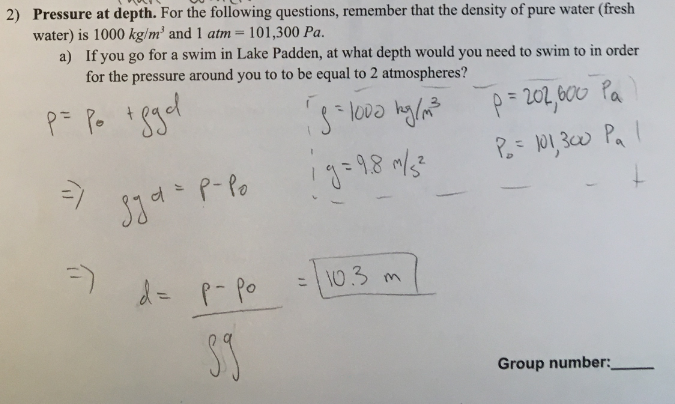
(1/12), Lecture 3 (Week 1), CH13, In Class #1
Pressure at depth. For the following questions, remember that the density of pure water is 1000 kg/m³ and 1atm = 101,300 Pa
b) if you swam to the same depth in bellingham Bay, would the water pressure be greater than, equal to or less that 2 atm. Explain

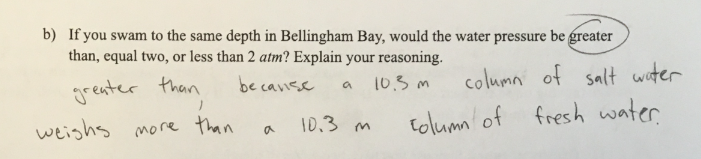
CH13 Q3
The pressure at 10 m below the surface of the ocean is about 2.00×10⁵ Pa.
Part A
Which of the following statements is true?

The weight of a column of seawater 1 m² in cross section and 10 m high is about 2.00×105 N.

The weight of a column of seawater 1 m² in cross section and 10 mm high plus the weight of a column of air with the same cross section extending up to the top of the atmosphere is about 2.00×105 N.

The weight of 1 m³ of seawater at 10 m below the surface of the ocean is about 2.00×105 NN.

The density of seawater is about 2.00×105 times the density of air at sea level.

• The weight of a column of seawater 1 m² in cross section and 10 mm high plus the weight of a column of air with the same cross section extending up to the top of the atmosphere is about 2.00×10⁵ N.

CH13 Q3
The pressure at 10 m below the surface of the ocean is about 2.00×10⁵ Pa.
Part B
Now consider the pressure 20 m below the surface of the ocean. Which of the following statements is true?

The pressure is twice that at a depth of 10 m.

The pressure is the same as that at a depth of 10 m.

The pressure is equal to that at a depth of 10 m plus the weight per 1 m²cross sectional area of a column of seawater 10 m high.

The pressure is equal to the weight per 1 m² cross sectional area of a column of seawater 20 m high.

The pressure is equal to that at a depth of 10 m plus the weight per 1 m²cross sectional area of a column of seawater 10 m high.

(1/19), Lecture 4 (Week 2), CH13
Buoyancy

• the upward force of a liquid.

• The pressure in a liquid increases with depth, so the pressure in a liquid-filled cylinder is greater at the bottom than at the top.

• The pressure exerts a net upward force on a submerged cylinder of:

• FORMULA: Buoyancy: F_b = ρ * V * g

• where F_b is the buoyant force, ρ is the density of the fluid, V is the volume of the displaced fluid, and g is the acceleration due to gravity.

(1/19), Lecture 4 (Week 2), CH13

Archimede’s Principle

• Key concept in fluid mechanics

• States that an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces

• Buoyant force allows objects to float or sink in a fluid

• Formula: Buoyant force = weight of fluid displaced

• Principle used in designing ships, submarines, hot air balloons, and other floating objects

(1/19), Lecture 4 (Week 2), CH13

An object that weighs 4 Newtons floats in a beaker of water. How big is the buoyant force on the object?
A. Less than 4 N
B. Equal to 4 N
C. Greater than 4 N

B. Equal to 4 N

(1/19), Lecture 4 (Week 2), CH13
The same object is placed in a container of alcohol, and it still floats. How big is the buoyant force on the object now?
A. Less than 4 N
B. Equal to 4 N
C. Greater than 4 N

B. Equal to 4 N

(1/19), Lecture 4 (Week 2), CH13

A heavy lead block and a light aluminum block of equal sizes are both submerged in water. Upon which is the buoyant force greater?

A. On the lead block
B. On the aluminum block
C. They both experience the same buoyant force.

C. They both experience the same buoyant force.
Same size → both displace the same volume and weight of water

(1/19), Lecture 4 (Week 2), CH13

Two blocks are of identical size. One is made of lead and sits on the bottom of a pond; the other is of wood and floats on top. Upon which is the buoyant force greater?

A. On the lead block
B. On the wood block
C. They both experience the same buoyant force

A. On the lead block
The fully submerged lead block displaces more much water than wood block

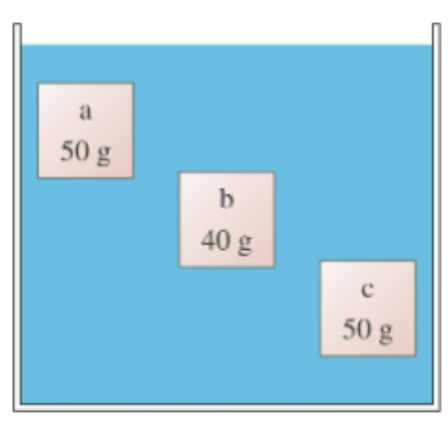
(1/19), Lecture 4 (Week 2), CH13

Blocks a, b, and c are all the same size. Which experiences the largest buoyant force?
A. Block a
B. Block b
C. Block c
D. All have the same buoyant force.
E. Blocks a and c have the same buoyant force, but the buoyant force on block b is different.

D. All have the same buoyant force.

CH13 Q5

Hippos spend much of their lives in water, but amazingly, they don't swim. They have, like manatees, very little body fat. The density of a hippo's body is approximately 1030 kg/m³ so it sinks to the bottom of the freshwater lakes and rivers it frequents--and then it simply walks on the bottom.
Part A

A 1500 kg hippo is completely submerged, standing on the bottom of a lake. What is the approximate value of the upward normal force on the hippo?

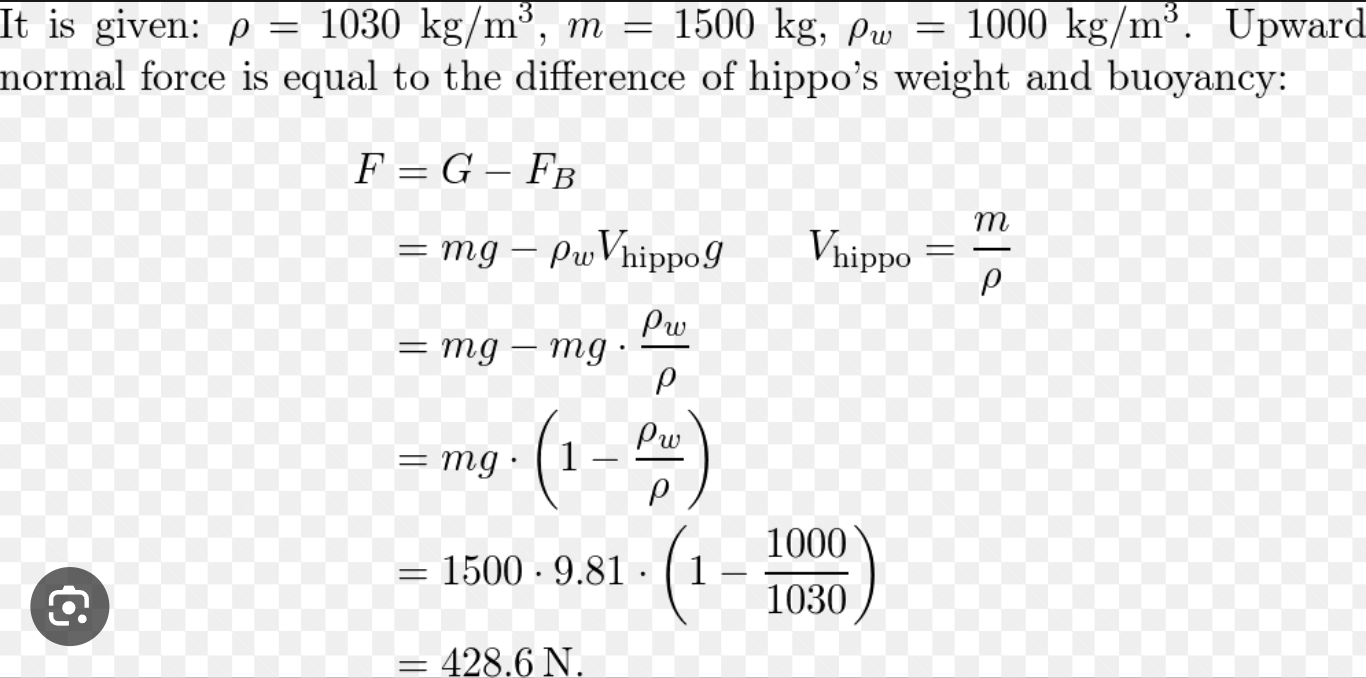
CH13 Q7
An object is placed in a fluid and then released. Assume that the object either floats to the surface (settling so that the object is partly above and partly below the fluid surface) or sinks to the bottom. (Note that for Parts A through D, you should assume that the object has settled in equilibrium.)

• Part A: The magnitude of the buoyant force is equal to the weight of fluid displaced by the object. Under what circumstances is this statement true?

• Part B: The magnitude of the buoyant force is equal to the weight of the amount of fluid that has the same total volume as the object. Under what circumstances is this statement true?

• The magnitude of the buoyant force equals the weight of the object. Under what circumstances is this statement true?

• The magnitude of the buoyant force is less than the weight of the object. Under what circumstances is this statement true?

Part A: for every object submerged partially or completely in a fluid

Part B: for an object completely submerged in a fluid

Part C: for an object that floats

Part D: for an object that sinks

(1/19), Lecture 4 (Week 2), CH13

Fluid in motion

1. The fluid is incompressible, so has constant density.
2. The fluid is non-viscous. We can ignore friction between the fluid and
the walls of the container, and between molecules of the fluid itself.
3. The flow of the fluid is laminar, not turbulent.
• The rising smoke begins as laminar flow, recognizable by the
smooth contours.
• At some point, the smoke undergoes a transition to turbulent
flow.
• A laminar-to-turbulent transition is not uncommon in fluid flow.
• Our model of fluids can only be applied to laminar flow.

(1/19), Lecture 4 (Week 2), CH13
Continuity

• a physical quantity remains unchanged as long as there are no sources or sinks within a given system.

• Conservation of Mass: Continuity equation is used to express the conservation of mass in fluid dynamics, stating that the mass flow rate into a control volume is equal to the mass flow rate out of it.

• Equation: A1v1 = A2v2, where A represents the cross-sectional area and v represents the velocity of the fluid.

CH13 Q8

Your low-flow showerhead is delivering water at 1.3×10^-4 m³a/s about 2.1 gallons per minute.
If this is the only water being used in your house, how fast is the water moving through your house's water supply line, which has a diameter of 0.021 mm (about 3/4 of an inch)?

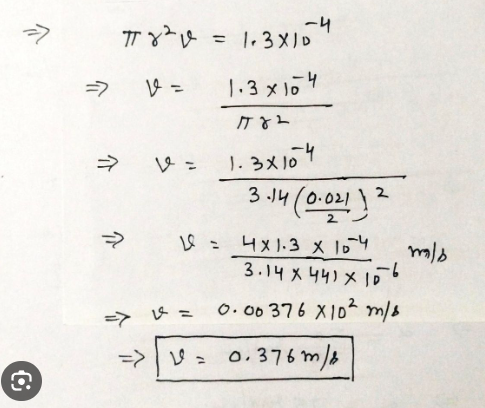
CH13 Q10
When you urinate, you increase pressure in your bladder to produce the flow. For an elephant, gravity does the work. An elephant urinates at a remarkable rate of 0.0060 m³ (a bit over a gallon and a half) per second. Assume that the urine exits 1.0 m below the bladder and passes through the urethra, which we can model as a tube of diameter 8.0 cm and length 1.2 m. Assume that urine has the same density as water, and that viscosity can be ignored for this flow.

Part A: What is the speed of the flow?

Part B: If we assume that the liquid is at rest in the bladder (a reasonable assumption) and that the pressure where the urine exits is equal to atmospheric pressure, what does Bernoulli's equation give for the gauge pressure in the bladder?

1) Let's use the fluid continuity equation

       Q = A v
The area of ​​a circle is

      A = π r2 = π d²

 v = Q / A = Q 4 / pi d²

     v = 0.006 4/π 0.08²

     v =  1.19 m / s

2) write Bernoulli's equation, where point 1 is the bladder and point 2 is the urine exit point

     P₁ + ½ rho v₁² + rho g y₁ = P₂ + ½ rho v₂² + rho g y₂

The exercise tell us

P₂ = 1.0013 105 Pa

v₁ = 0

y₁ = 1 m

y₂=0  

Rho (water) = 1000 kg / m³

P₁ + rho y₁ = P₂ + ½ rho v₂²

      P₁ = P₂ + ½ rho v₂² - rho g y₁

      P₁ = 1.013 10⁵ + ½ 1000 (1.19)² - 1000 9.8 1

      P₁ = 1.013 10⁵ +708.5  - 9800

      P₁ =  92208.5Pa

      P₁ = 0.922 10⁵ Pa

(1/19), Lecture 4 (Week 2), CH13

Bernoulli's Principle

Bernoulli's Principle: Continuity is closely related to Bernoulli's principle, which states that as the velocity of a fluid increases, its pressure decreases, and vice versa.

(1/19), Lecture 4 (Week 2), CH13, In class #2

Suppose that he used a scale to weigh the crown in air, and while completely submerged in water. In air, the scale read 7.5 N, and in water it read 6.8 N

a) determine the mass, in kg, of the crown. Use g= 9.8 m/s²

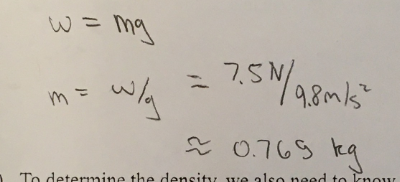
(1/19), Lecture 4 (Week 2), CH13, In class #2
To determine the density, we also need to know the crown’s volume., Draw a FBD for the crown while it is fully submerged and in contact with scale. Consider the buoyant force to be a single force.

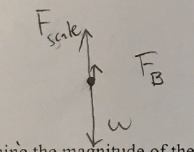
(1/19), Lecture 4 (Week 2), CH13 In class #2
Determine the magnitude of buoyant force on the crown while it was submerged, and determine the crown’s volume using Archimedes’ principle

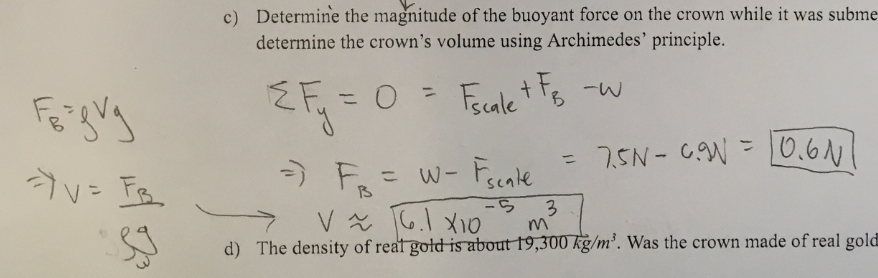
(1/19), Lecture 4 (Week 2), CH13, In class #2

The density of real gold is about 19300 kg/m³. Was the crown made of real gold?

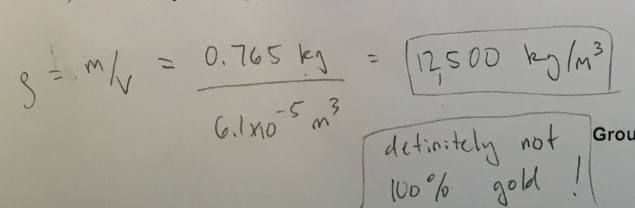
(1/19), Lecture 4 (Week 2), CH13, In class #2

2) A horizontal. fire hose has a nozzle velocity of 40 m/s. The nozzle opening has a radius of 1 cm, while the hose itself has a radius of 4 cm
a) How fast does the water flow through the hose?

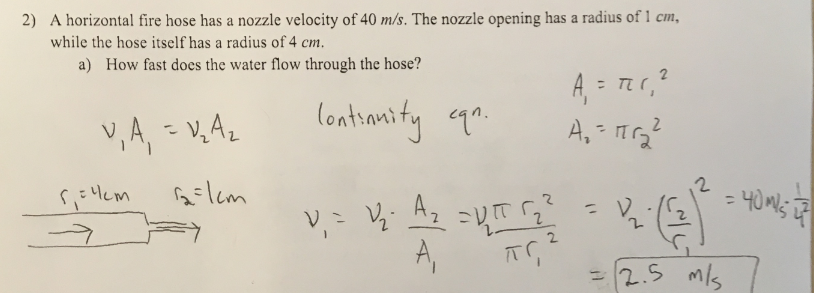
(1/19), Lecture 4 (Week 2), CH13, In class #2

Suppose the hose is hooked up to a fire truck, whose tank a capacity of 750 gallons. Assuming the hose flows at the constant rate mentioned above, how long would it take to empty the entire tank? There are 3.79 liters in a gallon and 1 cubic meter is 1000 liters.

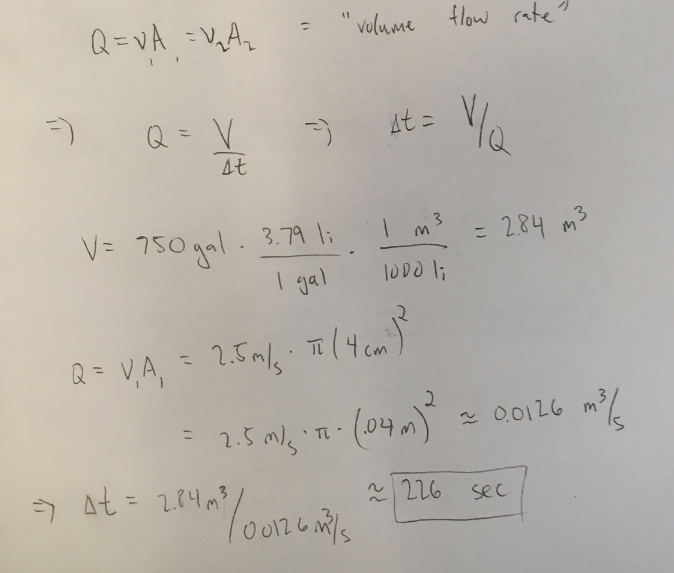
(1/22), Lecture 6 (Week 3), CH11
Efficiency

Process limitations
Fundamental limitation

• The larger the energy losses in a system, the lower its efficiency.

• Reductions in efficiency can arise from two different sources:

• Process limitations cause an energy loss due to practical details. you could design a better, more efficient process.

• Fundamental limitations cause an energy loss due to physical laws that cannot be circumvented

• Equation: n= E out/E in = P out/P in

(1/22), Lecture 6 (Week 3), CH11

A 75 W incandescent bulb and a 15 W fluorescent bulb, as shown in the picture each produce 3.0 W of visible-light energy. What are the efficiencies of these two types of bulbs for converting electric energy into light?

Part B: What if you were using the light for heat? Which light would be more useful for that purpose?

A) Incandescent bulb

B) Fluorescent bulb

Incandescent bulb

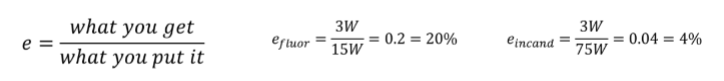
(1/22), Lecture 6 (Week 3), CH11
Units of Energy

• The SI unit of energy is the Joule.

• 1 cal = 4.186 J

• 1 food calorie = 1 Cal = 1000 cal = 1 kcal = 4186 J

(1/22), Lecture 6 (Week 3), CH11
Relating Thermal Energy and Temperature

• Atoms in high-temperature gas move at higher speed than lower-temperature gas.

• The temperature (T) of an object is a measure of the average energy of the atoms
  that make up the object.

• Thermal energy (Eth) is the total energy of the atoms that
  make up the object.

(1/22), Lecture 6 (Week 3), CH11

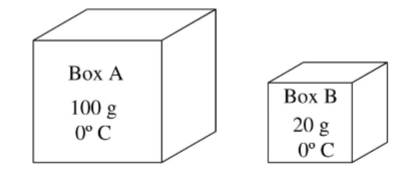
Two containers of the same gas (which we assume to be ideal) have the following masses and temperatures: Which box has the gas with the largest thermal energy?

BOX A

(1/22), Lecture 6 (Week 3), CH11
Temperature scales

• The Celsius scale is defined so that the freezing point of water is 0°C and the boiling point is 100°C.

• The Fahrenheit scale, still widely used in the United States, is
  related to the Celsius scale by:

• T(C) = 5/9 (T(F) - 32)

• T(F) = 9/5 (T(C) +32)

• For the Kelvin scale, zero degrees is the point at which the kinetic
  energy of the atoms is zero.

• Kinetic energy is always positive, so zero on this scale is an absolute zero.

• All temperatures on the Kelvin scale are positive, so it is often called the absolute temperature scale.

• The units are “kelvin” (K).

(1/22), Lecture 6 (Week 3), CH11

Rank the following temperature, T, from smallest to largest

10 K 10 ⁰C 10 ⁰F 283 K
A. 10 K = 10 ⁰C = 10 ⁰F < 283 K
B. 10 K < 10 ⁰F < 10 ⁰C < 283 K
C. 10 K < 10 ⁰F < 10 ⁰C = 283 K
D. 10 ⁰F < 10 K = 10 ⁰C < 283 K

C. 10 K < 10 ⁰F < 10 ⁰C = 283 K

(1/22), Lecture 6 (Week 3), CH11
Rank the following increases in temperatures, ΔT, from smallest largest.
10 K 10 ⁰C 10 ⁰F 283 K
A. 10 K = 10 ⁰C < 10 ⁰F < 283 K
B. 10 K < 10 ⁰F < 10 ⁰C < 283 K
C. 10 K = 10 ⁰C = 10 ⁰F < 283 K
D. 10 ⁰F < 10 K = 10 ⁰C < 283 K

D. 10 ⁰F < 10 K = 10 ⁰C < 283 K

(1/22), Lecture 6 (Week 3), CH11, In class #4
1) Suppose you ride your bike from Boulevard Park (sea- level) up to the top of Sehome Hill (620 feet). Our goal is to estimate how much food we’ve metabolized doing so.

A) let’s make the approximation that we write a constant, low speed. How much mechanical energy did you game? Assume that your bike has a mass of 10 Kg. You can either use your mask in kg if you know it or just guessed that you were a typical human with a mass of around 80 Kg. Use g = 9.8 m/s².

(1/22), Lecture 6 (Week 3), CH11, In class #4

B) let’s also assume that the efficiency of you riding a bicycle is 15%, slightly less than a human body by itself, because you may have to stop a few times at stop signs, and there is some friction and drag. How much energy ( in joules) did you have to metabolize to ride up the hill? How much was lost to heat?

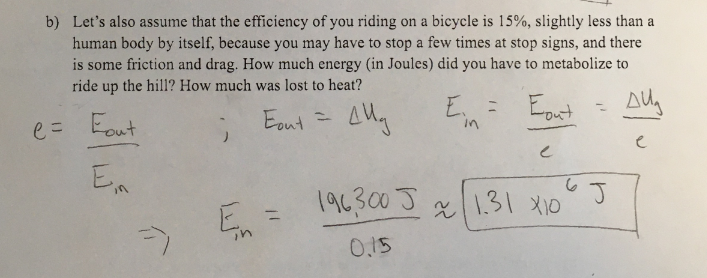
(1/22), Lecture 6 (Week 3), CH11, In class #4

2a) liquid nitrogen is a commonly used cryogen which boils at a temperature of ~77K under 1 atm of pressure. What is the temperature in Celsius? What about Fahrenheit?

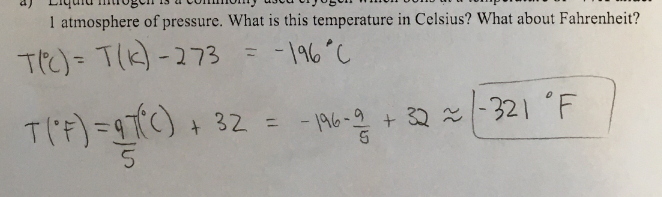
CH11 Q1

The oven draws 1100 WW of power, and you have determined that it heats with an efficiency of 51%. Using this information, determine the time t� it would take to bring 240 mLmL of water from 25∘C∘C to 100∘C∘C . Note that 4.2 JJ of energy is required to raise the temperature of 1.0 mLmL of water by 1.0∘C∘C (the same as for the coffee above).

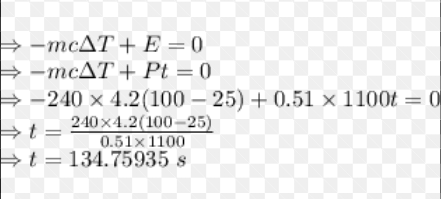
CH11 1. Transforming energy, efficiency and units of energy/power

CH11 HW 1,2,3,4

(1/24), Lecture 7 (Week 3), CH11

Heat

• Thermodynamics is the study of thermal energy and heat and their relationships to other forms of energy and energy transfer.
• Heat is energy transferred between two objects because of a temperature difference between them.
• Heat (Q) always flows readily from the hotter object to the cooler one.

(1/24), Lecture 7 (Week 3), CH11
Atomic Model of heat

• Thermal energy is transferred from the faster moving atoms on the warmer side to the slower moving atoms on the cooler side

Stability: thermal equilibrium

(1/24), Lecture 7 (Week 3), CH11
Thermal Energy

is a property of an object. Thermal Energy is the sum of the microscopic kinetic and
potential energies of the atoms making up an object.

(1/24), Lecture 7 (Week 3), CH11

Heat- Energy that is transferred dur to a temp. dif.
Positive Q

Energy is transferred to the system from the flame
• The thermal energy of the system increases.
• The pot of water is at a lower temperature than the flame

(1/24), Lecture 7 (Week 3), CH11

First Law of Thermodynamics

For systems in which only the thermal energy changes, the change in thermal energy is equal to the energy transferred into or out of the system as work W, heat Q, or both:

Equation

ΔU = Q - W

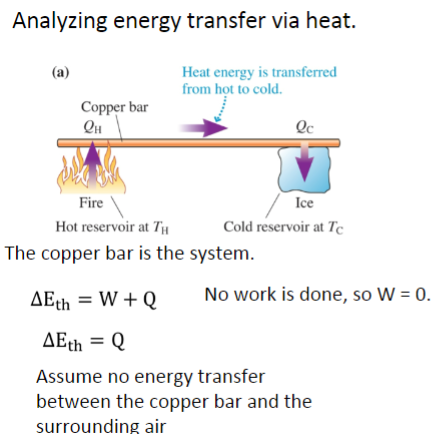
• At the hot end of the bar, 60 joules of energy transfer from the fire to the bar.

• At the cool end of the bar, 40 joules of energy transfer from the bar to the ice.

• By how much does the thermal energy of the bar change?

• What happens to the overall temperature of the bar?

• 20 J

• ΔEth > 0, so T must increase

CH11

100 J is added to a sample of ideal gas as heat. The gas then expands against a piston, doing 70 J of work. During this process
A. The temperature of the gas increases.
B. The temperature of the gas decreases.
C. The temperature of the gas stays the same.

A. The temperature of the gas increases.

• ΔEth= -70J + 100J = +30J

CH11

A steady force pushes in the piston of a well-insulated cylinder. In this process, the temperature of the gas
A. Increases.
B. Stays the same.
C. Decreases.
D. There’s not enough
E. information to tell.

A. Increases.

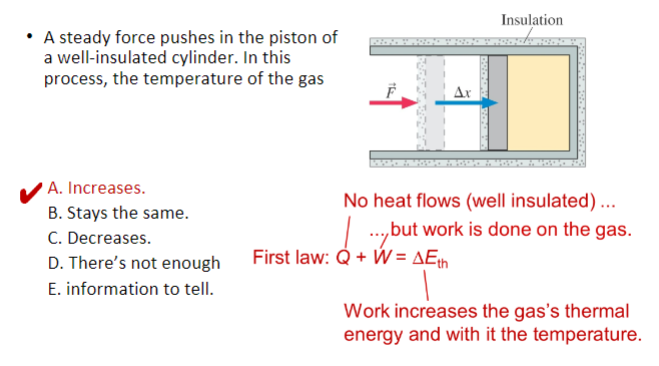
In class activity #5

CH 11, Lecture 8 (week3)

Heat Engines

• No heat engine can operate without exhausting some fraction of the heat into a cold reservoir.

• This isn’t a limitation on our engineering. It’s a fundamental law of nature.

• Wout = Qh - Qc

• n= Wout/Qh = Qh - Qc/Qh

CH 11

Carnot efficiency

nmax = 1- Tc/Th

CH 11

The efficiency of this heat engine is
A. 1.00
B. 0.60
C. 0.50
D. 0.40
E. 0.20

D. 0.40

Spontaneous spreading of thermal energy is irreversible

Iceland has both high geothermal activity, with high temperatures near the surface, and abundant cold surface water. Iceland has many power plants that take advantage of
the proximity of these natural hot and cold reservoirs. One plant uses an underground source at 122°C as the hot reservoir and a nearby lake at 5°C as the cold reservoir. The plant draws 16 MW from the hot reservoir to produce 1.8 MW of electricity. How does the actual efficiency of the plant compare to the theoretical maximum efficiency?

CH 11

Entropy

We use entropy (S) to quantify the spread or dispersal of thermal energy.
• Equilibrium is a state in which thermal energy is maximally dispersed, or shared among all the constituents.
• The entropy of a system is maximum when the system is in equilibrium.
• A good synonym for entropy is disorder

CH 11

Second law of thermodynamics

"The Second Law of Thermodynamics states that the entropy of a closed system always increases over time. It describes the tendency of energy to disperse and become less organized. This law highlights the irreversibility of natural processes and the concept of thermal equilibrium. It helps explain why heat flows from hot to cold objects and why it is impossible to achieve 100% efficiency in energy conversion."

Did the entropy of the system plus environment change in the given
energy transfers: Why?
• A car crashing into a concrete wall (A: Yes B: No)
• Me dropping a bouncy ball on concrete floor (A: Yes B: No)
• Me dropping a book on the floor (A: Yes B: No)
• A cue ball hitting another pool ball (A: Yes B: No)
• Tearing apart a piece of paper (A: Yes B: No)
• Dropping a drop of dye into a cup of water (A: Yes B: No)

• Yes

• No

• Yes

• No

• Yes

• Yes

CH 11

1. Basic thermodynamics:

   1. Temperature: Definition, temperature scales T(K)=T(℃) +( )

      • Slides from lecture 6

      • In class #2

      • Text: 11.3

      • Lab 3

      • Ch. 11 HW #s: 5

   2. 1st law of thermodynamics, thermal energy and heat Eth=Q+( )

      • Slides from lecture 7

      • Group Activity: Heat Engines and 2nd law of Thermo

      • Text: 11.3, 11.4

      • Ch. 11 HW #s: 6, 7, 8

2. Heat engines and 2nd law of thermo =( )QH=( )-( )QH  and max=1-( )TH

   • Slides from lecture 8

   • Group Activity: Heat Engines and 2nd law of Thermo

   • Text: 11.5, 11.7

   • Ch. 11 HW #s: 8, 9, 10, 11

CH 12 Lecture 10 (week4)
Avogadeo’s Number

The number of atoms or molecules in one mole of a substance.

Equation: n= N/N_A

6.022 × 10^23.

Ch12

Global CO2 emissions are estimated to have totaled approximately 36.8 billion metric tons (1 metric ton = 1000 kg) in 2023[1]. How many moles of CO2 is this? How many atoms of carbon?

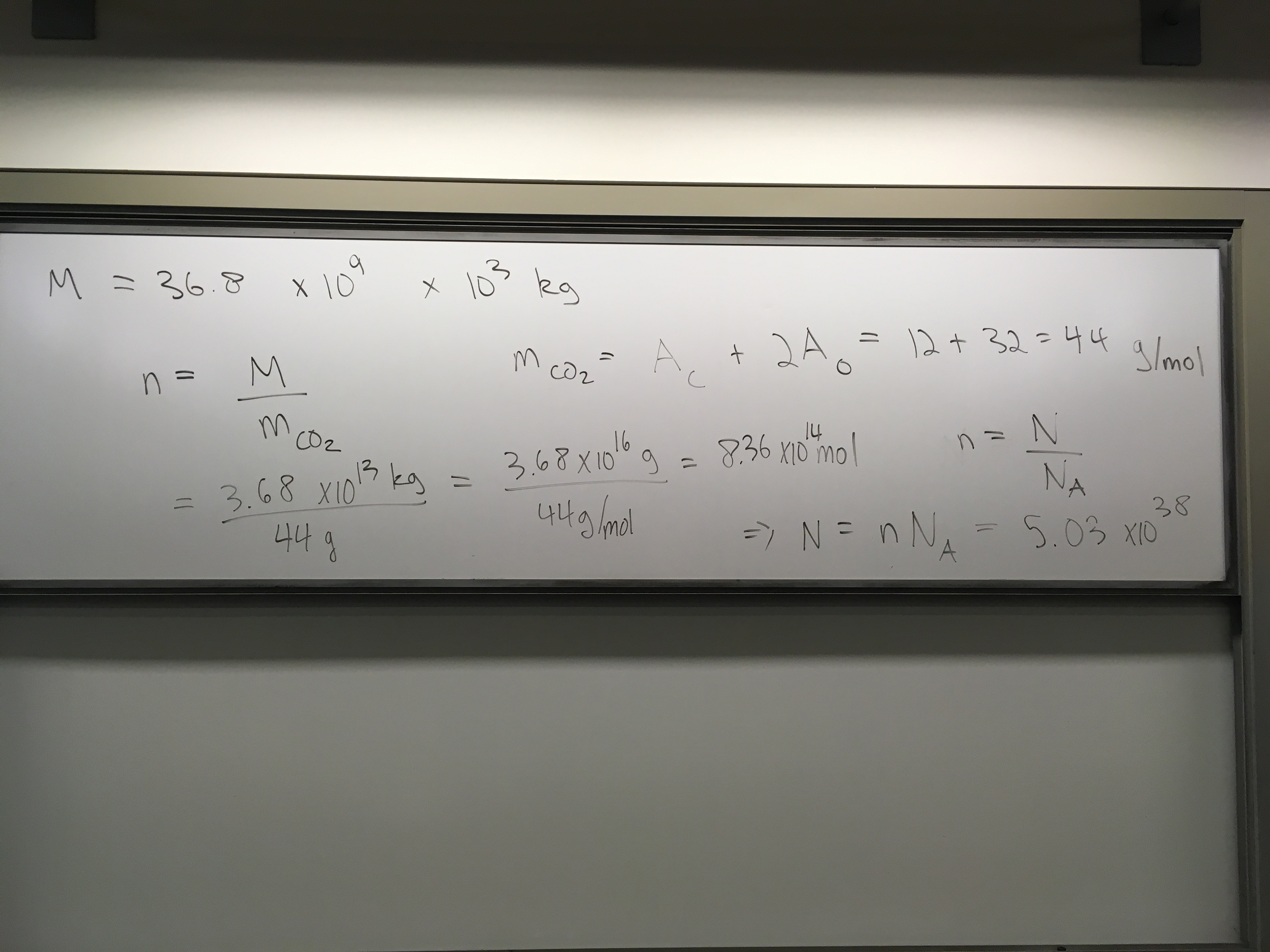
CH12

Atomic model of an ideal gas

The temperature of an ideal gas is directly proportional to the average kinetic energy per atom Kavg:
T= 2/3 K_{avg/ Kb}

_{Kb = 1.38 × 10²3 J/K}

Ch 12

Thermal energy of a monotomic ideal gas

• The thermal energy of an ideal gas containing N atoms is the sum of the kinetic energies of the individual atoms:

• For an ideal gas, thermal energy is directly proportional to temperature. Consequently, a change in the thermal energy of an ideal gas is proportional to a change in temperature:

Equation: E_th = Nk_avg = 3/2 NK_avg T