Precalc Unit 4 Stuff to Know

Relation

Ordered Pairs

Function

A correspondence which assigns every element of set D to one and only one element in Set R

Domain

Values of Input

Range

Values of Output

Zeroes

Roots

Composition of a Function

(F o G)(x)=f(g(x))

Cubic Point of Symmetry value

x=-b/3a

Odd Function

-f(x)=f(-x)

Even Function

f(x)=f(-x)

If a graph is symmetrical to the X axis

Has points (x,y) & (x,-y)

If a graph is symmetrical to the Y axis

Has points (x,y) & (-x,y)

If a graph is symmetrical to y=x

Has points (x,y) & (y,x)

If a graph is symmetrical to the origin

Has points (x,y) & (-x,-y)

Amplitutude of a function

(y_Max-y_min)/2

Period of a function

The range/length over which the pattern repeats

how does function y=f(x), with period P and Amplitude A change with multiplying coefiicient

y=cf(x), has period P & amplitude cA

Y=f(cx) has period P/c & amplitude A

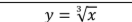
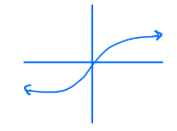
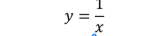
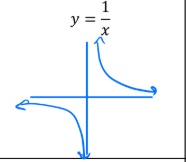
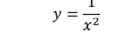
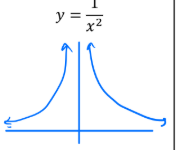
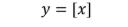
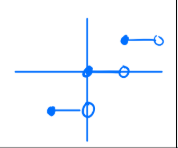
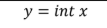
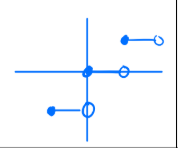
How to tell if a graph is a one to one function

Passes the Vertical AND Horizontal line test

How to verify Analytically if a graph has an inverse

Prove g(g^-1(x))=x and g^-1(g(x))=x

Domain of Composition

Intersection of Inner function & Composition function

Inverse of (F o G)

(F o G)^-1 and (F^-1 o G^-1)