WJEC AS Physics Unit 1.5 - Solids Under Stress

Hooke’s Law

The tension in a spring or wire is proportional to its extension from its natural length, provided the extension is not too great

Equation for Hooke’s Law

F=kx

Where F=Force (N), spring constant (Nm^-1) and x=displacement/extension (m)

How Hooke’s Law can be seen being obeyed on a Force-Extension graph

The line will be straight

Spring constant

The force per unit extension (Nm^-1)

Area under a force-extension graph

• The work done in deforming a solid

• 1/2Fx if Hooke’s law is obeyed

• W=1/2Fx and F=kx may be combined to give W=1/2kx²

Graph of F against x

• y-axis = F

• x-axis = x

• Gradient = k (spring constant)

• Area under graph = Work done in stretching. 1/2Fx if Hooke’s Law obeyed

Tensile stress

• σ

• Stress is the force per unit cross-sectional area when equal opposing forces act on a body.

• Unit; Pa or Nm^-2

• σ = F/A

• When a force is applied to the surfaces of a solid material, it develops a stress

Equation for tensile stress

σ = F/A

Units of tensile stress

Nm^-2 or Pa

Tensile strain

• ε

• Strain is defined as the extension per unit length due to an applied stress.

• Unit: none

• Dimensionless as = m/m. its base units are m * m^-1 which = 1, thus having no units.

• ε = ∆l/l

Equation for tensile strain

• ε = ∆l/l or Extension (x)/Original Length (L)

Units for tensile strain

None. Dimensionless

Young Modulus

• E

• Young modulus, E = tensile stress/tensile strain or E = σ/ε when Hooke’s Law applies

• Unless otherwise indicated this is defined for the Hooke’s law region.

• Unit: Pa or Nm^-2

• Gradient of elastic region of stress-strain graph

Gradient of a stress-strain curve

Young Modulus, E

Work done in deforming a solid

• Equal to the area under a force-extension graph, which is 1/2Fx if Hooke’s law is obeyed

• W=1/2Fx and F=kx may be combined to give W=1/2kx²

Equations for energy stored in a spring

E = ½ Fx  Where E = energy, F = force, x = distance and k = spring constant.

E = ½ kx2 Where E = energy, F = force, x = distance and k = spring constant.

Classification of solids

3 types of solid;

1. Crystalline

2. Amorphous

3. Polymeric

Classification of solids as crystalline

• Solid consisting of a crystal, or of many crystals, usually arranged randomly. The latter is strictly a polycrystalline solid.

• Metals are polycrystalline.

• Regular, repeating pattern

Classification of solids as amorphous

• A truly amorphous solid would have atoms arranged quite randomly. Examples are rare. In practice we

• include solids such as glass or brick or ceramics

• no long range order in the way atoms are arranged, though there may be ordered clusters of atoms.

Classification of solids as polymeric

• A solid which is made up of chain-like molecules.

• Formweed when many monome units are joined together

• e.g.; rubber

Equation for Young Modulus

E=σ/ε

Units of Youngs Modulus

Dimenionless

When Young’s Modulus applies

When Hooke’s Law applies

Grains

• large number of interlocking crystals

• Orientation of crystal planes=random from one grain to the next

• Grain boundaries have a larger component of impurity atoms which are forced out of the grains during crystallisation

Strain hardening

Molecules stretched in one direction and compressed in another

Grain boundaries

The boundaries between crystals (grains) in a polycrystalline material

Polycrystalline solid

• Solid consisting of many crystals arranged randomly

• E.g. metals

Ductile material

• A metals which can be drawn out into a wire

• This implies that plastic strain occurs under enough stress

Elastic strain

Strain that disappears when the stress is removed, that is the specimen returns to its original size and shape

Plastic strain

Strain that decreases only slightly when the stress is removed. In a metal, it arises from the movement of dislocations within the crystal structure

Effects of dislocations

• A combination of grain boundaries and dislocations is responsible for the mechanical properties of polycrystalline metals

• Metals can be strengthened by introducing barriers to dislocation movement, such as foreign atoms, other dislocations, and more grain boundaries

Strengthening of metals

Necking/Ductile Fracture

• The characteristic fracture process in a ductile material

• The fracture of a rod or wire is preceded by local thinning which increases the stress

Elastic limit

• The point at which deformation ceases to be elastic

• For a specimen, it is usually measured by the maximum force, and for a material, by the maximum stress, before the strain ceases to be elastic

Limit of proportionality

The point behind which Hooke’s law is not longer true. Beyond = elastic limit

Yield point

• Just after the elastic limit

• Point at which the material undergoes a large increase in strain for little/no increase in stress

Breaking point

• material continues in the plastic region until it reaches its breaking point

• Point on a stress-strain curve where the material fractures

Stress-strain/force-extension graph for a ductile material/metal

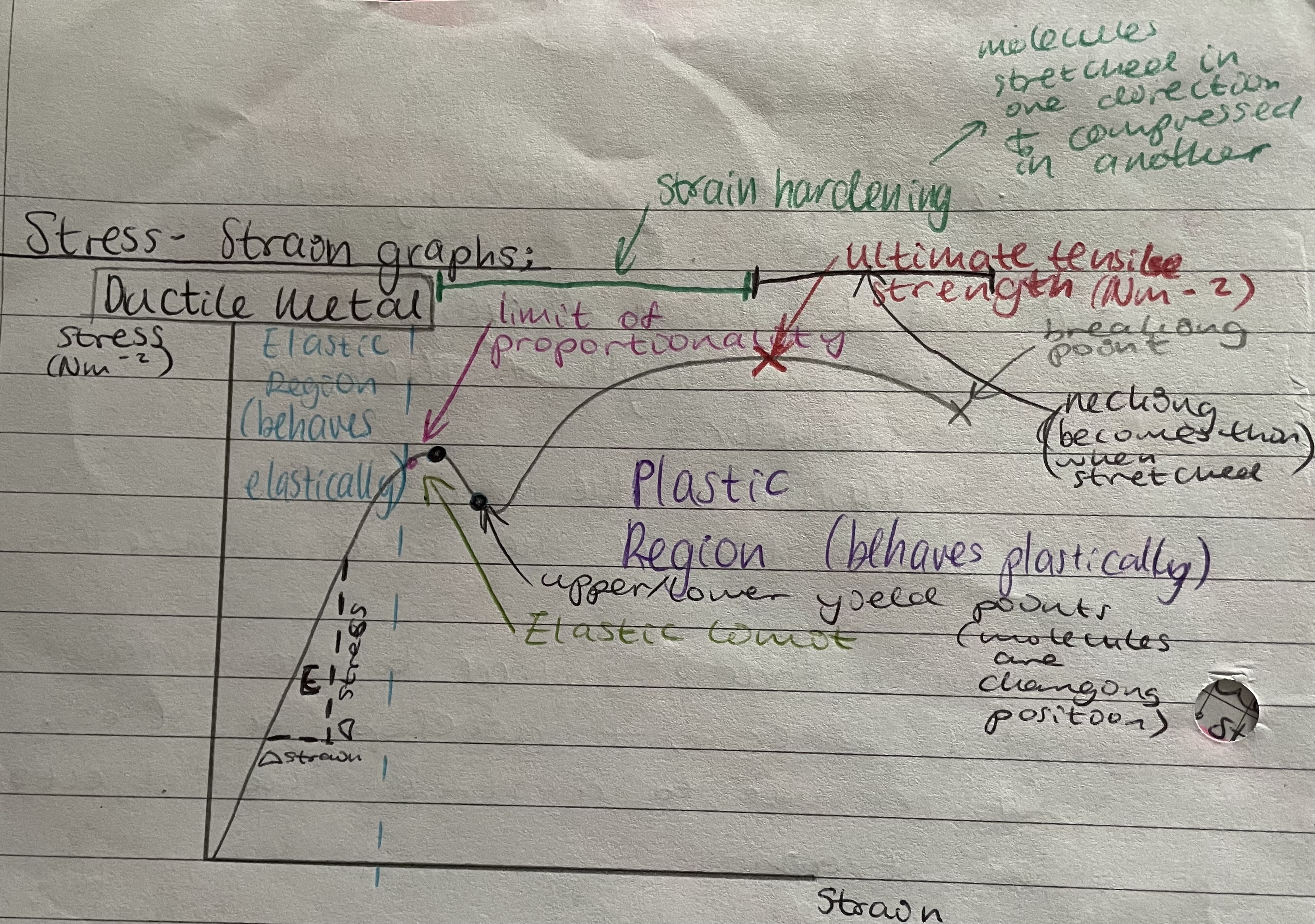
Elastic region of a stress-strain graph for ductile materials

• The region where the material behaves elastically, gradient = young modulus and Hooke’s law is obeyed, undergoes elastic stretching

• Linear portion of the graph before limit of proportionality is reached

Plastic region of a stress-strain graph for ductile materials

• Strain hardening and then necking

• Curve region of graph

Elastic limit of a stress-strain graph for ductile materials

• Point on peak after limit of proportionality at which deformation ceases to be plastic, maximum stress before strain ceases to be elastic

Limit of proportionality of a stress-strain graph for ductile materials

Where liner region/elastic region comes to an end

Yield point of a stress-strain graph for ductile materials

• Point in do just after EL

• MOLECULES ARE CHANGING POSITION

Breaking point of a stress-strain graph for ductile materials

• Point at end of graph at which the material fractures

Ultimate tensile strength

• Nm^-2

• The curve bend downwards behind the UTS

• The maximum stress it can withstand while being stretched or pulled before it breaks

Ultimate tensile strength on a force-extension graph for ductile metal

• Point at which curve begins to bend downwards

Process of elastic deformation/strain

• For a material under low tension, separation between lattice particles is increased

• Forces between the particles pull them back into their initial position when tension is removed

Process of plastic deformation/strain

• Caused by an irreversible rearrangement of particles

• Made possible by edge dislocations

• Individual ions only move slightly

• Ions next to and in edge dislocations drop into a lower PE position in the body plane

• Extra ½ plane moves to right/direction force is acting in until it reaches the grain boundary

• The crystal becomes elongated

• The yield stress occurs at the yield point

• The dislocation does not move back when the stress is removed so the elongation is plastic

What occurs after plastic deformation and factors which may affect this

• edge dislocations; can get entangled, limiting their movement

• Size of grains; larger, greater freedom of movement of the dislocations

• Presence of point dislocations; foreign atoms can inhibit the movement of edge dislocations. A void in the lattice spawns more edge dislocations

• Changing composition can affect this

• Heating/quenching to make a metal more or less ductile

• Cold working makes the metal more stiff and less ductile as causes dislocation entanglement

Irregulaities in the lattice of a ductile material

• Dislocations

• Edge dislocations

• Point defect

• In both types, combination of regular lattice, grain boundaries and dislocations is responsible for the mechanical properties of polycrystalline metals

Dislocations in crystals

• certain faults in crystals which (if there are not too many) reduce the stress needed for plans of atoms to slide

Edge dislocation

The edge of an intrusive, incomplete ½ plane of atoms or ions present

Point defects

A lattice ion is missing or a foreign atom/additional ion is present

Brittle material

Material with no region of plastic flow, which, under tension, fails by brittle fracture

Stress-strain graph of a brittle materials

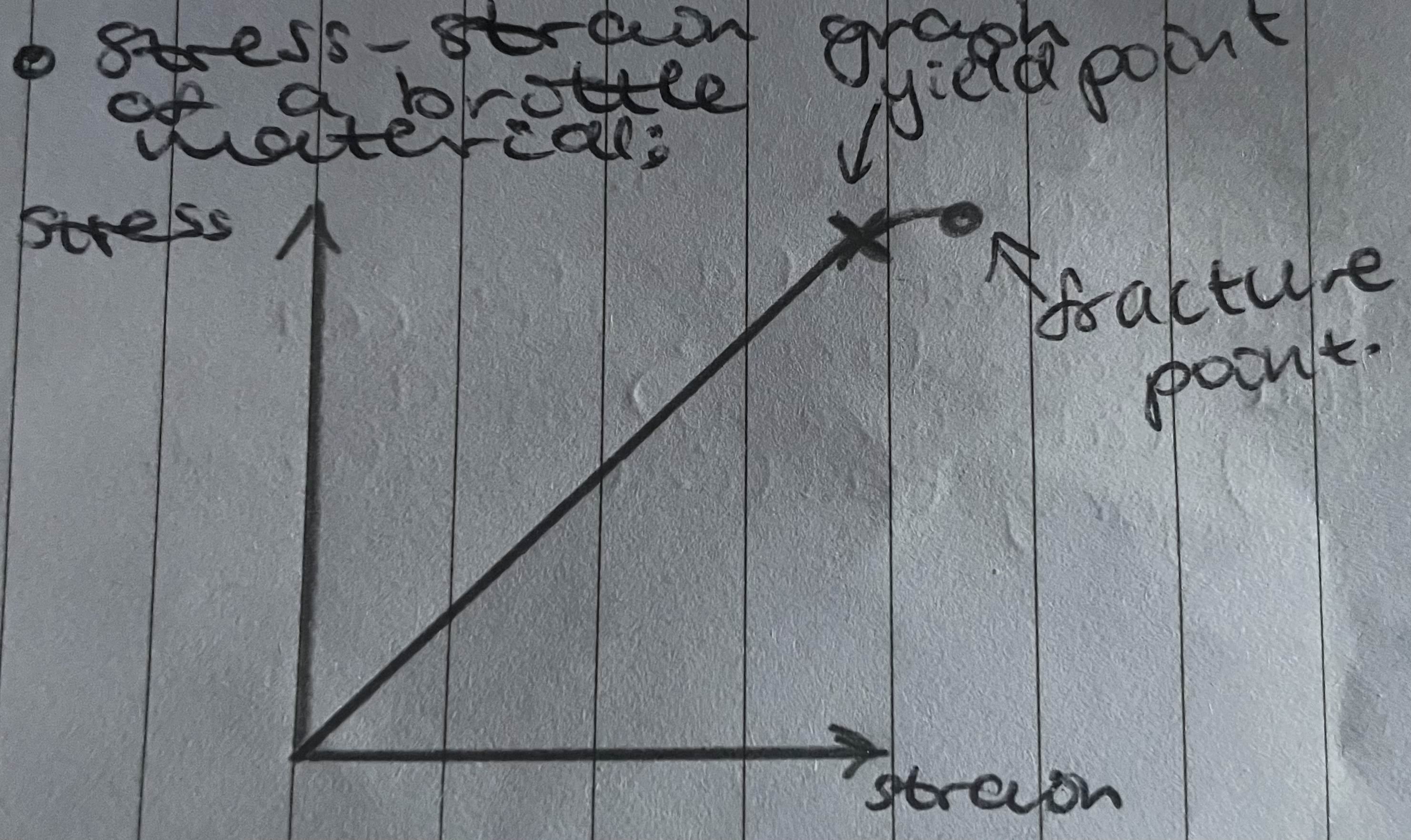
Elastic strain in a brittle material

• Elastic strain occurs and Hooke’s law is obeyed up to fracture

• Small elastic region before fracturing due to high Young Modulus

Brittle fracture

Fracture under tenting of brittle materials by means of crack propagation

Crack propagstion

• Brittle materials undergo brittle fracture by crack propagation

• Weakened by presence of minute cracks in its surface which break bonds

• Stress at tip of cracks = concentrated and bonds break prematurely in the region, allowing the crack to move further through the specimen

• Overloads the next bonds lower down at top of crack and process repeats itself rapidly until glass breaks

Effect of surface imperfections on breaking stress

Reduce breaking stress of a material as it will allow for cracks to develop in thin fibres

Effect of compression on breaking stress

• Breaking stress can be increased by putting the surface under compression

• A much larger stress is required to separate the two sides of the crack and to get the rest of the material into tension so it can separate

Force-extension graph for rubber

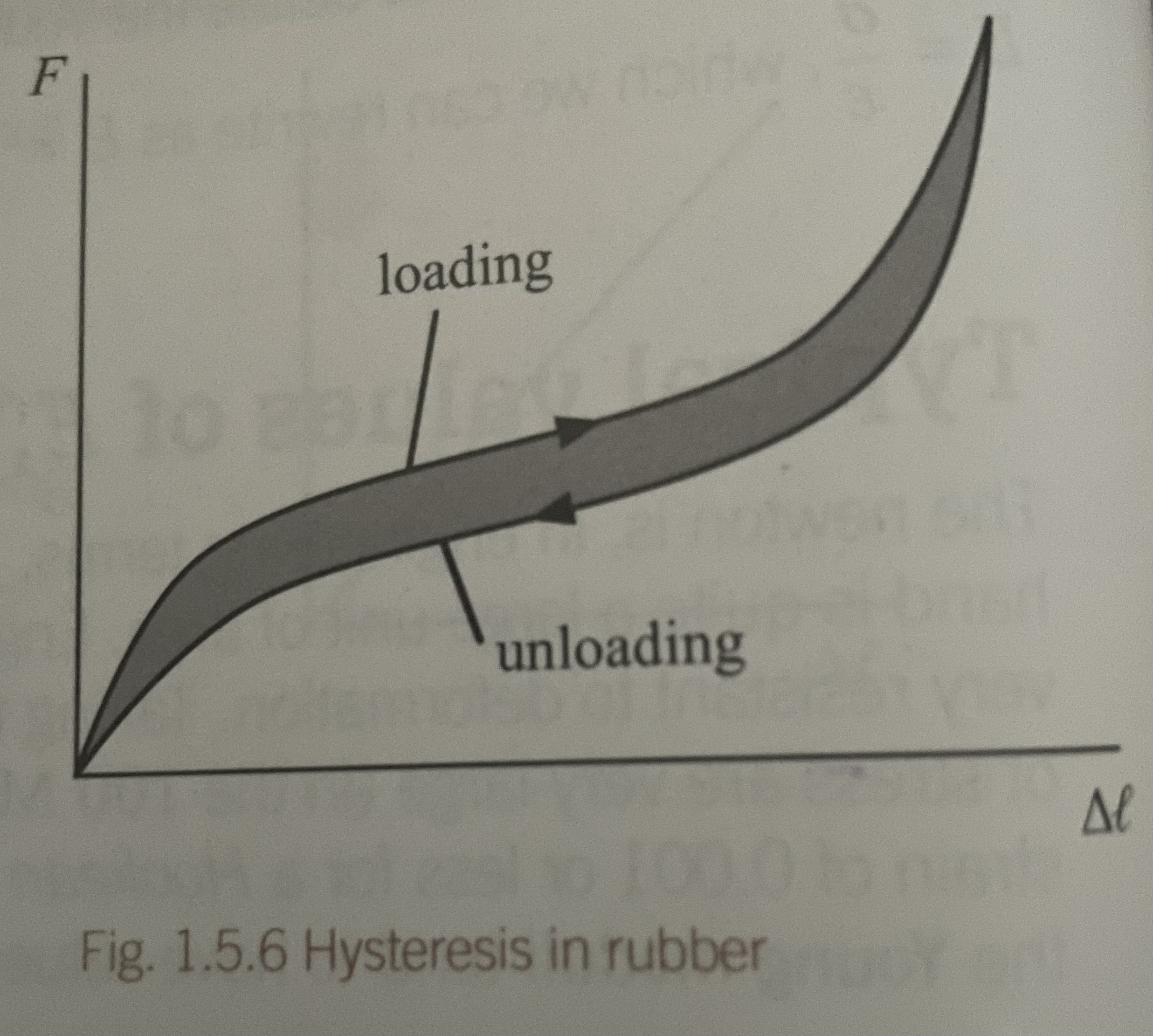
Chacreristsics of a stress-strain graph for rubber

• Hooke’s law only approximately obeyed

• Low Young modulus

• Extension due to straightening of chain molecules against thermal opposition

• Non-linear

• Loading + unloading curves differ - elastic hysterisis

• Exhibits large strain

• Low stress

• Volume stays roughly constant despite large extension

Area under a stress-strain graph for rubber

Energy lost as heat during 1 stretching/relaxing cycle. Shows elastic hysterisis effect

Young modulus of rubber

• Non-linearity of graph means YM can either refer to;

  • gradient of tangent at origin

  • Value of stress/strain for a particular stress

Elastic hysterisis

When a material such as rubber is put under stress and the stress is then relaxed, the stress-strain graphs for increasing and decreasing stress do not coincide, but form a loop. This is hysterisis. Energy lost during stretching cycle for rubber

Permanent set

Load removed, permanent extension which may creep back to zero

Process of stress and strain on rubber

• Start; Chain molecules are being uncoiled and no direct stress is applied to any bonds. High strain, low E, low increase in stress

• End; long chain molecules have been straightened out and direct stress is being applied to the strong covalent C-C bonds along the backbone of the polymer. Very little strain achieved, line is steep and high E

Factors effecting the amount of extension

• Original length of the wire

• Diameter

• Tension in the wire

• The material the wire is made from

Rubber

• can stretch to several time original L

• Force required is much less than other types of materials, e.g. amorphous as bonds not stretched, just rotated

• Presence of cross-linkages of entanglement between/of molecules limits total extension possible

• The thermal motions of the atoms in the molecules, provide the opposition to the extension

• T removed, random molecular motions of atoms re-randomised the shape of the molecules leads to contracting

• Some energy is converted in KE by collisions. Therefore not as much work is done in contracting —> hysterisis effect

Examples of a ductile material

Metals such as copper

Examples of a brittle material

Glass/ceramics