L9: Game Theory II

Sequential game

• Players take turns in making choices

• Previous choices are known to players - still compete information!

• Game represented as a tree (also called extensive form)

Decision tree/extensive form

• Each non-leaf node represents a decision point for some player

  • Non-terminal note: not an endpoint

  • Terminal node: indicates the game is over

• Branches represents available choices/actions

• We can change simultaneous games into sequential games

Utilities are known to both players —> means games are very strategic

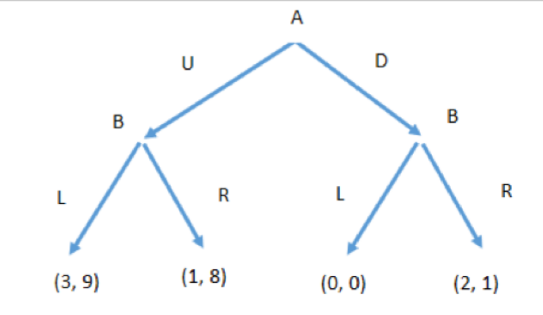
Extensive form example

• Player A goes first, player B reacts to A

• Both Nash equilibria (3, 9) and (2, l) are still there

• What does player A play?

  • You compare the best options on both sides of tree

    • Aka (3,9) and (2,1)

• Which one is now likely to occur?

  • If A plays U: what would B do? L9>8

  • If A plays D: what would B do? R 1 > 0

• What is the equilibrium?

  • (U,L) is Nash equilibrium - only one in sequential games

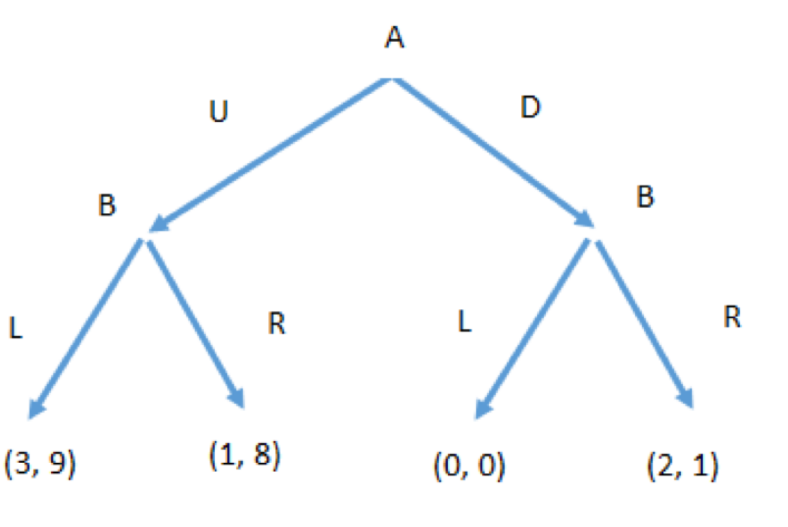
Subgame Perfect Equilibria

• Not all Nash equilibria are sensible in extensive form games

• Players maximize their rewards based off what they can still obtain, not what they could have obtained

• Subgame perfect equilibrium refines the concept of nash equilibrium accordingly

  • Sub game: if we make the equilibrium, we have to make sure is credible (it is reasonable)

    • Need to chip tree down in different games

  • Perfect: by looking at the sub game, we ensure that the threat is credible

  • Equilibrium: no one has the incentive to change their moves

• So, in sequential games we try to rule out threats which are not credible

How to find the subgame perfect equilibria

• Chopping down the tree in different subgames

• A profile of strategies in an extensive form game is a Subgame Perfect Nash equilibrium (SPNE) if it induces a Nash equilibrium in every subgame

  • Start with smaller circles and go bigger —> each little branch, then what is the best between the little branch, then what is the best for the whole tree

Escalation game background

• Two states thinking about going to war with each other or not...

  • State I: accept the status quo or threatens

  • State 2: can responded concede or escalate the conflict

  • State I: can give up or go to war

• To find equilibria: start at the end and move backwards

  • Backward induction

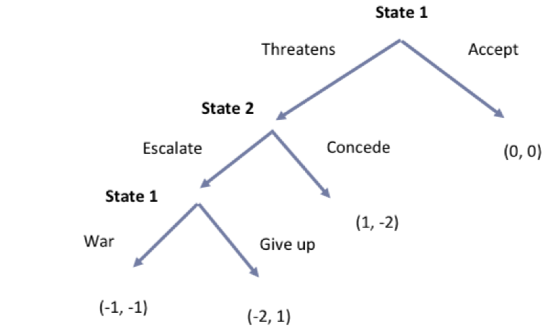
Escalation game equilibria

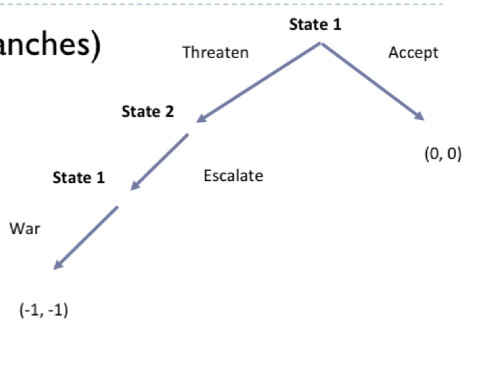
• Back to the initial tree (minus some branches)

• We know:

  • State I prefers war over give up

  • State 2 prefers to escalate over concede

• All redundant branches are no longer in the picture

  • (-1, -1)

• What is the best plan of action for State 1? Why?

  • State 1 → Accept: 0 > -1

• What is the Subgame Perfect Equilibrium (SPE)?

  • (war accept, escalate) OR (war, accept)

    • War, accept notice of state 1 and (escalate) is choice of state 2

    • State 1 chooses to accept only bc they know that otherwise they know they will end up in war 

*SPE Looks at the path to Nash equilibrium and what happens after

Subgame perfect equilibria: details

• A subgame perfect equilibrium is a complete (!) and contingent plan of action

  • It must state what happens on and off the equilibrium path of the game

  • Just mentioning accept, does not tell us WHY state 1 accepts

  • It is only rational in connection to the moves and actions of the other state

    • Especially if you have this weird branch (longer than the other)

• It is important to note that all subgame perfect equilibria are Nash equilibria

  • Since backward induction ensures that each player will play his or her best option at each node, the resulting strategies will correspond to a Nash equilibrium

• In other words:A profile of strategies in an extensive form game is a Subgame Perfect Nash Equilibrium (SPNE) if it induces a Nash equilibrium in every subgame

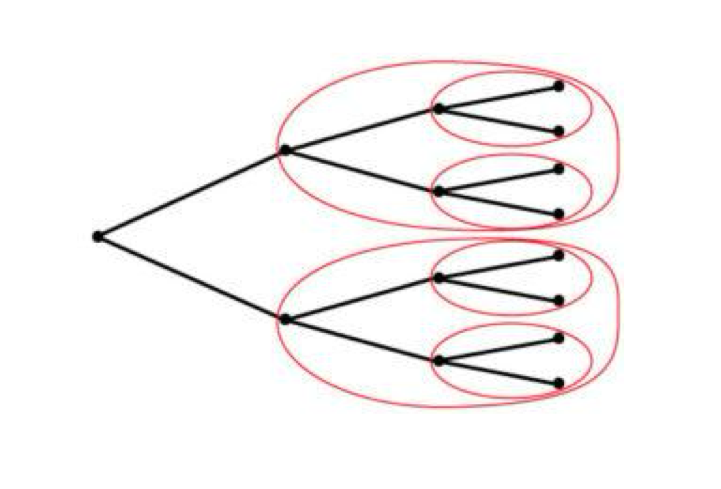
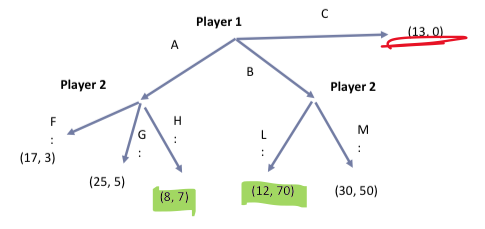
Example: weird branch

C = weird branch —> think omg something happens (threat)

• Green = NE of each sub game

• Red = SPE

SPE = (C, H L)

• Player 1 only play C in light of threat of H and L

Mixed strategy Nash equilibria

exists in a strategic game, when the player does not choose one definite action, but rather, chooses according to a probability distribution over his actions

Pure vs mixed strategies

Pure = assigned 100% probability to only plan

Mixed = assigns probability to a particular action

Matching pennies example

• Story:

  • You and your friend simultaneously reveal a penny

  • If both pennies show heads or both show tails, your friend must pay you
    $1

  • If one penny shows head and the other shows tail, you must pay your friend $1

• What is the PSNE? There isn’t one

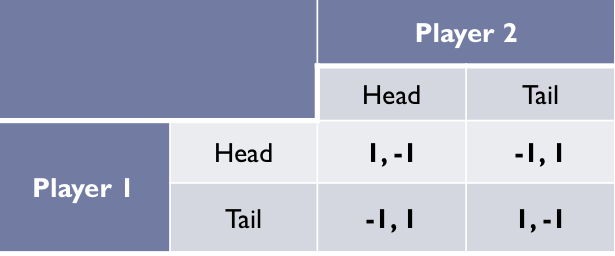
Matching pennies solution

• The matching pennies game is a zero-sum game

• No clear PSNE; there is always an incentives to change...

• John Nash again contributed to the solution of these games:

• If the game is finite (finite number of players and finite number of strategies) and there are no Pure Strategy Nash equilibrium, then there must be a Mixed Strategy Nash Equilibrium

• It is possible to find a randomized mutual strategies that satisfy Nash Equilibrium requirements

Mixed strategies

• a probability distribution over two or more pure strategies

  • If mixtures are mutual best response, the set of strategies is a mixed strategy Nash equilibrium 

  • Assigns probability distribution over pure strategies

  • It is related to expected utility theory and lotteries

• In MSNE, each player's probability distribution makes all other player's indifferent between their pure strategies (only true for 2 x 2 games)

  • Finding point where other player is indifferent to switching

• That is, the utility of playing strategy I must equal the utility of playing strategy 2

Mixed strategy critique

• Randomization, central in mixed strategies, lacks behavioural support: seldom do people make their choices following a lottery

How to calculate Mixed Strategy Nash Equilibrium (MSNE)

1. Find the probability of each outcome to occur in equilibrium

2. For each outcome, multiply the probability by a particular players payoff

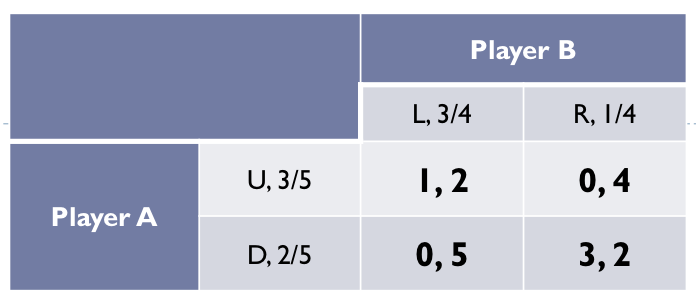
Example mixed strategy

• Two players {A,B}

• 4 actions: Up, Down, Left and Right

• Are there any PSNE? No

• Are there any MSNE?

  • If there is no PSNE there is for SURE a MSNE

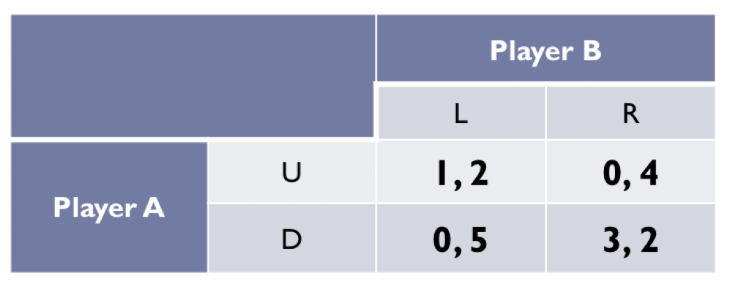
Step 0: player A

• Instead of playing U or D, Player A selects a probability distribution (πu, l- πu), meaning that with a probability (πu) player A will play Up and with a probability (I - πu) will play Down

  • π = p (probability)

• Player A is mixing over the pure strategies Up and Down

• The probability distribution (πu, I- πu) is a mixed strategy for player A

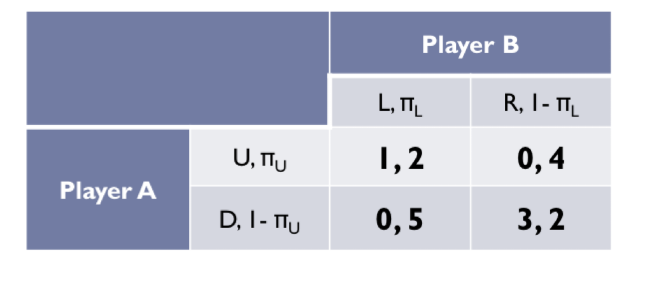
Step 0: player B

• instead of playing L or R, Player B selects a probability distribution (πL, 1 - πL), meaning that with a probability (πL) Player B will play Left and with a probability (1 - πL) will play Right

• Player B is mixing over the pure strategies Left and Right

• The probability distribution (πL, 1 - πL) is a mixed strategy for Player B

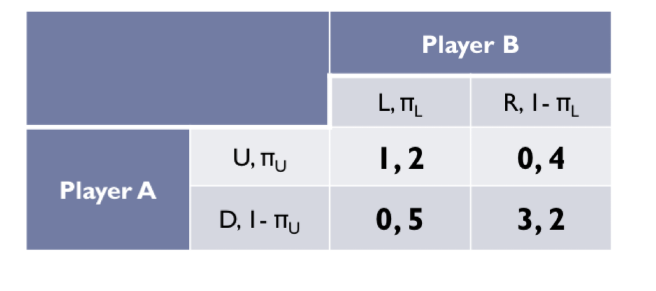
Step 1: solving for B

• What is the utility of Player B for just going to the Left?

  • Utility of Player B depends on the probability of Player A to go Up/Down → Getting 2 or 5 in utility

  • If B plays left, her expected payoff is: 2pU + 5(1 - pU)

    • Utility X probability

• What is the utility of Player B for just going to the Right?

  • Utility of Player 2 depends on the probability of Player A to go Up/Down → Getting 4 or 2 in utility

    • If B plays right, her expected payoff is: 4pU + 2(1 - pU)

Step 2: solving for B indifferent

• For a mixed strategy for a player, we need to see some probability distribution that makes the other player indifferent between his or her pure strategies:

  • If 2πu + 5(1- πu) > 4πu + 2(1- πu), player B would play Left

  • If 2mu + 5(1-πu) < 4πu + 2(1 - πu), player B would play Right

• So, for there to be an equilibrium, B must be indifferent between playing Left or Right i.e., we need to determine the threshold

  • 2πu + 5(1-πu) = 4πu + 2(1 - πu)

• Can you solve this?

  • 2πy +5 - 5πu = 4πu +2-2πu

  • 3πu+5=2πu+2

  • - 5πu= -3

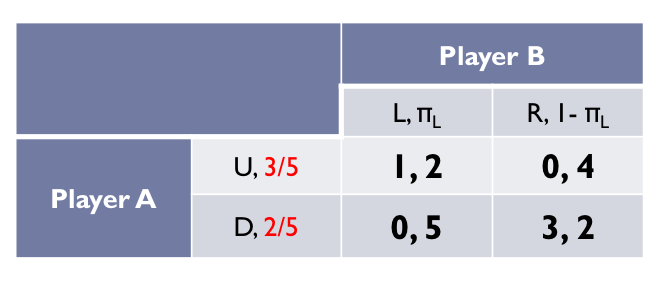
  • πu = 3/5

    • Up

  • 1 - πu = 2/5

    • Down

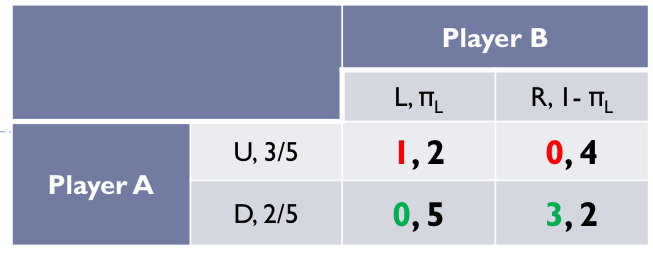
Step 3: solving for A

• What is the utility of Player A for just playing Up?

  • Utility of Player A depends on the probability of Player B to go Left/Right

  • If A plays Up, his expected payoff is: 1πL+ 0(1-πl) = πL

• What is the utility of Player A for just playing Down?

  • Utility of Player A depends on the probability of Player B to go Left/Right

  • If A plays Down, his expected payoff is : 0πL + 3(1-πL) = 3(1-πL)

Step 4: solving for A indifferent

• So, for there to be an equilibrium, A must be indifferent between playing Up or Down i.e., we need to determine the threshold

  • πL = 3(1-πL)

• Can you solve this?

  • πL = 3 - 3πL

  • 4πL = 3

  • πL =3,142 L 3/4

  • πL= 3/4

    • Left

  • 1 - πL = 1/4

    • Right

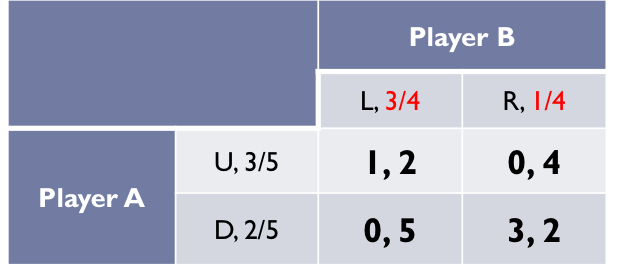
Step 5: MSNE

MSNE = (3/5, 2/5) (3/4, 1/4)

Alternative writing

• MSNE = (3/5U, 3/4L)

• MSNE = (3/5, 3/4)

NOTE: always write in fractions