Geo U2 - Basic Geo. & Segment/Angle Proofs

U2 How many planes can pass through 3 points?

If three points are collinear then infinite

If not collinear thsn one

U2Straight angle and supplementary angle

Straight angle = 180 degrees

Supplementary angle = two or more angles that ADD to 18-

U2Reflex angle

More than 180 and less then 360

U2Congruent

Two angles are congruent if and only if they have the same measure

U2 Perpendicular, right angles

Lines that form right angles

Right angles = 90 degrees

• in proofs, must have “right angle” and “definition of right angle” as separate rows

U2 Bisect

Cut into two congruent parts

U2 Negative Angles v positive

clockwise rotation, positive = counterclockwise

• by default = angles rotate counter clockwise

U2 Vertical angles

Angles across from each other, formed by two intersecting lines, congruent and therefore have the same measure

U2 Cogruent v Equal

Congruent is for shapes or lines Equal is for numbers or measures

U2 Angle

The union of 2 rays with a common endpoint called the vertex.

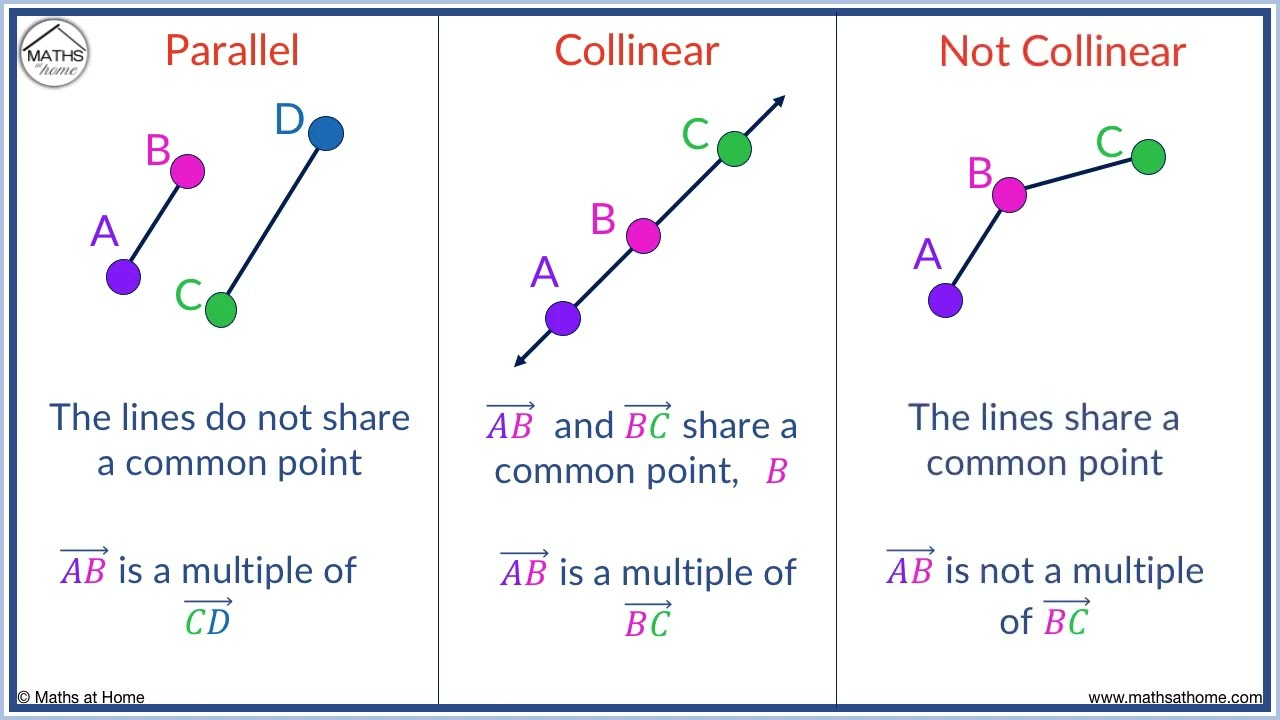
U2 Collinear

Points are collinear if and only if they are on the same line (one line COULD pass through them)

We need two points to determine a line becuase only one line can pass between two points , a line is the shortest path between two points, with only one point = INFINITE lines could pass through.

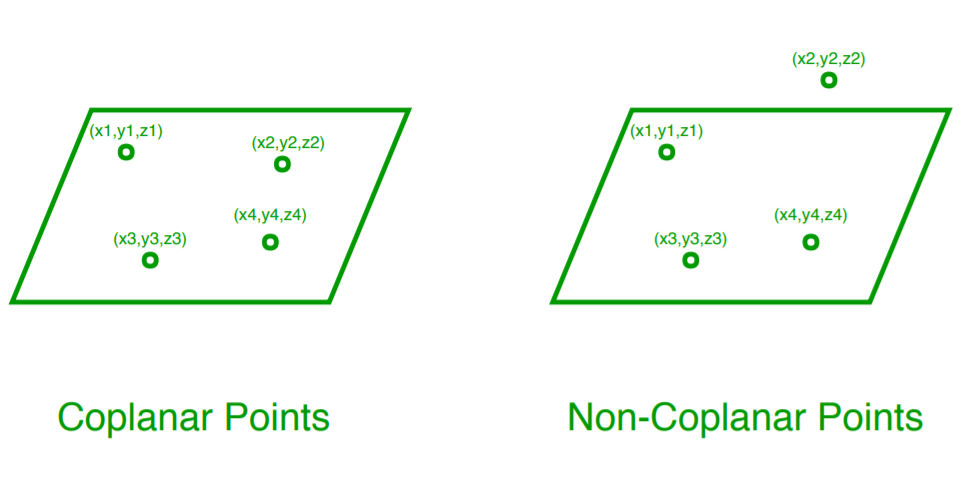
U2 Coplanar

Points or lines are coplanar if and only if one plane can pass through all of them.

• 3 (non collinear) points are needed to define a plane —> only one plane can go through all three

U2 Parallel lines, Midpoint

Parallel lines: on the same plane, meaning they are coplanar lines that never intersect

Midpoint: The point that divides a segment into 2 congruent parts

U2 Bisect

Cut into two congruent parts

U2 Skewlines

lines that are non coplanar

U2 Postulate/Axiom v theorems

A statement we accept WITHOUT proof

Theorems: a statement that needs to be proved

U2: Partition Postulate

The whole is the sum of its parts.

• may be used for angle measurments AND lengths

U2 What are the properties of congruence and what do each mean?

Reflexive: figure a is conguent to figure A

Symmetric: Figure A is congruent to fiure B then figure B is congruent to figure A

Transitive: if A is congruent to fig B and fig B is congruent to fig c then fig a is congruent to fig c

U2 Linear pairs (next to each other) v vertical pairs

Adjacent angles, are supplementary

Vertical: angles across from each other, are congruent

U2 When a way of light is reflected off of a flat surface, the angle of ——- is congruent to the angle of ——-.

Incidence and reflection

U2 Sphere

Collection of points that all have the same distance from a point in the center

U2 Symbols for geometry