Geometry Jurgensen Chapters 1-5, Geometry

a line that intersects two or more coplanar lines in different points

Transversal
(trans.)

two nonadjacent interior angles on opposite sides of a transversal

Alternate Interior Angles
(alt. int. ⦞)

two interior angles on the same side of a transversal

Same-side Interior Angles
(s-s. int. ⦞)

two angles in corresponding positions relative to the two lines

Corresponding Angles
(corr. ⦞)

parallelogram

A quadrilateral with both pairs of opposite sides parallel

Five ways to Prove that a quadrilateral is a parallelogram

1. Show that both pairs of opposite sides are parallel
2. Show that both pairs of opposite sides are congruent
3. Show that one pair of opposite sides are both congruent and parallel
4. Show that both pairs of opposite angles are congruent
5. Show that diagonals bisect each other

Rectangle

a quadrilateral with four right angles; is always a parallelogram

Rhombus

a quadrilateral with four congruent sides; is always a parallelogram

Square

A quadrilateral with four right angles and four congruent sides. Is always a rectangle, a rhombus, and a parallelogram.

Trapezoid

a quadrilateral with exactly one pair of parallel sides

Isosceles trapezoid

a trapezoid with congruent legs

Polygon

A closed geometric figure in a plane formed by connecting line segements endpoint to endpoint with each segment intersecting exactly two others. No tow segments with a common endpoint are collinear.

Convex polygon

a polygon such that no line containing a side of the polygon contains a point in the interior of the polygon

Diagonal

a segment that joins two nonconsecutive vertices

Regular polygon

a polygon that is both equilateral and equiangular

Triangle

figure formed by 3 segments joining 3 noncollinear points

Vertex of triangle

each of the 3 points joining the sides of a triangle

Sides of triangle

the sides of a triangle are the segments that make up the triangle

Vertices

plural of vertex

Scalene triangle

a triangle with no congruent sides

Isosceles triangle

A triangle with at least two congruent sides

Equilateral triangle

a triangle with all sides congruent

Acute triangle

A triangle with three acute angles

Obtuse triangle

a triangle with one obtuse angle

Right triangle

a triangle with one right angle

Equiangular triangle

a triangle with all angles congruent

Auxiliary line

line (or ray or segment) added to a diagram to help in a proof; *shown as a dashed line

Remote interior angles

the two nonadjacent interior angles corresponding to each exterior angle of a triangle

Exterior angle

an angle formed by one side of a triangle and the extension of another side

Postulate 11

if two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel

Parallel lines

coplanar lines that do not intersect

Parallel planes

planes that do not intersect

Alternate interior angles

two nonadjacent interior angles on opposite sides of the transversal; (to find alternate interior angles, look for the letter "Z" or backwards "Z")

Same-side interior angles

two interior angles on the same side of the transversal; (to find same-side interior angles, look for a square "C" or backwards square"C")

Corresponding angles

two angles in corresponding positions relative to the two lines; (To find corresponding <'s, look for the letter "F" or backwards "F, or upsidedown "F")

Median of a triangle

A segment from a vertex to the midpoint of the opposite side

Altitude of a triangle

the perpendicular segment from a vertx to the line containing the opposite side

Perpendicular bisector of a segment

a segment, ray, line, or plane that is perpendicular to a segment at its midpoint

hypotenuse

the side of a right triangle opposite the right angle

Leg-Leg Method (LL)

If two legs of one right triangle are congruent to the two legs of another right triangle, then the triangles are congruent.

Hypotenuse-Acute Angle Method (HA)

If the hypotenuse and an acute angle of one right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the triangles are congruent.

Leg-Acute Angle Method (LA)

If a leg and an acute angle of one right triangle are congruent to the corresponding parts in another right triangle, then the triangles are congruent.

SSS Postulate

if three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent

SAS Postulate

if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent

ASA Postulate

if two angles and the included side of one triangle are congruent to two angles and the included side of the second, the triangles are congruent

Congruent triangles

Two triangles are congruent if and only if their vertices can be matched up so that all of their corresponding parts (sides and angles) are equal

Congruent polygons

Two polygons are congruent if and only if their vertices can be matched up so that their corresponding parts are congruent.

Non coplanar

Not in the same plane

Equidistant

equally distant from two points

set of all points

Space

Undefined terms

Point, line, plane

Collinear

lying on the same line

Coplanar

lying in the same plane

then their intersection is a line.

If two planes intersect,

Through any two points there is

Exactly one line

two

A line contains at least ____ points. (a)

set of points that are in both figures

Intersection

four

Space contains at least ____ points, not all in the same plane. (a)

then the line that contains the points is in that plane.

If there are two points in a plane,

distance between two points;
found by taking the absolute value of the difference of the coordinates of the two points

Length (distance is always positive)

there is at least one plane.

(c) Through any three points

the number that is paired with a particular point on a number line

Coordinate

three

A plane contains at least ____ points, not all in one line. (a)

Through any three non collinear points there is

Exactly one plane. (If the points are collinear, then an infinite number of planes might intersect them.)

If two lines intersect then

Exactly one plane contains the lines

point that divides the segment into two congruent segments

Midpoint
(midpt.)

a line, ray, or plane that intersects the segment at its midpoint

Definition of a Segment Bisector

Ray

A straight line extending from a point

two rays that have the same endpoint, and the endpoint lies between the two second points

Opposite Rays

Angle

Consists of two rays (sides) and a common endpoint (vertex).

angle with measure greater than 90° and less than 180°

Obtuse Angle

Acute angle

an angle less than 90 degrees but more than 0 degrees

angle with measure of 180°

Straight Angle

angles that have equal measures

Congruent Angles
(≅ ⦞)

unique positive number ≤ 180° that is paired with the angle

Measure of an Angle
(m∠)

two objects that have the same size and shape

Congruent
(≅)

Right angle

an angle that measures 90 degrees

a ray that divides an angle into two congruent adjacent angles

Definition of an Angle Bisector (the smaller parts are equal to EACH OTHER)

segments that have equal length

Congruent Segments
(≅ seg.)

Congruent angles

angles that have the same measure

Adjacent angles

are a pair of angterm-19les with a common vertex and a common side, but no common interior points

Postulate

A statement that can be taken as fact without being proven.

1. The points on a line can be paired with the real numbers in such a way that any two points can have coordinates 0 and 1.
2. Once a coordinate system has been chosen this way, the distance between any two points equals the absolute value of the differencde4 of their coordinates.

Ruler Postulate

If B is between A and C, then:
AB + BC = AC.

Segment Addition Postulate

On line AB in a given plane, choose any point O between A and B. Consider ray OA and ray OB and all other rays that can be drawn on one side of line AB. These rays can be paired with the real numbers from 0 to 180 in such a way that:

a. ray OA is paired with 0 and ray OB with 180.
b. If ray OP is paired with x, and ray OQ is paired with y, then
m ∠ POQ = Ιx-yΙ

Protractor Postulate

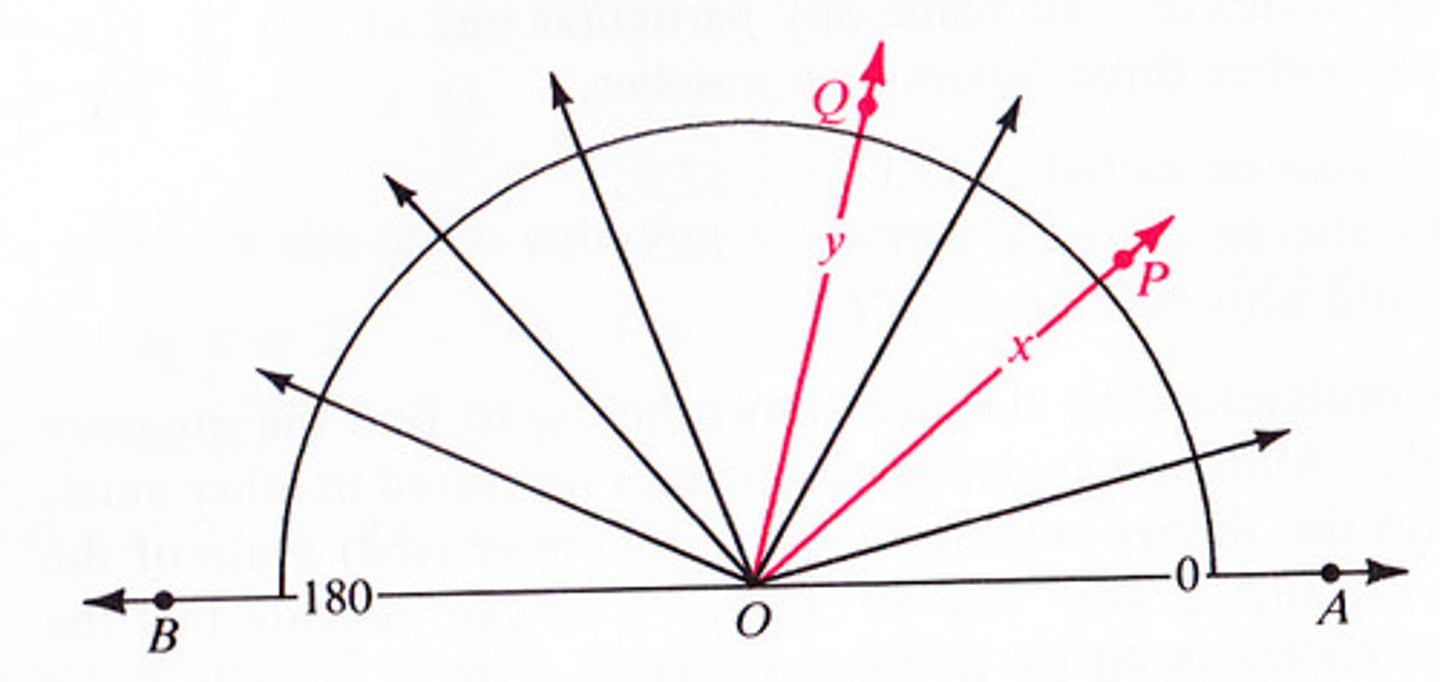
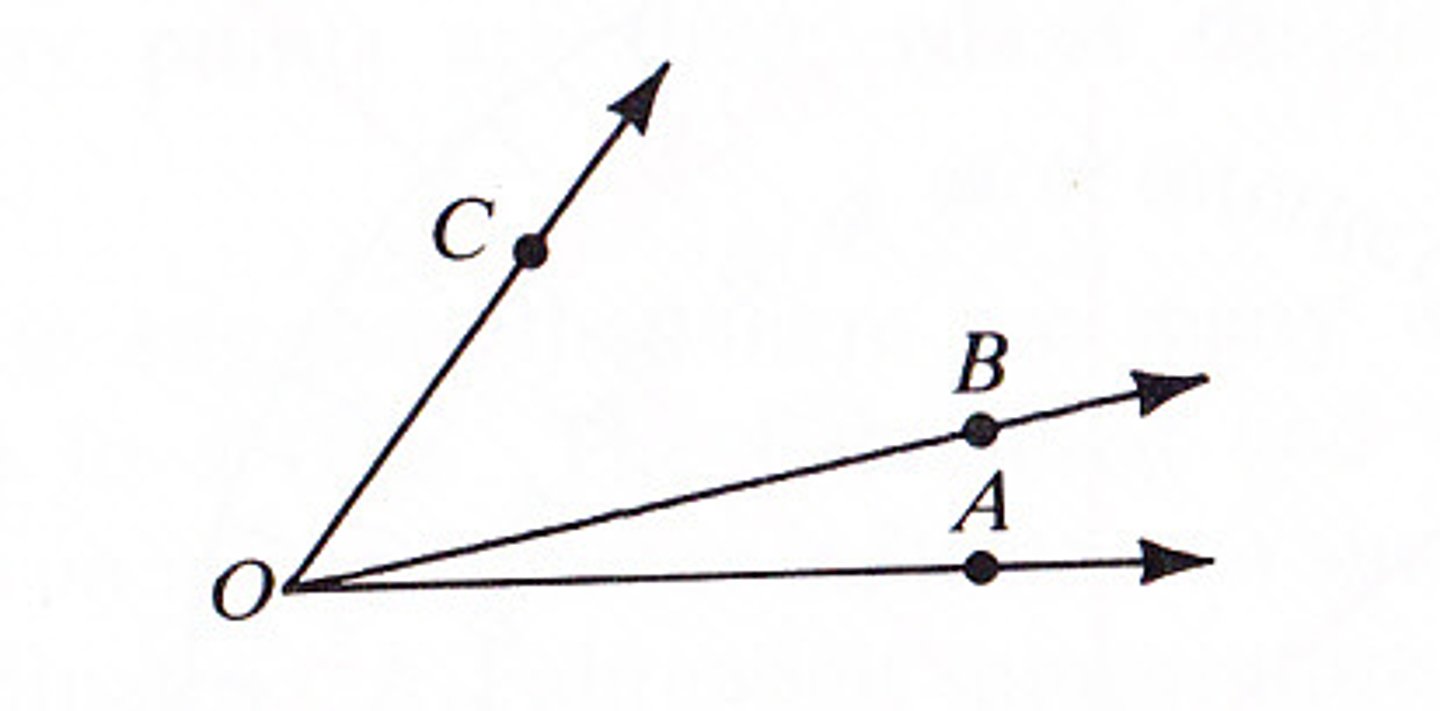
If point B lies in the interior if ∠AOC then
m∠AOB + m∠BOC = m∠AOC.

Angle Addition Postulate - part 1

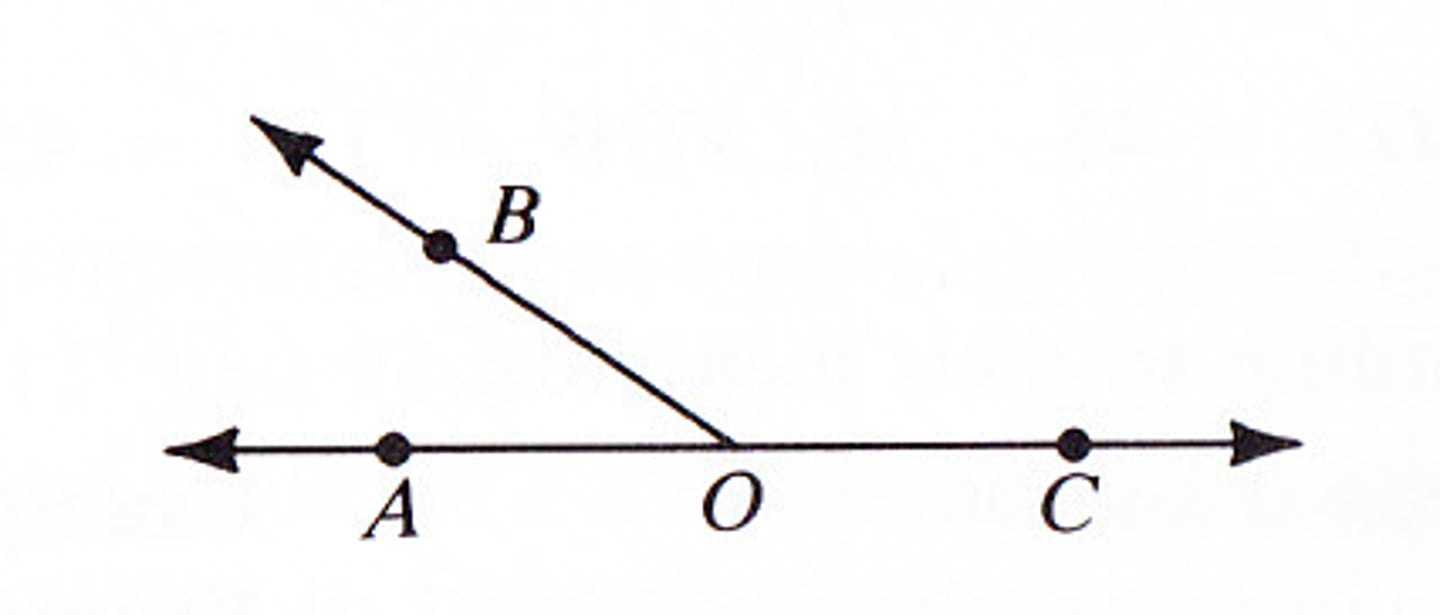
If ∠AOC is a straight angle and B is any point not on line AC, then
m∠AOB + m∠BOC = 180

Angle Addition Postulate - part 2

If line segment DE ≅ line segment FG, then
line segment FG ≅ line segment DE.

If ∠ D ≅ ∠ E, then
∠ E ≅ ∠ D.

Symmetric Property (properties of congruence)

If line segment DE ≅ line segment FG and line segment FG ≅ line segment JK, then
line segment DE ≅ line segment JK.

If ∠ D ≅ ∠ E and ∠ E ≅ ∠ F, then
∠ D ≅ ∠ F.

Transitive Property (properties of congruence)

a(b+c) = ab + ac

Distributive Property (algebra - properties of equality)

an angle that makes another angle total 90°

Complement
(comp.)

two angles whose measures have the sum 90°

Complementary Angles
(comp. ⦞) (Do not need to be adacent)

coplanar lines that do not intersect

Parallel Lines
(∥ lines)

planes that do not intersect

Parallel Planes
(∥ planes)

lines, rays, or segments that intersect to form right angles

Perpendicular
(⊥)

an angle that makes another angle total 180

Supplement
(supp.)

two angles whose measures have the sum 180°

Supplementary Angles
(supp. ⦞) (Do not need to be adjacent)

Addition Property of Equality

If you add the same number to each side of an equation, the results are equal; If A = B, then A + C = B + C

Subtraction Property of Equality

If you subtract the same number from each side of an equation, the two sides remain equal; If A = B, then A - C = B - C

Multiplication Property of Equality

If you multiply each side of an equation by the same number, the two sides remain equal; If A = B, then AC = BC