Theoretical CS Final Exam

What is a DFA?

A computational model for a simple computer

What is the formal definition of a DFA

A five-tuple (Q, ∑, ∂, q_o, F) where:

\
Q: finite set of states

∑: finite alphabet

∂: transition function - Q x ∑ → Q

q_0: start state

F: final state

Define a Regular Language (using DFA).

A language is regular if there exist some DFA that recognizes it

What are the Regular Operations?

Union, Star, Concatenation

What does it mean to be closed under an operation?

If A1 and A2 are regular languages, then the result of the regular operation of those two is itself another regular language.

\
example: union

If A1 and A2 are regular languages, then A1 U A2 is a regular expression

How do we prove that a regular language is closed under the regular operations?

Proof by construction. Construct the resulting DFA

What other operations are regular languages closed under?

Intersection and Complement

What is the formal definition of an NFA?

five-tuple (Q, ∑_(e), ∂, q_o, F) where:

\
Q: finite set of states

∑: finite alphabet (including empty string)

∂: transition function (Q x ∑_(e) → P(Q)

q_o: start state

F: accept state

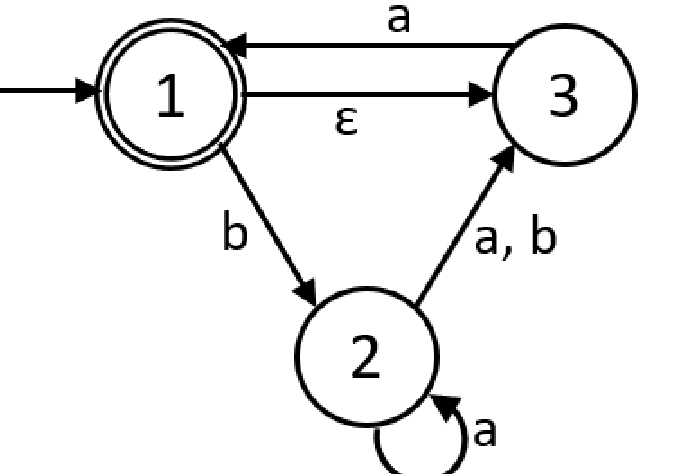
Given the NFA, perform the NFA to DFA algorithm.

Prove that a language is regular if a NFA recognizes it.

Every NFA can be convert to an equivalent DFA. A language is regular if theres a DFA to recognize it, therefore, if there exist an NFA to recognize the language, then it is regular.

Describe the steps to show the union of two NFAs.

Create a new start state

Create e-transitions from the new start state to the former start states of the two machines

Describe the steps to show the concatenation of two NFAs.

Create an e-transition from the final state of A to the start state of B

Remove the final state from A

Describe the steps to show the star of an NFA.

Create a new start state

Create e-transition from the new start state to the former start state

Create e-transitions from all final states to the original start state

Make the new start state a final state (empty string)

What are Regular Expressions?

A text-based method to define exactly what strings are included in a language (using the regular operations)

What language does the regular expression b∑\* *U ∑*\*a generate?

All strings that start with a ‘b’ OR end with an ‘a’

\
(∑\* means a U b any number of times)

Write these regular expression.

Define a regular language (using RE).

A language is regular if there’s some regular expression that describes

Convert this RE to an NFA.

\
ab(bb)\*a

Describe the DFA to RE algorithm

1. Add new start state with an e-transition to the former start state
2. Add a final state with an e-transition from the former final states (no longer final)
3. One state at a time, convert to RE using the regular operations

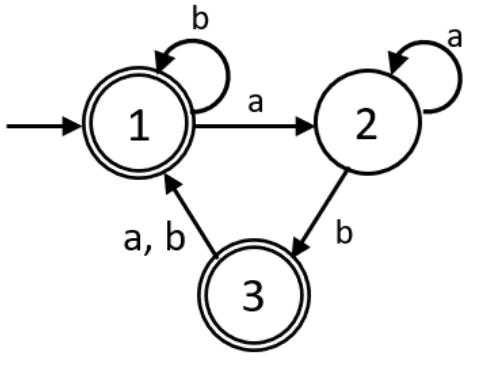
Given the DFA, perform the DFA to RE algorithm.

DFA union.

DFA intersection.

For Regular Languages, what is the language generator and what is the language recognizer?

Regular expression (generator)

DFA (recognizer)

For Context-Free languages, what is the language generator and what is the language recognizer?

CFG (generator)

PDA (recognizer)

What is the formal definition for a context-free grammar?

G = (V, ∑, R, S) where:

\
V: finite set of variables

∑: finite set of terminals

R: set of rules

S: starting variable

Create a context free grammar for aªbª (a = n)

Create a parse tree for the aªbª

Show the leftmost derivation for aªbª

What is ambiguity?

If there exists more than one leftmost derivation or parse trees for the same string

Common CFG builds

Formally define the union of two CFGs

G = (V1 U V2 U {S}, ∑, R1 U R2 U {S → S1 | S2}, S) and V1 ∩ V2 = 𝝓

Formally define the concatenation of two CFGs

G = (V1 U V2 U {S}, ∑, R1 U R2 U {S → S1 S2}, S) and V1 ∩ V2 = 𝝓

Formally define the star of a CFG

G = (V1 U {S}, ∑, R1 U {S → S1 S, S → 𝜺}, S)

Describe the steps of converting to Chomsky Normal Form.

1. Add new start variable
2. Remove e-rules
3. Remove unit rules
4. Clean up

Under what conditions does a PDA accept a string?

All input is consumed

On a final/accept state

Stack is empty

What is the form of a transition for PDA?

input, pop → push

What is the formal definition of PDA?

A six-tuple (Q, ∑, ∫, ∂, q_0, F) where:

\
Q: finite set of states

∑: input alphabet

∫: stack alphabet

∂: transition function (Q x ∑_e x ∫_e → P(Q x ∫_e)

q_0: start state

F: final state

Build PDAs

Describe the Big Loop algorithm/

Push $: e, e → $

On loop:

* Terminals (t): t, t → e
* Rules (R → w): e, R → w

Pop $: e, $ → e

What is the form of the transition of a Turing Machine?

input → write, direction

What is the formal definition of a Turing Machine

What is a configuration of a TM and what does it consist of?

A snapshot of where the TM is at, at a given time in its computation

\
Current state

Current tape content

Location of tape head

\
example:

(q5, abbaa)

What is T-decidable?

What is T-recognizable?

Build TM

Copy function of TM

Right shift function of TM

Left shift function of TM

TM variants:

Stay

Doubly infinite

Multi-tape

Multi-head

Nondeterministic

What operations are T-decidable languages closed under?

Union, Concatenation, Star, Intersection, Complement

What is the time complexity for converting a Multi-tape TM to a Single-tape TM?

Squares the time

What is the time complexity for converting a Non-deterministic TM to a deterministic TM?

What operations are T-recognizable languages closed under?

Union, Concatenation, Star, Intersection

What was The Church-Turing Thesis, 1936?

Any TM that halts on all inputs (a decider) is considered an algorithm and any algorithm can be rendered as a TM that halts on all inputs

A string compatible way to represent a graph

Listing (, ) where V is the nodes or vertices and E is the edges

What does the acceptance problem for DFAs ask?

Define.

Is it T-rec or Decidable?

Does a particular DFA accept (decide) a given string?

\
On input

Define acceptance problem for NFA

Is it T-rec or Decidable?

On input

Define acceptance problem for Regular Expression

Is it T-rec or Decidable?

On input

Define acceptance problem for Turing Machine

\
Is it T-rec or Decidable?

On input

How to prove ATM is not decidable?

Assume ATM is decidable, then obtain a contradiction

What is the Halting Problem?

What is a co-Turing-Recognizable language

The complement of a T-recognizable language

True or False

If A is reducible to B (A < B) and B is decidable, then A is decidable

True

Prove by contradiction that HALT_TM is undecidable

Assume Halt is decidable and TM R decides it.

Build TM S to decide ATM

S = on input

Definition for time complexity

M is a function ƒ: N → N, where ƒ(n) is the maximum number of steps that M uses on any input of length n.

\
n represents the length of the input

ƒ(n) is the running time of M (runs in time ƒ(n)

Define time complexity classes

TIME(t(n)) to be the collection of all languages that are decidable by an O(t(n) time Turning Machine

Time Complexity Estimation:

Scan across tape 1; reject if an a symbol is found to the right of a b symbol

O(n)

Time Complexity Estimation:

Scan across the a’s on tape 1 until the first b. At the same time, copy the a’s onto tape 2

O(n)

Time Complexity Estimation:

If all the a’s have been crossed off, accept. If any a’s remain, reject

O(1)

Time Complexity Estimation:

Repeat while both a’s and b’s remain on the tape

Scan the tape, crossing off exactly one a and exactly one b

O(n^2)

\
The outer loop is O(n/2)

The inner loop is O(n)

\
O(n/2 • n) = O(n^2)

Time for conversion to single tape TM from multi-tape TM

O(t^2(n)

\
Squares the time

\
Can be done in n log n time but squared is guarenteed

Running time for non-deterministic TM

Maximum height of tree - (ƒ(n))

Time for conversion to Deterministic Single Tape TM from Non-deterministic (any tape) TM

b^(O((t(n)))

What is the traveling salesman problem?

Given a list of cities and distances between each pair of cities. What is the shortest possible route that visits each city exactly once and returns to the origin city?

What is the time complexity for the traveling salesman problem?

O(n!) - factorial

\
There is a known exponential solution using dynamic programming

Define Eulerian Path

M = on input

What is the running time of Euler path?

Polynomial

What’s the difference between an Eulerian path and Hamiltonian path?

An eulerian path reaches every edges exactly once whereas a hamiltonian path reaches every vertex exactly once

What is the running time for Hamiltonian path?

Exponential

What is P?

The class of languages decidable in polynomial time on a deterministic single tape TM

What does P roughly correspond to?

The class of languages that are realistically solvable (decidable) on a computer

Define the algorithm for PATH

M = on input

What is the time complexity class of PATH

Polynomial

FSA Algorithms time complexity:

1) RE → NFA

2) NFA → DFA

3) Minimize a DFA

4) DFA isomorphism

5) A_dfa

6) DFA → RE

1) Polynomial

2) Exponential

3) Polynomial

4) Polynomial

5) Polynomial

6) Exponential

What is the time complexity class of HAMPATH

Exponential

\
No known polytime solution

What can we do in polynomial time with HAMPATHS?

We can verify it in polynomial

Define a verifier

Algorithm V where A = {w | V accepts

What is a certificate?

The alleged solution (string) used to verify

\
For HAMPATH, the certificate would be a hamilitonian path from s to t

\
Has to have polynomial length or less

Define polynomially verifiable.

A language is polynomially verifiable if it has a polytime verifier

What is the HAMPATH Complement?

If there is NO hamilitonian path

What is a clique? What time complexity class is it in? Is it polynomially verifiable?

A clique is a subset of vertices within a graph where every vertex in the subset is connected to every other vertex in the subset. (complete sub-graph)

\
Exponential

\
Yes, it is poly-time verifiable

What is an independent set? What time complexity class is it in? Is it polynomially verifiable?

A sub-graph where no two nodes are connected by an edge

\
Exponential

\
Yes, it is poly-time verifibale

What is a vertex cover? What time complexity class is it in? Is it polynomially verifiable?

a subset of vertices in a graph that "cover" all the edges in the graph.

\
Exponential

\
Yes, it is poly-time verifiable

What is the Subset Sum problem? What time complexity class is it in? Is it polynomially verifiable?

Given a multi-set of integers, and a target number, is there some way to pick a subset of those integers that adds up to the target

\
Exponential

\
Yes, it is poly-time verifiable

What is the partition problem?

Given a multi-set of integers, split into two parts where one part contains a sum of the integers equal to the sum of the other part’s sum

\
Exponential

\
Yes, it is poly-time verifiable

\
(1, 8, 3, 2, 5, 1)

Group 1: (8, 2) = 10

Group 2: (1, 3, 5, 1) = 10

What is the 2-machine scheduling problem?

Given a set of process times and D, a deadline, does there exist a way to schedule the k processes on 2 machines within the deadline

\
Exponential

\
\

What is the SAT problem?

Given a boolean formula, is there a variable combination that evaluates as true

\
Exponential (truth table -- 2^n)

What is a literal?

A boolean variable or negated boolean variable

What is a clause?

Several literals connected with ORs

What is Conjuctive Normal Form?

Several clauses ANDed together

What is 3-CNF?

All clauses have 3 literals

What is 3-SAT problem? What is

Is there a way to assigned values to variable to something in 3CNF such that the formula is true?