AP Calculus AB Exam Review

AP Calculus AB Exam Review Flashcards

When does a limit exist?

Exists if and only if the limit from the left equals the limit from the right equals the limit at that point.

Definition of Continuity

A function is continuous at x = a if and only if f(a) exists, the limit as x approaches a of f(x) exists, and f(a) = limit as x approaches a of f(x).

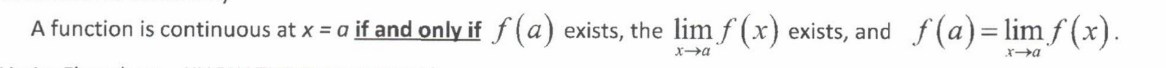
Intermediate Value Theorem

If y = f(x) is continuous on its closed interval [a, b] and N represents a number that occurs between f(a) and f(b), then there exists some number c in (a, b) such that f(c) = N as long as f(a) ≠ f(b).

(The IVT is just saying that a continuous function must intersect every y-value on the interval)

Formal Definition of a Derivative

The slope of the tangent line to a function at any point is m = limit as h approaches 0 of [f(x+h) - f(x)] / h.

Point-Slope Form

y - y₁ = m(x - x₁)

When is an object speeding up?

An object is speeding up when its velocity and acceleration have the SAME SIGN.

When is an object slowing down?

An object is slowing down when its velocity and acceleration have DIFFERENT SIGNS.

Linear Approximation

If the point of tangency is (a, f(a)), then f(x) ≈ f(a) + f'(a)(x - a).

Derivative of the Inverse Function

(f⁻¹)'(a) = 1 / f'(f⁻¹(a))

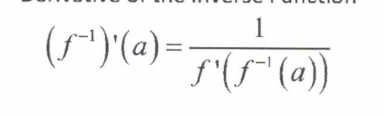
Mean Value Theorem

If y = f(x) is continuous on its closed interval and differentiable on its open interval, then there exists some number "c" on its open interval (a, b) such that f'(c) = [f(b) - f(a)] / [b - a]

The MVT is saying that there must be at least one point between “a” and “b” where the slope of the tangent line is the same as the slope of the secant line

Displacement

The displacement (location) of an object equals the area under the curve from the location where the object started (a) to where it ended (b)

Distance Traveled

The distance traveled by an object equals the absolute value of the area under the curve from the location where the object started (a) to where it ended (b). To calculate distance traveled, break integrals into periods of positive velocity and negative velocity; then, add the integrals together.

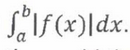
The Fundamental Theorem of Calculus

g(x) = ∫f(t)dt from a to x AND g'(x) = f(x)

Average Value of a Function

[1 / (b - a)] ∫f(x)dx from a to b, if f(x) is continuous on [a, b]

Solving a Differential Equation

To solve a differential equation, you MUST separate the variables, then integrate both sides of the equation.

Slope Fields

Sketch in the particular solution using the tangent line; do NOT extend the slope field past the borders or past asymptotes of the particular solution

Areas Between Curves

A = ∫[f(x) - g(x)]dx from a to b OR A = ∫[f(y) - g(y)]dy from c to d

Volume of a Solid (Disk)

A disk is created when there is no space between the area that is being revolved and the axis about which it is being revolved around. AREA OF A DISK = πr²

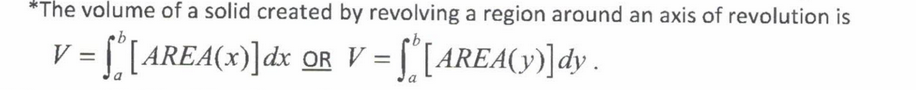
Volume of a Solid (Washer)

A washer is created when there is space between the area that is being revolved and the axis about which it is being revolved around. AREA OF A WASHER = πR² - πr²

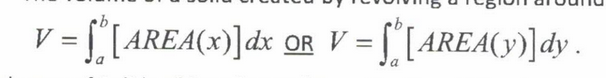
Volume of Solids of Revolution (Cross Sections)

The area of each cross-sectional slice is found by finding the area of each 2-dimensional figure. To find the volume, you have to integrate the area of the figures as stacked from left to right (in terms of “x”) or bottom to top (in terms of “y”)

Limit Law: Sum

lim [f(x) + g(x)] = lim f(x) + lim g(x)

Limit Law: Difference

lim [f(x) - g(x)] = lim f(x) - lim g(x)

Limit Law: Constant Multiple

lim [cf(x)] = c lim f(x)

Limit Law: Product

lim [f(x) * g(x)] = lim f(x) * lim g(x)

Limit Law: Quotient

lim [f(x) / g(x)] = lim f(x) / lim g(x), if lim g(x) ≠ 0

Limit Law: Power

lim [f(x)]^n = [lim f(x)]^n

Limit Law: Constant

lim c = c

Limit Law: Identity

lim x = a

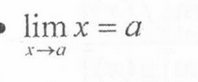
Limit Law: Power Function

lim x^n = a^n

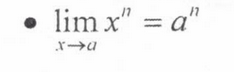
Limit Law: Root Function

lim √x = √a

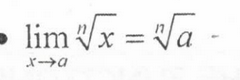
Limit Law: nth Root of a Function

lim n√f(x) = n√lim f(x)

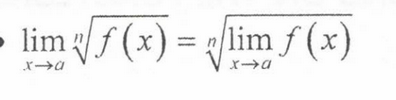
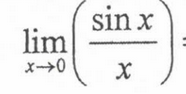
1

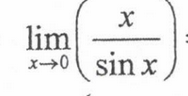
1

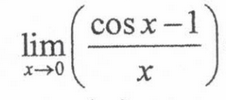
0

Factoring Cubes x³ + y³

(x + y)(x² - xy + y²)

Factoring Cubes x³ - y³

(x - y)(x² + xy + y²)

Double Angle Identity: sin 2x=

2 sin x cos x

Double Angle Identity: cos 2x=

cos²x - sin²x = 2 cos²x - 1 = 1 - 2 sin²x. It equals all 3 of these. Must memorize all 3.

Pythagorean Identity: sin² x + cos² x =

sin² x + cos² x = 1

The Intermediate Value Theorem (IVT)

if a continuous function, f, with an interval [a,b] as its domain takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b) at some point within the interval.

AREA

the amount of space covered by a flat 2-D figure; write answers as units²

Perimeter

add the measures of all of the sides

Area of a Rectangle/Square

A = lw

SURFACE AREA

the amount of space consumed on the surfaces of a 3-D solid; write answers as units²

B

Area of the base

Formula for an exponential function into a logarithmic function

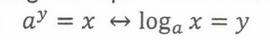
Rolle's Theorem

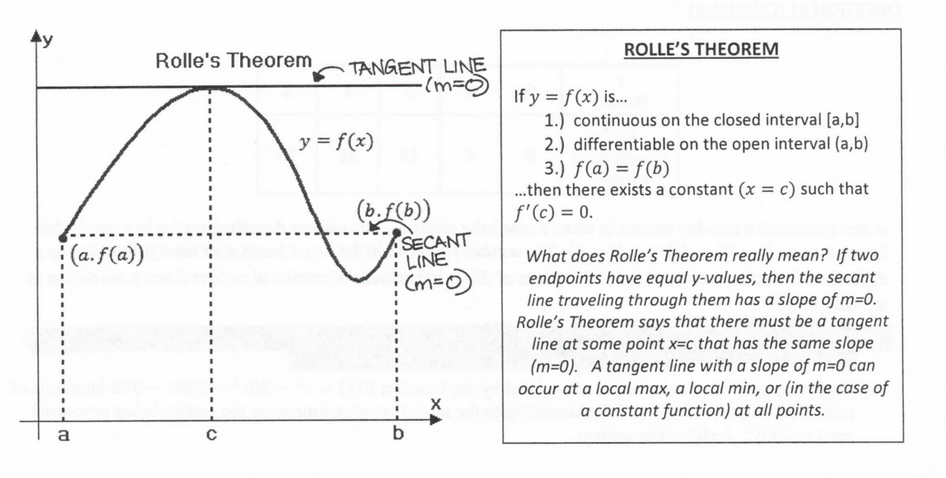
Mean Value Theorem

Point of Inflection

Switch in concavity

f'(c)=0 and f(x) is concave up at c

f(x) has a minimum at c

f'(c) =0 and f(x) is concave down at c

f(x) has a maximum at c

f'(x) = DNE

HOLE or VERTICAL ASYMPTOTE

INTEGRATION

the process of adding up an infinite number of objects under a curve

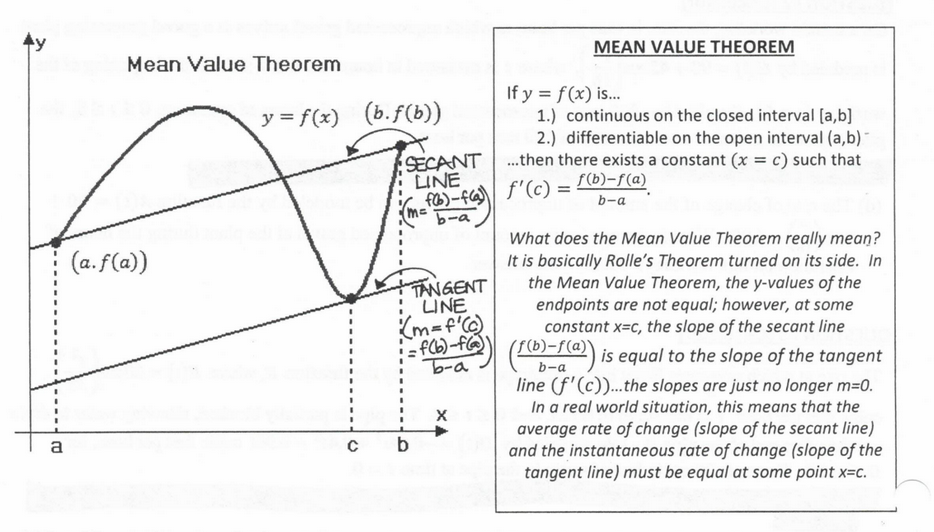
Riemann Sums

DISPLACEMENT:

the distance that an object is from its start point when it has finished moving

DISTANCE:

the amount of area that has been covered/accumulated in either the forward or backward direction

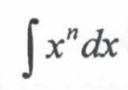
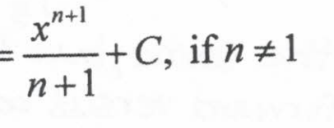
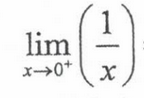
infinity

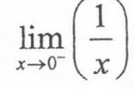
negative infinity

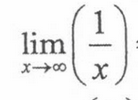
0

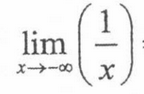
0

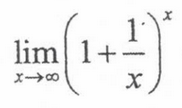
e

Pythagorean Identity: tan²x + 1 =

sec²x

Pythagorean Identity: 1 + cot²x =

csc²x

Derivative of a Constant:

0

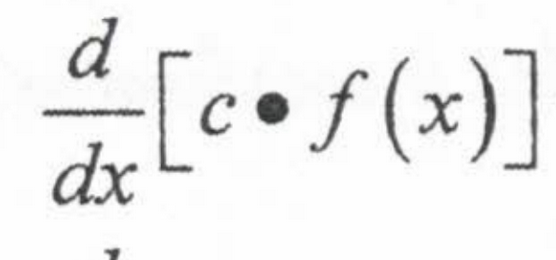
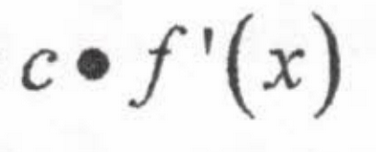
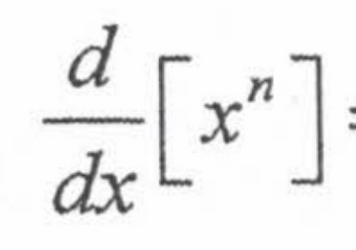
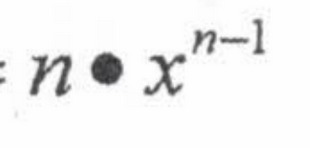
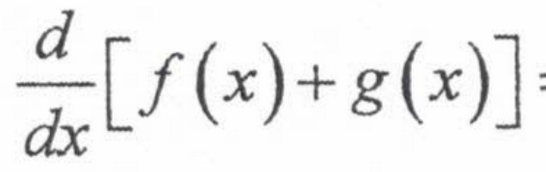
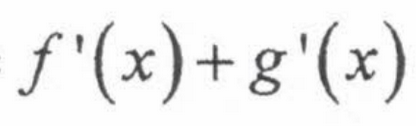
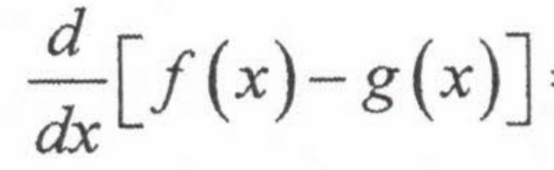
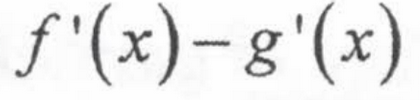
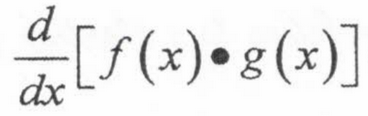
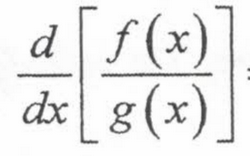
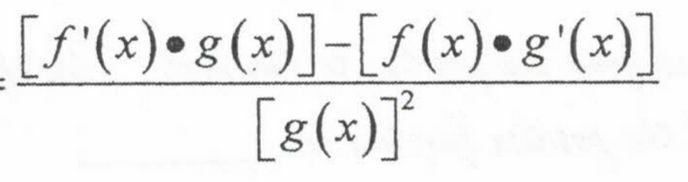
Derivative of sin(x)

cos(x)

Derivative of cos(x)

-sin(x)

Derivative of tan(x)

sec²x

Derivative of csc(x)

-csc(x)* cot(x)

Derivative of sec(x)

sec(x)tan(x)

Derivative of cot(x)

-csc²x

Derivative of inverse sin

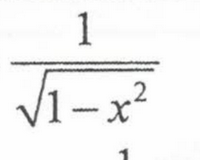
Derivative of inverse cos

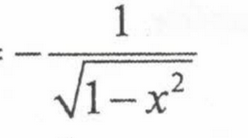
Derivative of tan

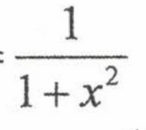
Derivative of csc

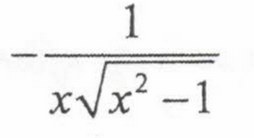
Derivative of inverse sec

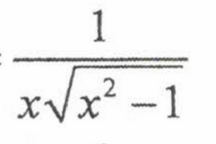
Derivative of inverse cot

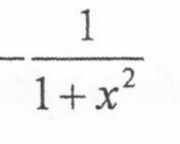
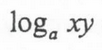
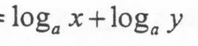
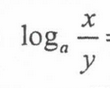
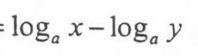
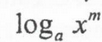
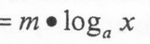
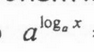
x

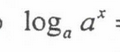
x

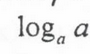
1

Change of Base Formula

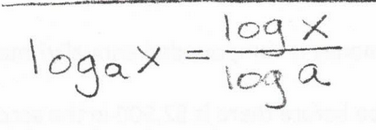
csc(x)

1/(sin(x)

sec(x)

1/cos(x)

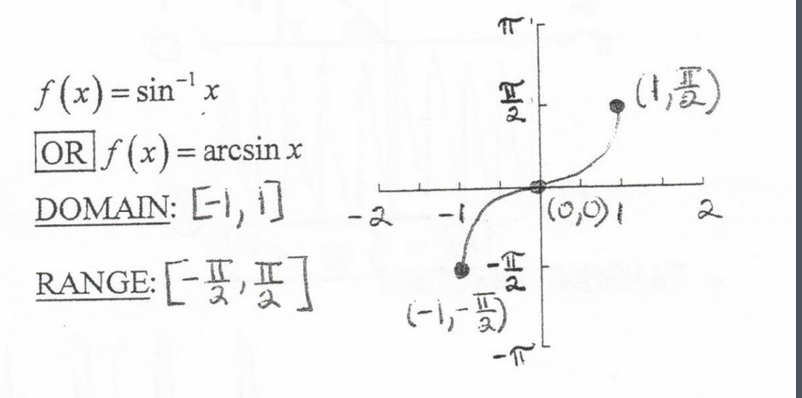
Domain and Range of inverse sin

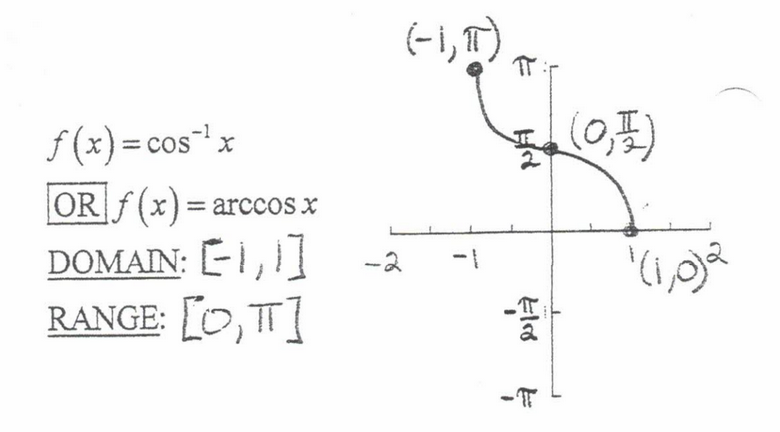
Domain and Range of inverse cos

A rational function has a vertical asymptote when:

The denominator but not the numerator is 0

A rational function has a hole when:

You can cancel a term from the numerator and denominator OR when plugging in a value gives 0/0

A rational function has a horizontal asymptote when:

When the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y=0

When the degree of the numerator and denominator are equal, the horizontal asymptote is at the (leading coefficient of the numerator/ leading coefficient of the denominator)

When the degree of the numerator is greater than that of the denominator, there is no horizontal asymptote