AP Calc BC/Calc 1 and 2 Flashcards

What must be true to use the Intermediate Value Theorem

The function must be continuous on the given interval. (Chap 1)

Justification statement for the Intermediate Value Theorem

By the intermediate value theorem, there exists a value c between a and b such that f(c)=k (Chap 1)

Product rule formula

(Chap 5)

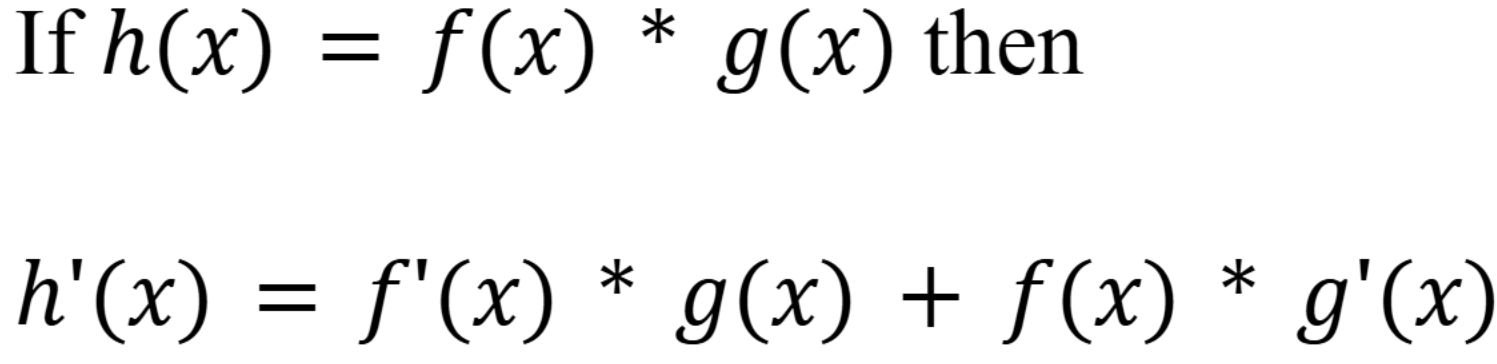
Quotient rule formula

(Chap 5)

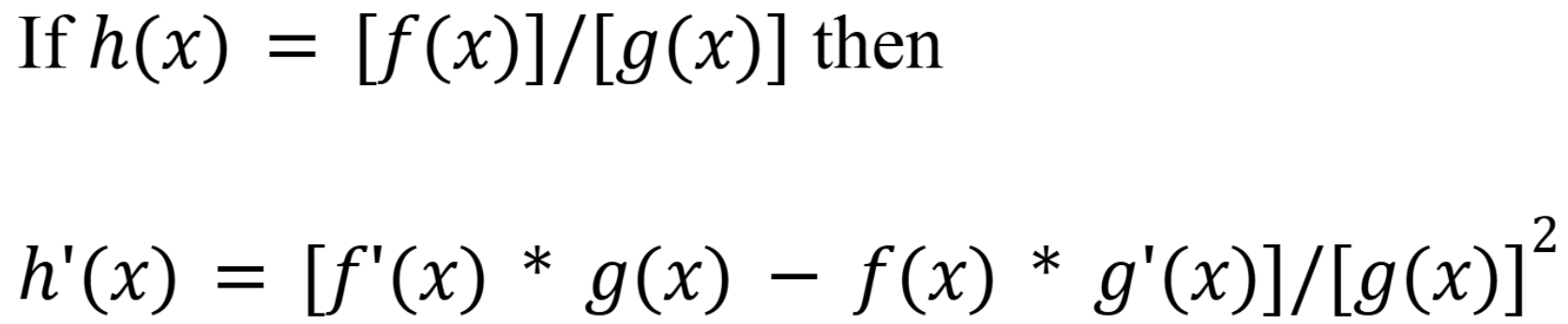
Derivative of tanx

(tanx)’ = sec²x (Chap 5)

Derivative of cscx

(cscx)’ = -cscxcotx (Chap 5)

Derivative of secx

(secx)’ = secxtanx (Chap 5)

Derivative of cotx

(cotx)’ = -csc²x (Chap 5)

Derivative of exponentials

(Chap 6)

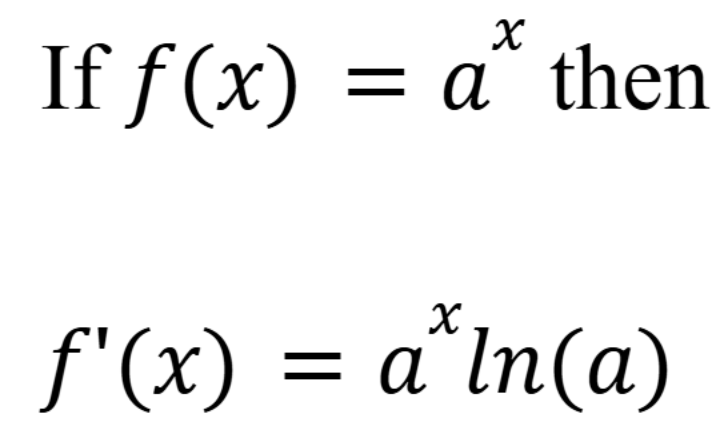
Integrals of exponentials

(Chap 6)

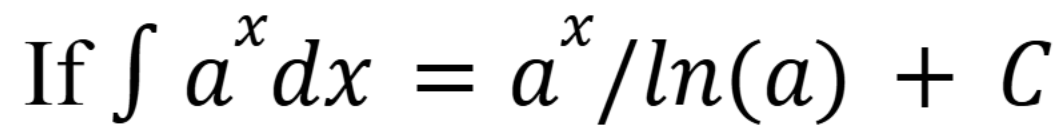
Derivative of sine inverse

(Chap 6)

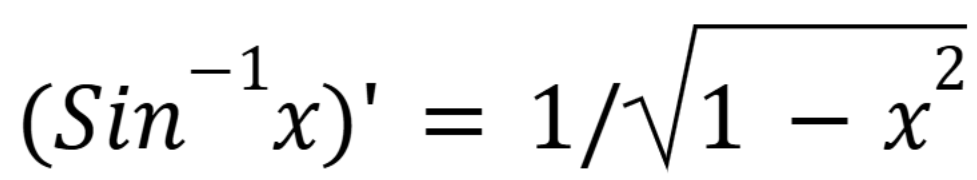
Derivative of cosine inverse

(Chap 6)

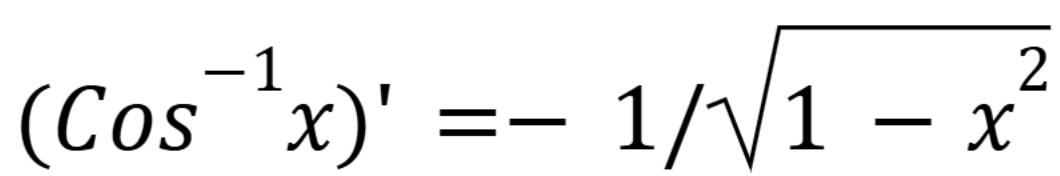
Derivative of tangent inverse

(Chap 6)

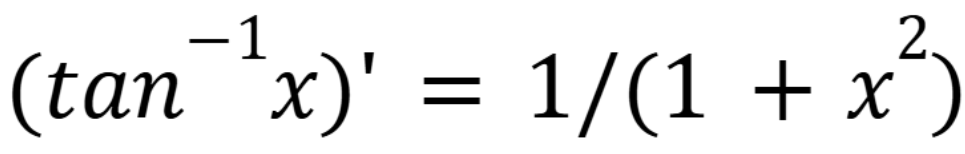
Derivatives of inverse functions

(Chap 6)

Arc Length formula

(Chap 7 I think)

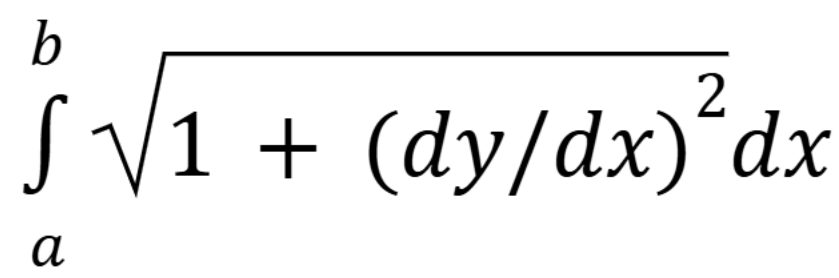
Integration by parts formula

(Chap 7 I think)

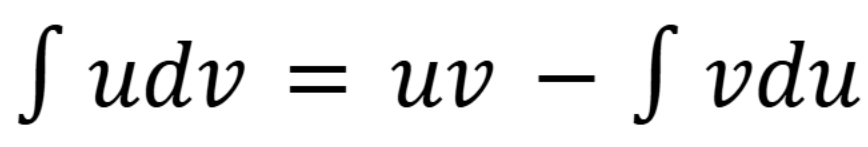
Trig-sub formulas

(Chap 7 I think)

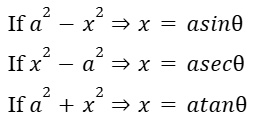
Washer formula

(Chap 8)

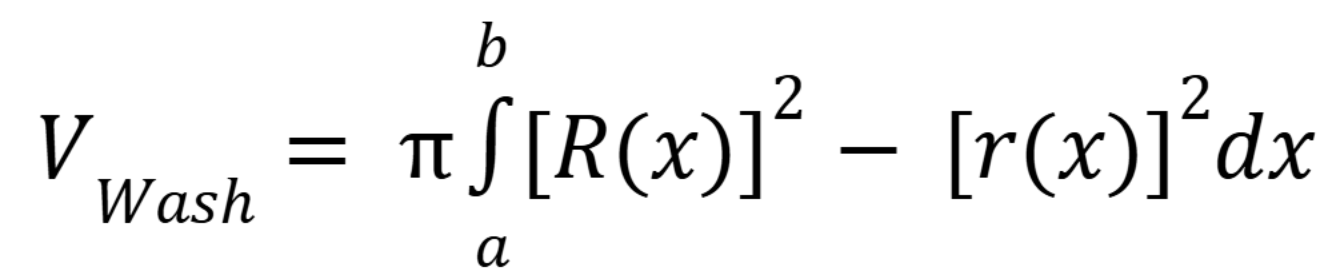
Geometric test

If the series is in the form r^n where r is a constant, and -1 < r < 1 then the series converges. If not, the series diverges (Chap 10)

Justification statement for Geometric test

By the geometric series test, -1 < r < 1, and r=?, therefore this series (Converges or diverges) (Chap 10)

Sum of a geometric series

Sum = a/(1-r). Where a is the starting term and r is the growth factor. (Chap 9/10)

Divergence test

If the limit as n goes to infinity does NOT equal 0, the series diverges. (Chap 10)

Justification statement for Divergence test

(Chap 10)

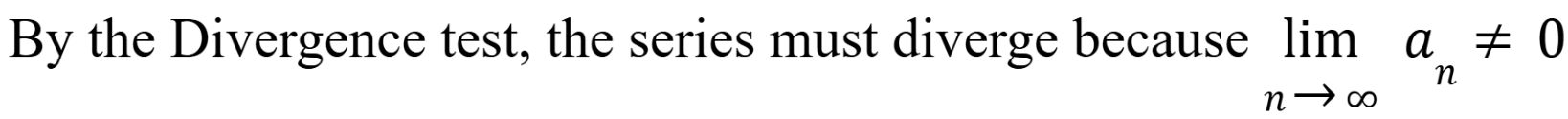
Alternating Series test

If the series is alternating (Positive to negative and etc), If the limit as n goes to infinity of the absolute value of the series equals 0, then the series converges. If the limit isn't 0, then the series diverges. If it equals infinity it diverges (Chap 10)

Justification statement for Alternating Series test

(Chap 10)

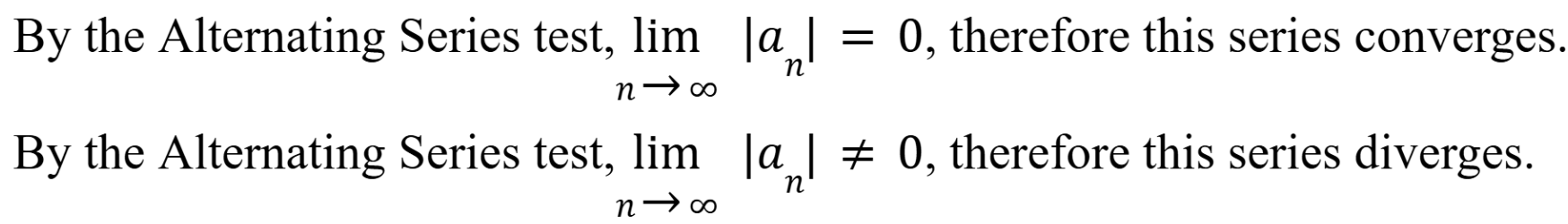
Integral test

If f is a, positive, continuous and decreasing function, on the interval [1,infinity), and the integral from 1 to infinity of the series is finite, then the series converges. You MUST state the function is positive, continuous and decreasing on the interval. (Chap 10)

Justification statement for the Integral test

On the interval [k,infinity). Note: k is the lower bound of the sigma notation. (Chap 10)

P-series test

In the form a/(n^p) where a is a constant. If p is greater than 1, the series converges, if p is less than or equal to 1, the series diverges. No work is necessary for the justification. (Chap 10)

Justification for the P-series test

(Chap 10)

Direct Comparison Test

MUST list first 4 terms of the series. The rule of the thumb is to compare the series to (1/n), or (1/n^2). You need to determine if the series your comparing it too is converging or diverging, and use that to determine if the original series converges or diverges. (Chap 10)

Justification for the Direct Comparison test

Use another test and compare. (Chap 10)

Limit comparison test

If the direct comparison test does not work, then you will usually use a limit comparison test. You need to compare the series to another expression.. If the limit as n goes to infinity of their ratios is finite and NOT 0, then both series must converge, or both diverge (Chap 10)

Justification for limit comparison test

Ratio test

If it equals 1, its inconclusive (Chap 10)

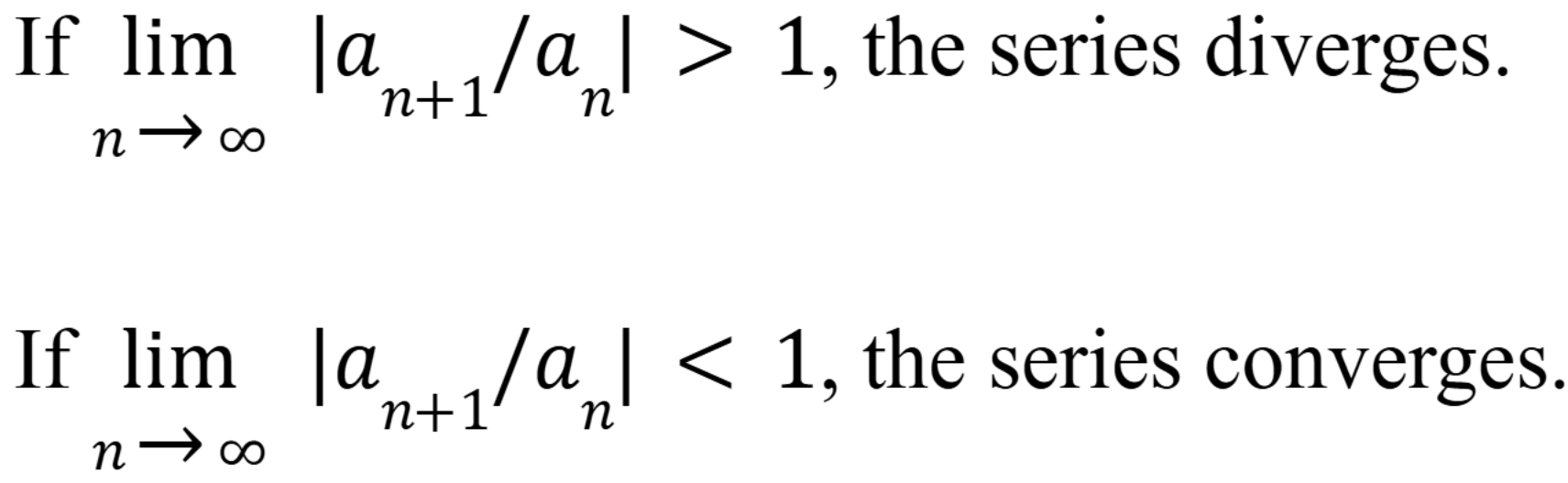
Justification for Ratio test

(Chap 10)

Formula for area of a polar function

(Chap 11)

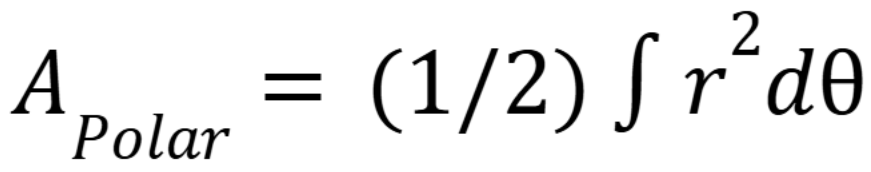
Slope of a parametric

(Chap 11)

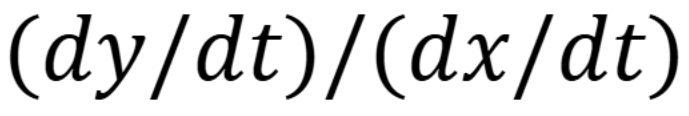
Arc length of parametric

Make sure to include proper unit (Chap 11)

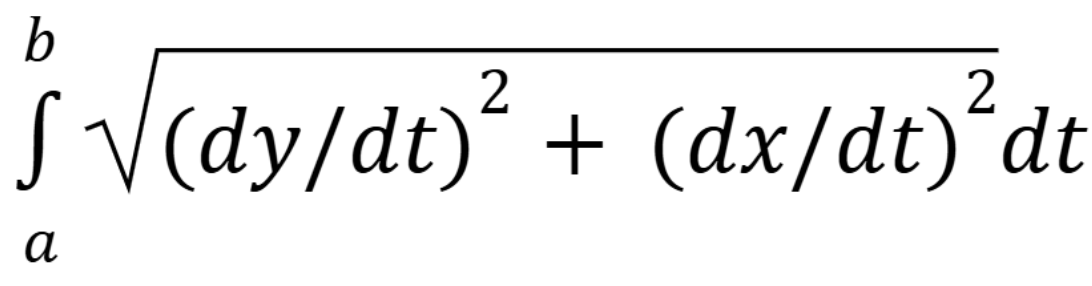
Second derivative of a parametric

(Chap 11)

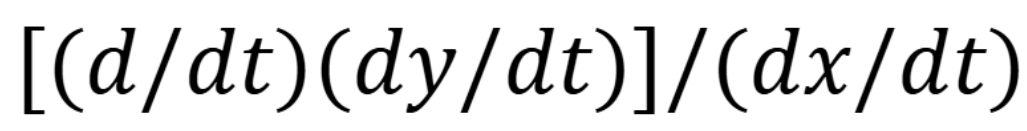
General case for a taylor polynomial around x = a

(Chap 12)

General case for the Maclaurin series for sinx

(Chap 12)

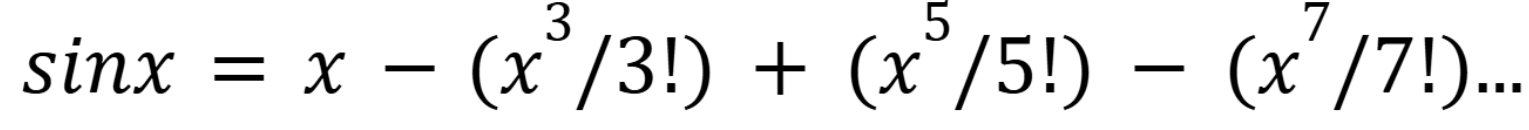
General case for the Maclaurin series for cosx

(Chap 12)

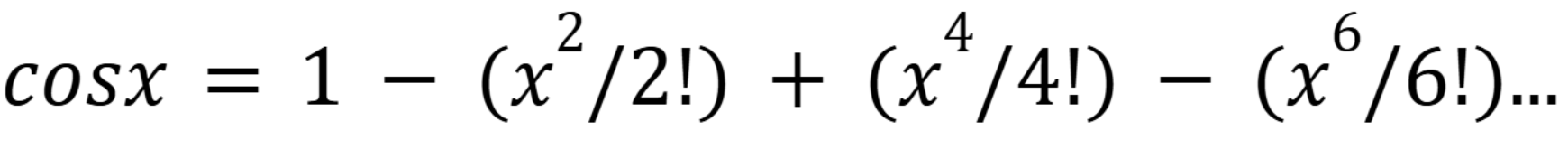
General case for the Maclaurin series for e^x

(Chap 12)

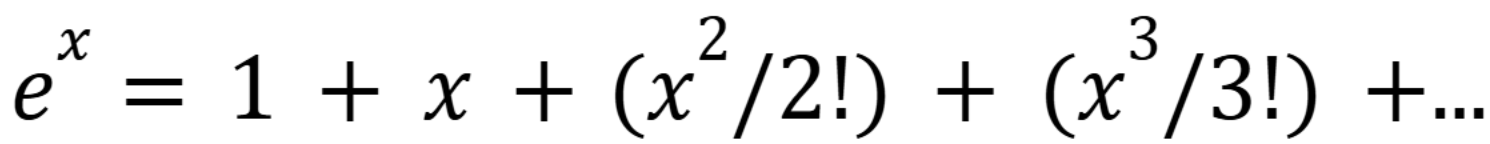
Alternating series error bound formula

(Chap 12)

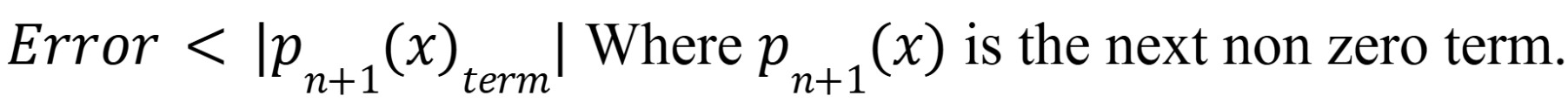
LaGrange Error Formula

(Chap 12)

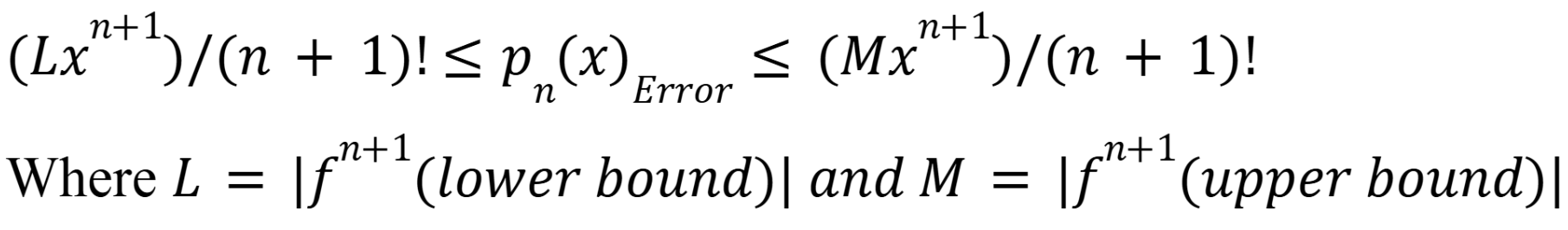
Absolute convergence

If both series, the original series and its non-alternating counterpart converge, then the original series converges absolutely (Chap 12)

Conditional convergence

If the original series, but not the non-alternating counterpart converge, then the original series converges conditionally (Chap 12)