MCAT General Chemistry8: The Gas Phase

1 atm =

~ 760 mmHg ≡ 760 torr = 101.325 kPa

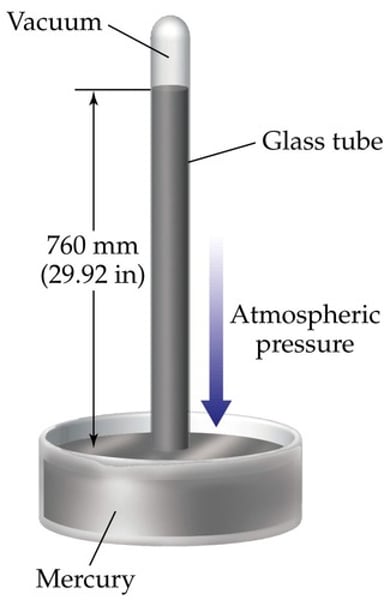
Barometer

~ Atmospheric pressure creates a downward force on the pool of mercury at the base of the barometer while the mercury in the column exerts an opposing force (its weight) based on its density.

The weight of the mercury creates a vacuum in the top of the tube. When the external air exerts a higher force than the weight of the mercury in the column, the column rises.

When the external air exerts a lower force than the weight of the mercury, the column falls. Thus, a reading can be obtained by measuring the height of the mercury column (in mm), which will be directly proportional to the atmospheric pressure being applied

Ideal Gas

~ A hypothetical gas with molecules that have no intermolecular forces and occupy no volume

~ Many compressed gases are very close

-When n, R, and T are held constant, one can easily analyze the

relationship between pressure and volume

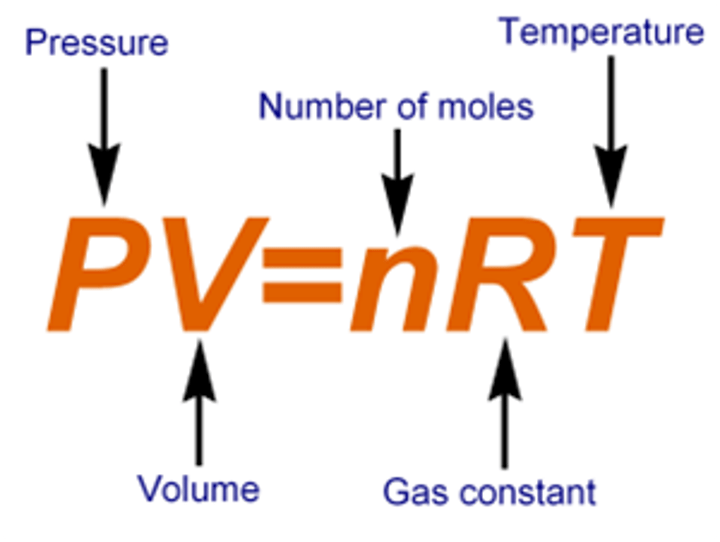
Ideal Gas Law (R) and eq

~ R = 8.21 x 10 ^-2 Latm /mol Kor 8.314 J/ mol K

Density ( how do can you calculate in a gas)

= PM/RT

ratio of mass per unit volume

What volume would 12 g of helium occupy at 27°C and a

pressure of 380 mmHg?

Combined Gas Law

It can be used to relate

changes in temperature, volume, and pressure of a gas:

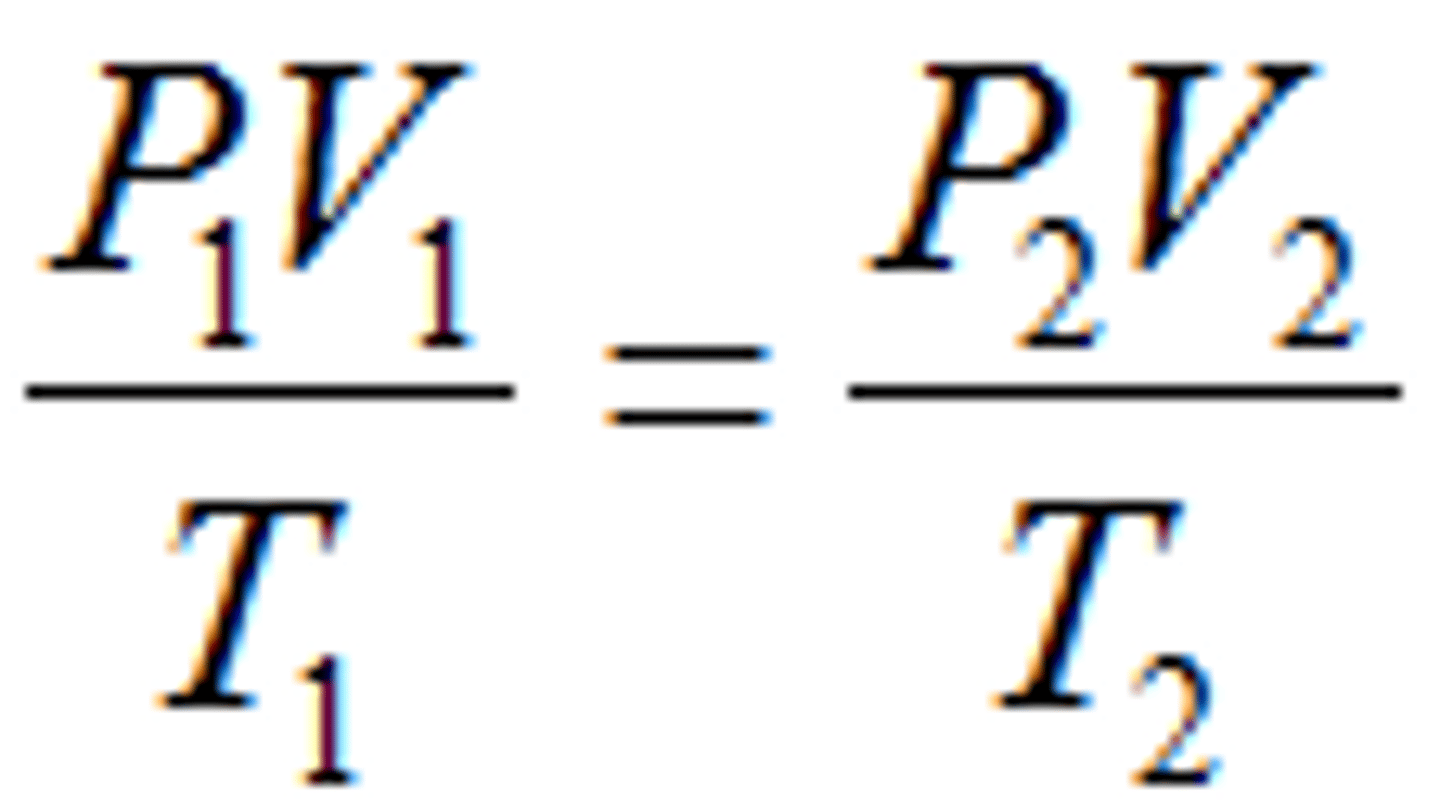
What is the density of CO2 gas at 2 atm and 273°C?

What is the molar mass of a 22.4 L sample of gas that has

a mass of 336 g at a temperature of 546°C and a pressure of 10 atm?

Molar Mass of gas (how do you find it)

= Pstp x 22.4

The molar mass can then be calculated as the product

of the gas's density at STP and the STP volume of one mole of gas

Avogadro's Principle

~ States that all gases at a constant temperature and pressure occupy volumes that are directly proportional to the number of moles of gas present

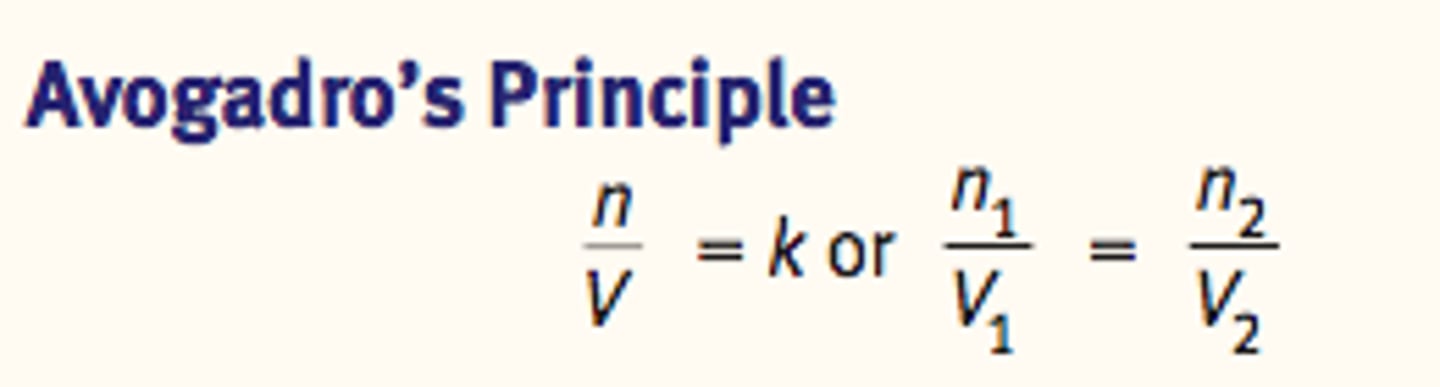
Boyle's Law

~ Given gaseous sample held at constant temperature (isothermal conditions), the volume of the gas is inversely proportional to its pressure

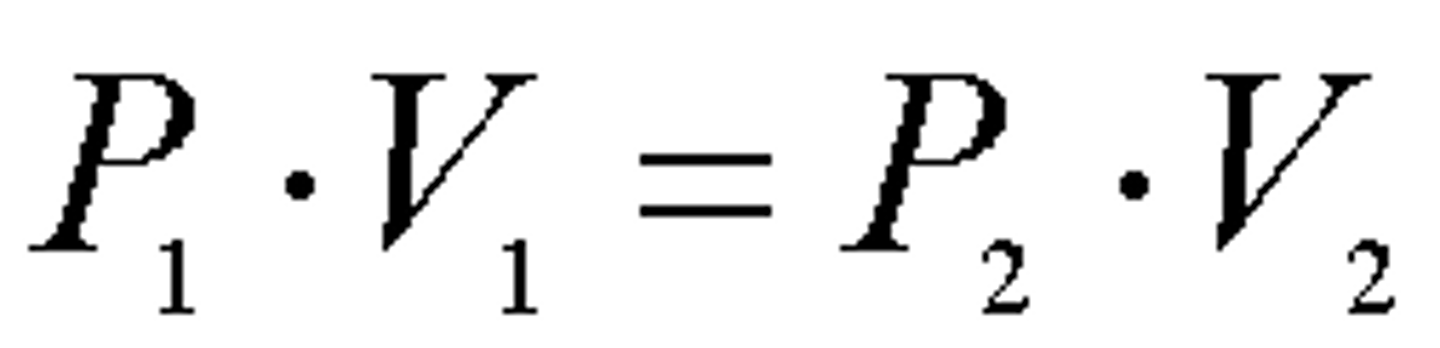
Charles's Law

~ Constant pressure, the volume of a gas is proportional to its absolute temperature, expressed in kelvin (isobaric expansion)

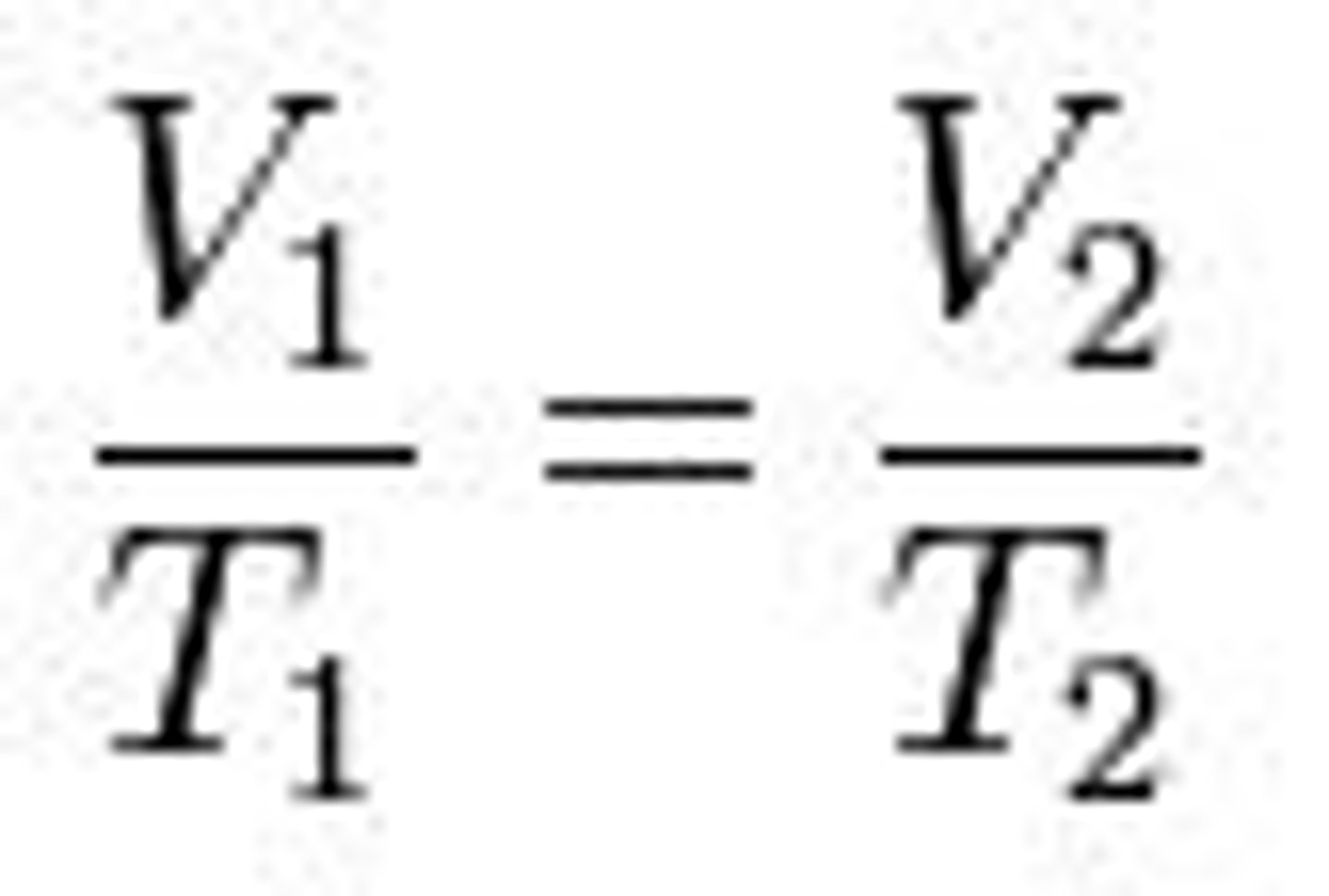
Guy-Lussac's Law

~ An increase in temperature will increase the pressure in direct proportion (isovolumetric)

Dalton's Law of Partial Pressures

~ Total pressure of a gaseous mixture is equal to the sum of the partial pressures of the individual components

When more than one gas is in a

container, each contributes to the

whole as if it were the only gas present.

Add up all of the pressures of the

individual gases and you get the whole

pressure of the system.

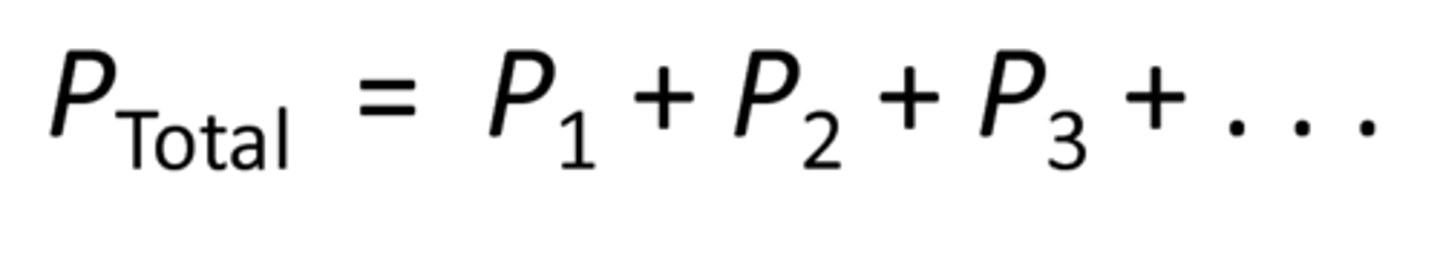
Partial Pressure

The partial pressure of a gas is related to its mole fraction and can be determined

using the following equation:

where Xa moles of gas A/total moles of gas

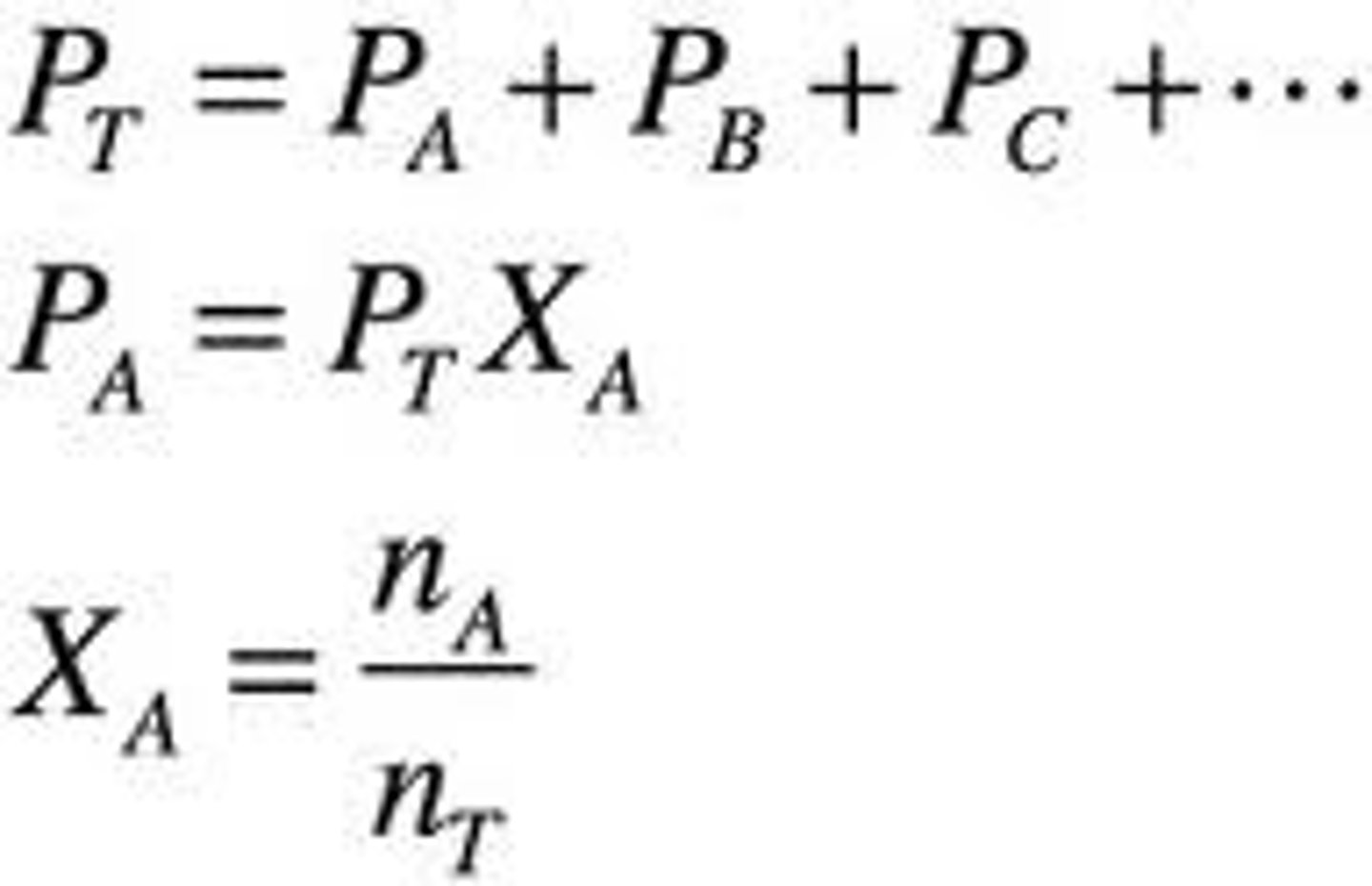
Henry's Law

Vapor pressure from the evaporated molecules forces some of the gas back into

the liquid phase, and equilibrium is reached between evaporation and condensation.

at various applied pressures, the concentration

of a gas in a liquid increased or decreased.

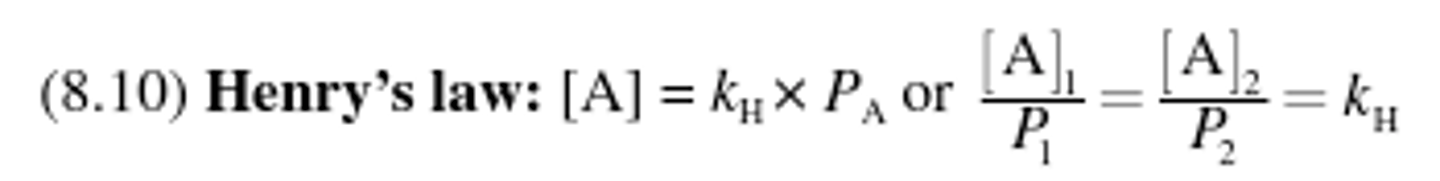
Vapor Pressure

~ Pressure exerted by evaporated particles above the surface of a liquid

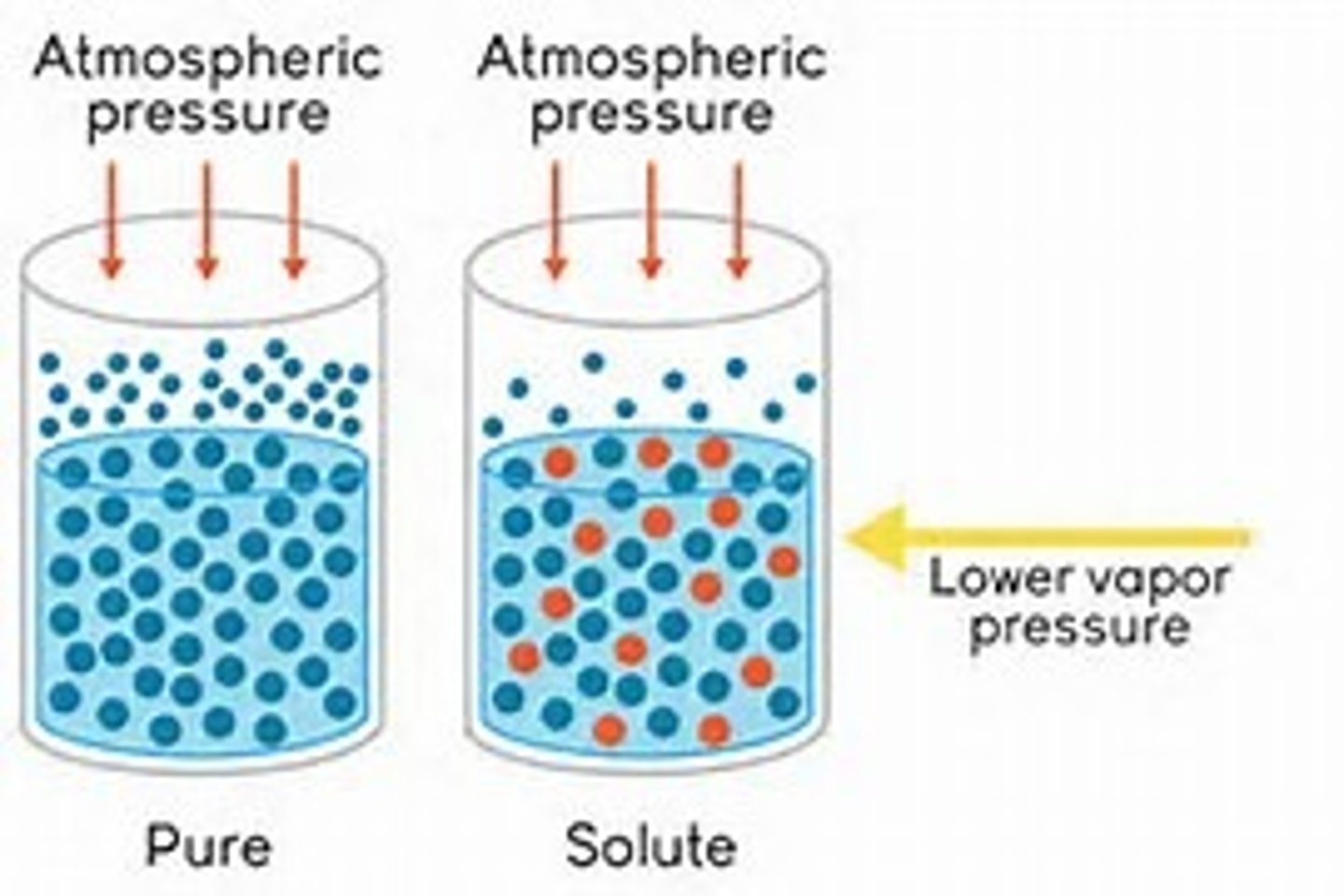
The solubility of a gas will increase with

increasing partial pressure of the gas.

Average Molecular Speeds of a gas particle

the average kinetic energy of

a gas particle is proportional to the absolute temperature of the gas:

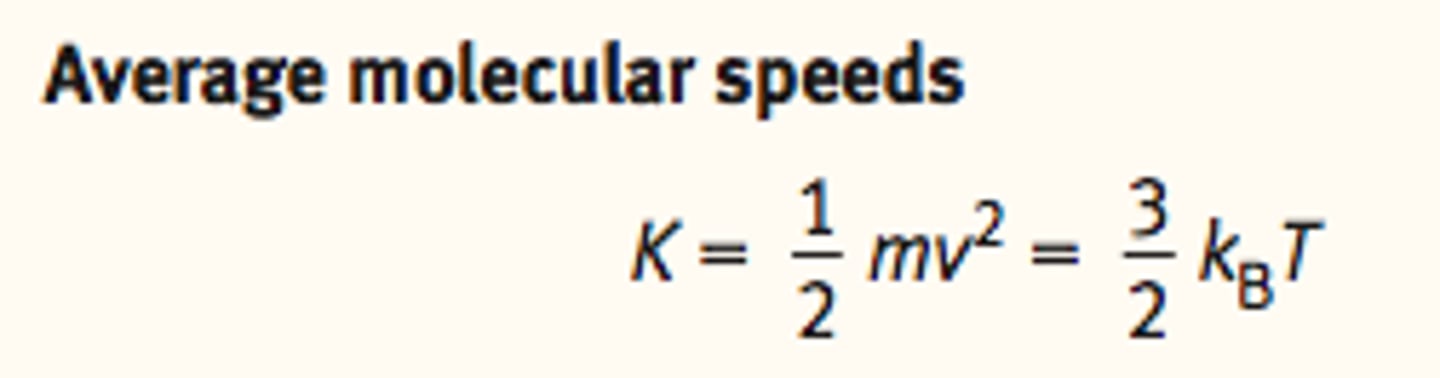
Boltzmann Constant

~ Serves as a bridge between the macroscopic and microscopic behaviors of gases

behavior of the gas as a whole and the individual gas molecules

speed of a gas particle is related to its absolute temperature.

However, because of the large number of rapidly and randomly moving gas particles,

which may travel only nanometers before colliding with another particle or the container

wall, the speed of an individual gas molecule is nearly impossible to define.

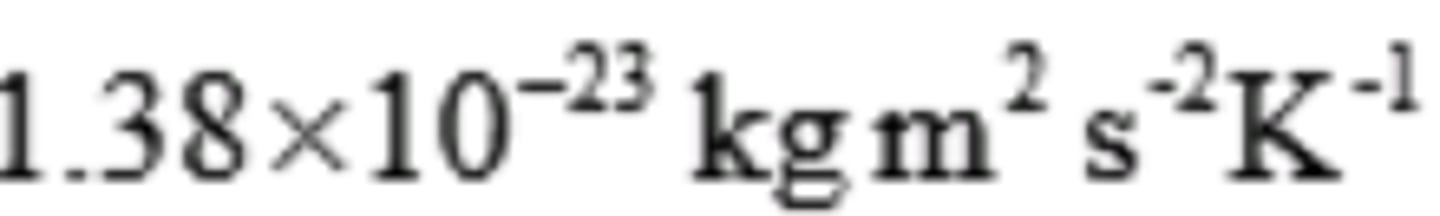
Root-Mean-Square Speed

define an average speed is to determine the average kinetic energy per

particle and then calculate the speed to which this corresponds

R is the ideal gas constant, T is the temperature, and M is the molar mass

Maxwell-Boltzmann Distribution Curve

higher the temperature, the faster

the molecules move. The larger the

molecules, they slower they move.

The more massive the gas particles, the slower their average speed.

Graham's Law

Diffusion and effusion of gases

low molar mass = diffuse/effuse FASTER

higher molar mass = diffuse/effuse SLOWER

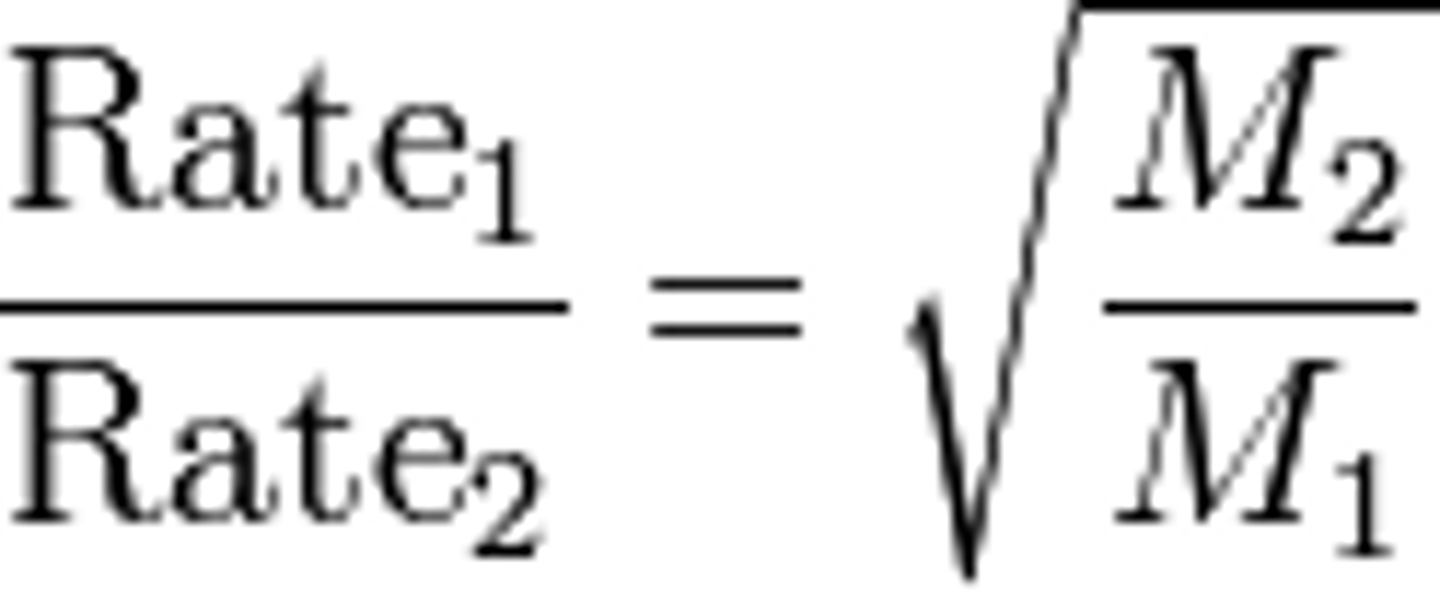
Diffusion vs Effusion

Diffusion—When gases mix with one

another.

Effusion—When a gas moves through a

small hole under pressure.

Both will be slower for larger molecules.

Both conditions use the same equation.

Real Gas and Pressure

~ Ideal would compress to 0 volume

At high temperature and low pressure

(high volume), deviations from ideality

are usually small; good approximations

can still be made from the ideal gas law.

Van Der Waals Equation of State

~ Correct for deviations of real gases

a is the van der Waals term for the

attractive forces.

b is the van der Waals term for big

particles. (if a and b are both zero - use ideal gas law)