Machine Learning Review Questions Week 8

What is imbalanced classification?

Data imbalance usually reflects an unequal distribution of classes within a dataset. For example, in a credit card fraud detection dataset, most transactions are not fraudulent, and very few instances are fraudulent.

Logistic regression (LR) is a multi-class classifier. (True or False?)

False. This algorithm has extensions for multi-class, but logistic regression is a two-class classifier.

What is the role of logit (i.e., 𝑓(𝚾) = 𝑤₀ + 𝑤₁𝑥₁ + ⋯ + 𝑤ᵣ𝑥ᵣ) in logistic

regression?

Logistic regression is a linear classifier, and logit is a linear function applied to a data point's attributes. Variables 𝑤₀, 𝑤₁ ⋯ 𝑤ᵣ are learned coefficients of the model. Initially, all parameters are randomly set. Then, log loss is calculated by using all data points. The derivative of log loss with respect to 𝑤_i is calculated. Using gradient descent, the value of 𝑤_i will be updated.

What is the logistic function applied to 𝑓(𝚾)?

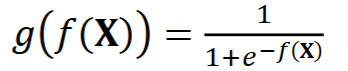
How does logit classify the data?

Features of the data,𝑥₁ + ⋯ + 𝑥ᵣ are plugged into 𝑓(𝚾) If the result is positive, the label is “1;” otherwise, it is “0.”

Why do we apply the logistic function to the 𝑓(𝚾)?

The logistic function converts the results of the logit to probability values between zero and one.

Consider the following model for logistic regression: 𝑃 (𝑦 = 1|𝑥, 𝑤) = 𝑔(𝑤଴ + 𝑤ଵ𝑥), where g(z) is the logistic function. In this equation, what would be the range of P?

P is a probability value between 0 and 1. 0 ≤ 𝑃 ≤ 1

In logistic regression, what are the labels of the data?

Data points have labels “1” and “0”.

In logistic regression, what does the following describe? 𝑃 (𝑦 = 1|𝑥, 𝑤)

It expresses the probability of the label being “1” for a data point with features 𝑥 using the logit function with trained parameters 𝑤.

What is the role of Bernoulli distribution in logistic regression?

During the training phase, we calculate 𝑃 (𝑦 = 1|𝑥, 𝑤) . We calculate this probability using a logistic function: the probability of y being 1. Then, based on Bernoulli distribution and the actual label, we choose either P(y|x) or 1-P(y|x). We use one of these two probabilities to calculate the loss. For example, if the actual label is “0” and 𝑃 (𝑦 = 1|𝑥, 𝑤) is close to zero, the classification has performed well and the loss would be minimal.

During the test, do we use the Bernoulli distribution?

No. We have the logistic function with the correct set of parameters for the test phase. If the output is less than 0.5, the label is “0”; otherwise, it is “1.”

Assume that each data point has two features, 𝑥₁ and 𝑥₂. Also, 𝑓(𝑥) = 𝑤₀ + 𝑤₁𝑥₁ + 𝑤₂𝑥₂ , 𝑤₀ = 5, 𝑤₁ = 0, 𝑎𝑛𝑑 𝑤₂ = −1.

Draw 𝑓(𝑥) on a two-dimensional graph with 𝑥₁ 𝑎𝑛𝑑 𝑥₂ axis. Also, show on the graph which side of 𝑓(𝑥) will be classified as 0, and which side will be labeled 1.

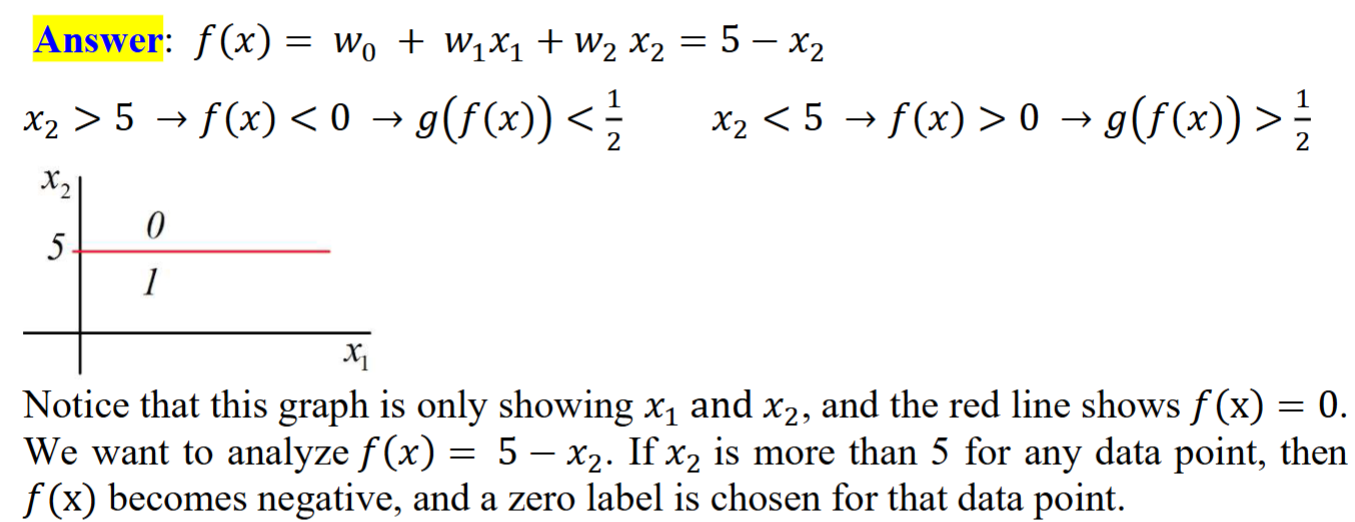
What is the main difference between Naïve Bayes and logistic regression?

Naïve Bayes is a generative model, and logistic regression is a discriminative model.

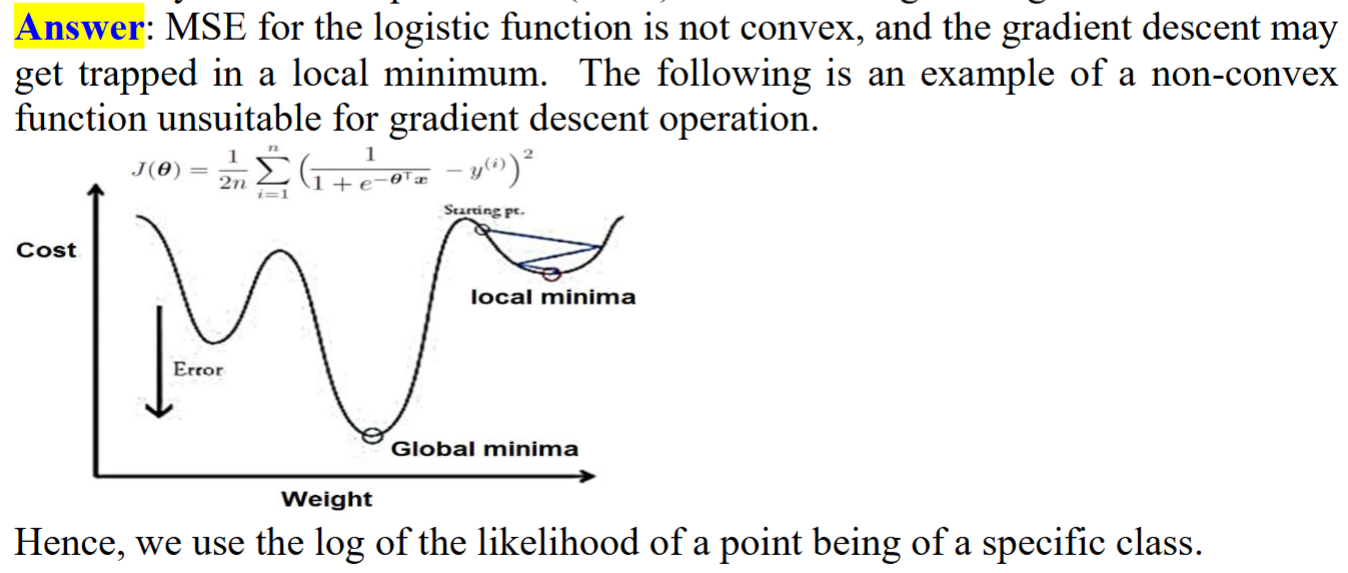
Why is a mean square error (MSE) not used in logistic regression?

How do we calculate the loss in logistic regression?

Cross-entropy is used

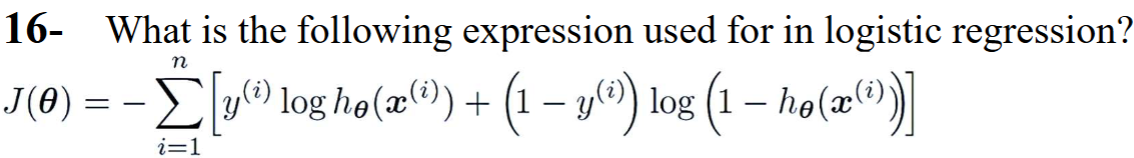
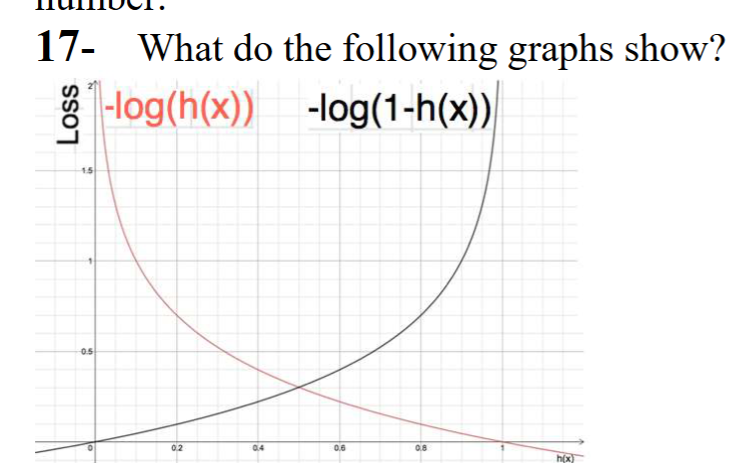
The behavior of the loss function for data points of each class is shown. The loss for any data point with zero label follows the graph on the right. If the probability of that point belonging to the zero label is high (1 − ℎ_\theta(𝑥⁽ⁱ⁾) ≅ 1) the loss becomes zero. The graph on the left shows the loss function for data points with label one.

Logistic regression is used for:

b) Classification tasks (predicting a categorical value)

The output of a logistic regression model is:

b) A probability between 0 and 1

The sigmoid (logistic) function in logistic regression:

b) Transforms the input into a probability between 0 and 1

Which of the following metrics is NOT typically used to evaluate the performance of a logistic regression model?

b) Mean Squared Error

Logistic regression assumes a linear relationship between the features and the target variable.

True

The decision boundary in logistic regression is always linear.

False

Overfitting can occur in logistic regression.

True

Regularization techniques, like L1 or L2 regularization, can be applied to logistic regression.

True

Logistic regression can only be used for binary classification problems (two classes)

False. Explanation: It can be extended to multi-class using techniques like One-vs-Rest

What does the acronym SVM stand for?

Support vector machine.

What is the primary objective of an SVM classifier?

To find the optimal hyperplane that maximally separates different classes in the feature space.

What is a hyperplane in SVM?

A hyperplane is a decision plane that separates objects of different classes.

What is a support vector in SVM?

A data point in a class closest to the hyperplane is called a support vector. Support vectors influence the position and orientation of the hyperplane.

What is a “margin” in SVM?

If the training data is linearly separable, we can select two parallel hyperplanes that separate the two data classes to make the distance between them as large as possible. The region bounded by these two hyperplanes is called the "margin," and the maximum margin hyperplane is the hyperplane that lies halfway between them.

H0 is the hyperplane. H1 and H2 are the planes that touch the support vectors. The distance between H1 and H2 is the margin, the sum of d- and d+.

Why is SVM popular in medical image classification tasks?

SVM performs well with high-dimensional data, common in medical imaging, and can handle small sample sizes effectively.

What is the difference between a hard-margin SVM and a soft-margin SVM?

Hard-margin SVM requires perfectly separable data, while soft-margin SVM allows some misclassifications to handle noisy data.

How can SVM be used for tumor detection in medical images?

By training on labeled tumor and non-tumor regions, SVM can classify pixel or patch-level features to detect tumor areas.

What is the relationship between the magnitude of noise in the data and the size of the margin in SVM?

Increasing noise would result in a reduction of the margin.

What happens in SVM if we do not perform regularization?

The number of coefficients would increase, and overfitting could occur.

What is the consequence of regularization in SVM?

A more considerable margin and a lower chance of overfitting.

When do we expect to have low generalization errors?

A larger margin would result in better test results and lower generalization error. Hence, regularization is performed to avoid overfitting and keep a considerable margin.

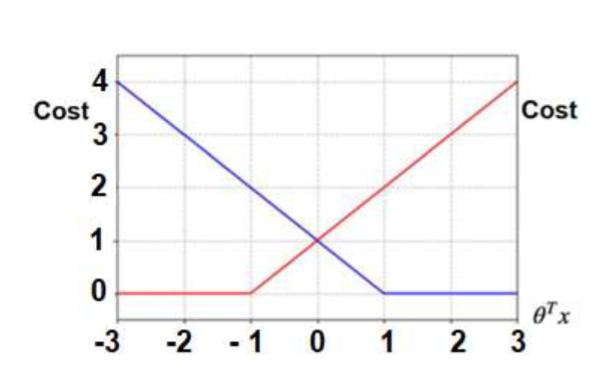
Explain the following curves for the SVM cost function.

The blue curve is for label 1. If 𝜃^T𝑥 becomes negative, then the cost increases proportionally to 𝜃^T𝑥. Hence, for any data point with label one, we want 𝜃^T𝑥 > 0, and 𝜃^T𝑥 < 0 for those of the label 0.

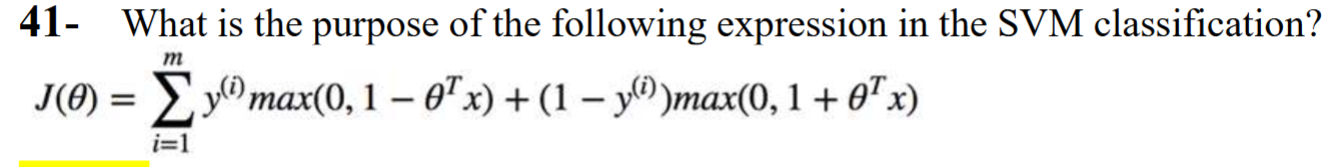
It shows the cost for the total of m data points. Each data point has either an actual label of 𝑦⁽ⁱ⁾ = 1 or 0? The cost for each class 1 data point is 𝑚𝑎𝑥 (0, 1 − 𝜃^T𝑥). For example, if a data point has the label “1” and the hyperplane function 𝜃^T𝑥 returns 20, then the cost would be 𝑚𝑎𝑥 (0, −19) , which is 0.

However, if a data point with label “1” produces -9 during the training, it will result in a cost of 1-(-9)=10, meaning that parameters should be tuned.

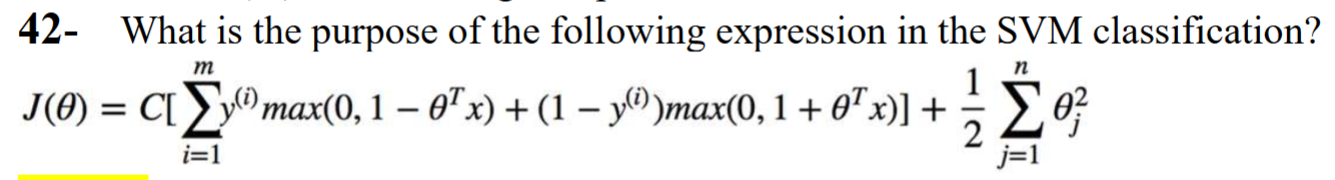
What does the hyperparameter C control in SVM?

C controls the trade-off between maximizing the margin and minimizing classification errors.

What is the role of the size of parameter C in the cost function of SVM?

A larger value of C forces the learning process to reduce the training error as much as possible. A large C would result in a smaller margin and a higher chance of overfitting. Hence, C controls the tradeoff between the model's simplicity and the data's misclassification.

What happens if C in SVM is very small?

Underfitting and high misclassification could occur. In a high-dimensional space, the hyperplane separating the classes becomes overly simplified. The hyperplane may only rely heavily on a few dominant features, ignoring potentially significant information from other features.

What is the kernel trick in SVM?

The kernel trick transforms data into a higher-dimensional space to make it linearly separable without explicitly computing the transformation.

What does a kernel do in SVM classifiers?

In Support Vector Machine (SVM) classifiers, kernels transform the original input data into a higher-dimensional space where the data is more easily separable. The kernel function calculates the similarity between two data points in the original space. The kernel maps them to a new space, where the SVM finds the hyperplane that maximally separates the classes. The kernel function defines this mapping and allows the SVM to perform its classification task without explicitly computing the coordinates of the data points in the higher-dimensional space.

How does SVM handle non-linearly separable data?

SVM uses kernel functions to map the data into a higher-dimensional space where it becomes linearly separable.

Name two common kernel functions used in SVM.

Linear kernel and Radial Basis Function (RBF) kernel.

How do we choose a kernel?

There are different types of kernels, such as linear, polynomial, radial basis function (RBF), and sigmoid. The kernel choice depends on the nature of the data and the classification problem. For example, the linear kernel is suitable for linearly separable data, while the RBF kernel can handle nonlinear data.

What does the RBF kernel do?

It shows the similarity between two points by calculating their Gaussian distance. A hyperplane is then calculated for the calculated distances, and support vectors are selected.

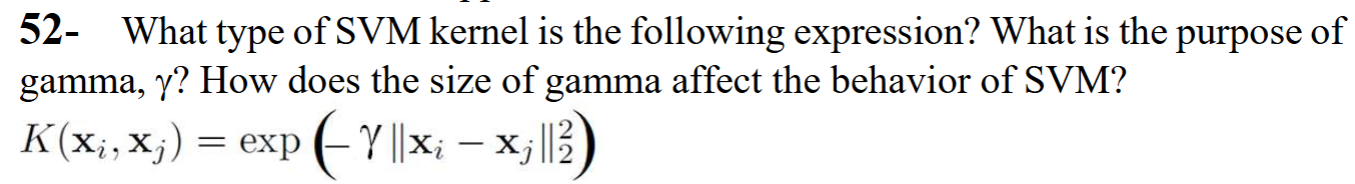
It is an RBF kernel. Gamma is a parameter that controls the effect of the data points on the hyperplane. If Gamma is small, then data points far from the support vectors also influence the shape of the hyperplane.

How do we find the hyperplane of an SVM classifier?

The training data has x features and y labels. We calculate the loss function by initializing \theta values. Then, we use the gradient descent algorithm to find the gradient of the loss function. Finally, we update the parameters using gradients until the process converges.

What is the gradient of the loss function in SVM?

We know that the gradient is the slope of the function. The hinge loss function has a zero gradient for any data point with a “1” label that produces θᵀx ≥ 1. The gradient is -x for these data points if they produce θᵀx < 1. For data points with “0” labels, the gradient of the loss is zero if they produce 𝜃ᵀ𝑥 <= − 1. The gradient of the loss function will be x for such data points if they produce 𝜃ᵀ𝑥 ≥ −1

What is the advantage of using the RBF kernel in medical imaging?

The RBF kernel captures complex, non-linear patterns common in medical images

What is the primary objective of an SVM classifier?

b) Maximize the margin between classes

Which points are referred to as support vectors in an SVM?

b) Points closest to the decision boundary

Which kernel is most used when the data is not linearly separable?

d) Radial Basis Function (RBF) kernel

What role does the parameter C play in an SVM?

c) Balances the trade-off between maximizing the margin and minimizing classification error

In the RBF kernel, what does the parameter γ control?

b) The influence of each training example

True or False: An SVM always uses all data points to define the decision boundary.

False (Only support vectors define the boundary)

True or False: The kernel trick allows SVM to operate in a higher-dimensional space without explicitly transforming the data.

True

True or False: A soft-margin SVM allows some misclassifications to maximize the margin.

True

True or False: Increasing the value of C results in a more flexible decision boundary.

False (A more extensive C results in a stricter boundary with fewer misclassifications)

True or False: The RBF kernel requires pre-selecting support vectors as centers before training.

False (Support vectors are determined during training, not pre-selected)

Why is feature extraction essential before using SVM in medical imaging?

We cannot use the images directly because of their high dimensions.

Extracted features (e.g., texture, intensity, shape) reduce dimensionality and provide more informative input for the SVM classifier.

How can SVM be integrated with deep learning in medical image analysis?

Deep neural networks can extract high-level features, which are then classified using SVM for better generalization.

Why is cross-validation essential when using SVM for medical image classification?

Cross-validation ensures that the SVM generalizes well to unseen data and prevents overfitting.

What is structured data?

Structured data elements can readily be labeled, queried, and analyzed. Examples of structured data elements include age, height, price, numeric data, currency, alphabetic data, names, dates, and addresses.

What is unstructured data?

Qualitative data that cannot easily be classified and queried is unstructured. Examples of unstructured data include images, videos, webpages, PDF files, PowerPoint presentations, emails, blog entries, and word-processing documents.

Considering structured and unstructured data, which type is more suitable for neural networks, and which type for traditional ML methods?

Neural networks are more suitable for unstructured data, such as images, audio, and text, because they can automatically learn complex patterns and representations without requiring extensive feature engineering. In contrast, traditional machine learning methods, such as decision trees and support vector machines, are better suited for structured data, like tabular datasets, where we can use statistical relationships for feature extraction and manual preprocessing

What are the similarities between artificial neurons and human neurons?

Both artificial and human neurons receive inputs, process them based on assigned weights, and produce an output signal if the combined input surpasses a certain threshold. This process essentially mimics a biological neuron's "fire" response. They also share the concept of interconnected networks where information flows through multiple layers of nodes, allowing complex pattern recognition and learning through adjusting connection strengths (weights) based on feedback.

What are dendrites and axons as parts of neuron cells?

Dendrites bring information to neurons, and axons send out information.

What are the three primary components of an artificial neuron?

Weights, bias, and activation function.

What is the role of the weights in an artificial neuron?

They determine the strength of the connection between inputs and the neuron

What does the bias term contribute to the neuron's output?

It allows the neuron to activate even when all inputs are zero, shifting the activation threshold.

What is the purpose of the activation function?

It introduces non-linearity and determines the neuron's output based on the weighted sum of inputs and the bias.

How are the inputs and weights combined before applying the activation function?

They are multiplied and summed (dot product), and the bias is added to the result.

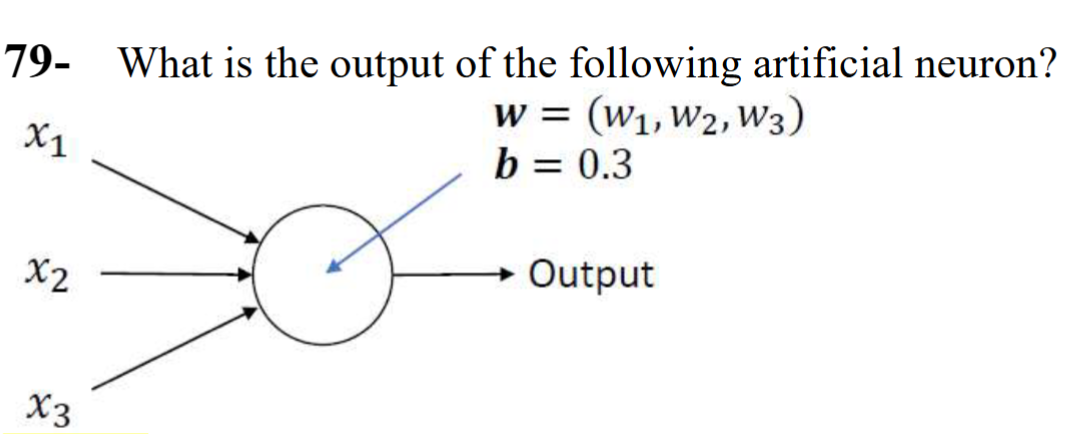
𝑂𝑢𝑡𝑝𝑢𝑡 = 𝑓(𝑥1𝑤1 + 𝑥2𝑤2 + 𝑥3𝑤3 + 𝑏) where 𝑓() is the activation function.

Why are activation functions necessary in neural networks?

They introduce non-linearity, enabling neural networks to learn complex patterns.

What is the primary difference between a linear and a non-linear activation function?

A linear activation function produces a linear output, while a non-linear function produces a non-linear output.

What is the "vanishing gradient" problem, and which activation function is known to help mitigate it?

The vanishing gradient problem is when gradients become very small during backpropagation, hindering learning. ReLU (Rectified Linear Unit) is known to help mitigate this.

In what type of neural network layer is the Softmax activation function typically used?

The output layer of multi-class classification neural networks.

What is the purpose of the Sigmoid activation function, and what range of values does it produce?

The sigmoid activation function produces a value between 0 and 1 and is often used for binary classification.

What is a binary-step activation function?

It compares ∑(𝑥௜𝑤௜) + 𝑏 with a threshold. If the input is above the threshold, the output will be 1; otherwise, the output will be zero.

What types of layers are in an MLP?

Input, hidden, and output.

What is an “input function” in an MLP layer?

The operation performed on that layer's inputs, weights, and bias. Usually, the function is a dot product of the layer's input by the weight vector. Then, the bias is added to the result of the dot product.

What is the mathematical definition of the ReLU activation function?

ReLU (Rectified Linear Unit) is defined as f(x) = max(0, x). If the input (x) is positive, the output is the input itself. If the input is negative, the output is zero.

Why is ReLU considered computationally efficient?

ReLU's computation involves a simple comparison and either outputting the input or zero.

This simplicity avoids complex mathematical operations like exponentials, which are present in sigmoid and tanh functions, making it faster.