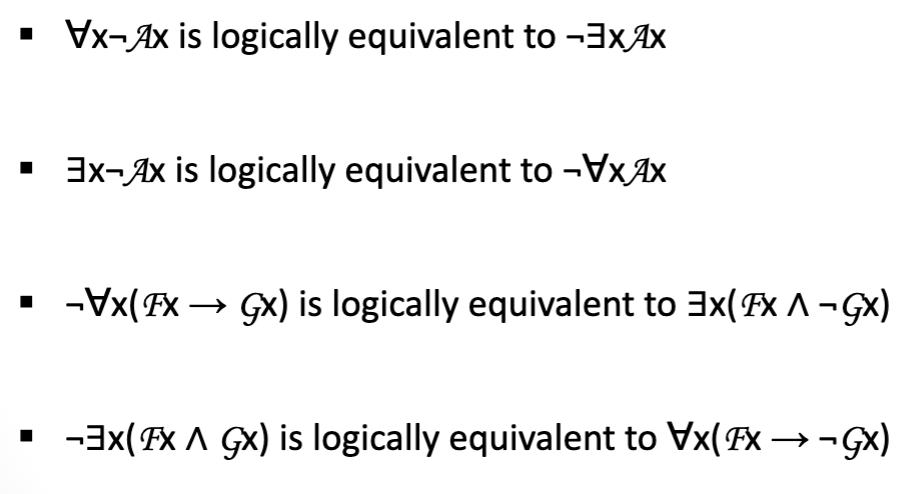First Order Logic

∧ ∨ ¬ ∃x ∀x

Symbolize: Someone is a spy

∃xSx

Symbolize: Everyone is a vegetarian

∀xVx

Symbolize: Every spy is a vegetarian

∀x(Sx → Vx)

Symbolize: Some spy is a vegetarian

∃x(Sx ∧ Vx)

Symbolize: Not every spy is a vegetarian

¬∀x(Sx → Vx) OR ∃x(Sx ∧ ¬Vx)

Symbolize: No spys are vegetarian

¬∃x(Vx ∧ Sx) OR ∀x(Sx → ¬Vx)

What quantifier symbolizes: There is

∃x

What do you do when you have: Only F is G

FLIP ORDER

only dogs like samurai movies: ∀x(Sx → Dx)

What can you say about: ∃x

At least one thing in the domain can be plugged in for x

What can you say about: ∀x

Everything satisfies some condition

Symbolize: hofthor loves somebody

∃xLhx

Symbolize: sombody loves hofthor

∃xLxh

Symbolize: sombody loves themselves

∃xLxx

Symbolize: everybody loves somebody

1. For each person, there’s someone that they love: ∀x∃yLxy

2. There is somebody everyone loves: ∃y∀xLxy

Symbolize: At least one spy

∃xSx

Symbolize: At least two spies

∃x∃y(Sx ∧ Sy ∧ ¬x=y)

Symbolize: At least three spies

∃x∃y∃z(Sx ∧ Sy ∧ Sz ∧ ¬x=y ∧ ¬y=z ∧ ¬x=z )

Symbolize: At most one spy

It’s not the case that there are 2 spies: ¬∃x∃y(Sx ∧ Sy ∧ ¬x=y)

OR

∀x∀y((Sx ∧ Sy) → x=y)

Symbolize: Exactly one spy

∃x(Sx ∧ ∀y(Sy → x=y))

Symbolize: Exactly two spies

There are at least two different spies, and every spy is one of those two

∃x∃y(Sx ∧ Sy ∧ ¬(x = y) ∧ ∀z(Sz → x=y ∨ y = z))

What can you say about: At least

sets min, Quantifier # = n

What can you say about: At most

sets max, Quantifer # = n+1

Symbolize: The

∃x(Fx ∧ ∀y(Fy → x=y) ∧ Gx)

• There is at least one F: ∃xFx

• There is at most one F: ∀y(Fy → x=y)

• and that thing is G: Gx

*symbolizes definite descriptions

Symbolize: The wrestler

∃x(Wx ∧ Ɐy(Wy → x = y))

• there is at least one thing that’s a wrestler and at most one thing that’s a wrestler

Symbolize: Every F is G

∀x(Fx → Gx)

‘Every dog is both in the house and a Jack Russell’: Ɐx(Hx → Jx)

Symbolize: Some F is G

∃x(Fx ∧ Gx)

‘Some dog in the house is a Jack Russell Terrier’: ∃x(Hx ∧ Jx)

• ‘There is some dog that is both in the house and a Jack Russell’

Symbolize: Not all Fs are G

¬Ɐx(Fx → Gx) OR ∃x(Fx ∧ ¬Gx)

‘Not all the dogs in the house are Jack Russell Terriers’:

• ‘It is not the case that every dog in the house is a Jack Russell’: ¬Ɐx(Hx → Jx)

OR

• ‘There is a dog in the house that is not a Jack Russell’: ∃x(Hx ∧ ¬Jx)

Symbolize: No Fs are G

¬∃x(Fx ∧ Gx) OR Ɐx(Fx → ¬ Gx)

‘No dogs in the house are Jack Russell Terriers’:

• ‘It is not the case that there is some dog in the house that is a Jack Russell’: ¬∃x(Hx ∧ Jx)

OR

• ‘Every dog in the house is a non-Jack Russell’: Ɐx(Hx → ¬ Jx)

Some important logical equivalences