linear test 1

rank of a matrix

The rank of a matrix equals the number of nonzero rows in its ROW ECELON FROM

trivial solution

the solution x=0 of a homogeneous equation Ax=0 (when the variables of a homogeneous equation/ matrix are equal to zero)

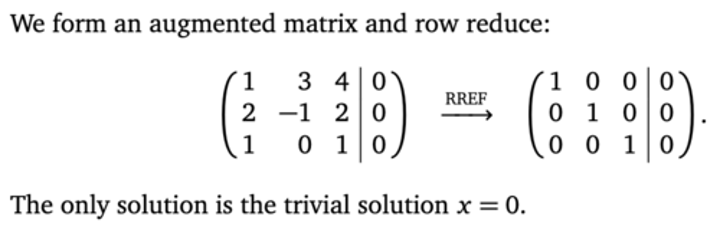
homogenous systems

system where the constant term in each equation is zero (all solutions in the aug. matrix equal zero) if [A | 0 ] is the augmented matrix of a homogenous system & the system has more variables than equations, the system has infinitely many solutions

linearly dependent

Any collection of vectors containing the zero vector must be linearly dependent.

linearly independent

The vectors are not scalar multiples of each other.

empty set AKA an inconsistent system

a set with no solution

consistent system

A system of equations that has exactly one solution or an infinite # of solutions

invertible

a matrix that has an inverse

u and v are orthogonal. FIND || u + v|| ^2

uu+2uv+vv

Transpose of a Matrix

Switch the rows and columns - imagine it kinda swinging up/down a 90 degree angle

diagonal matrix

a square matrix whose entries not on the main diagonal are all zero

identity matrix

1 0

0 -1

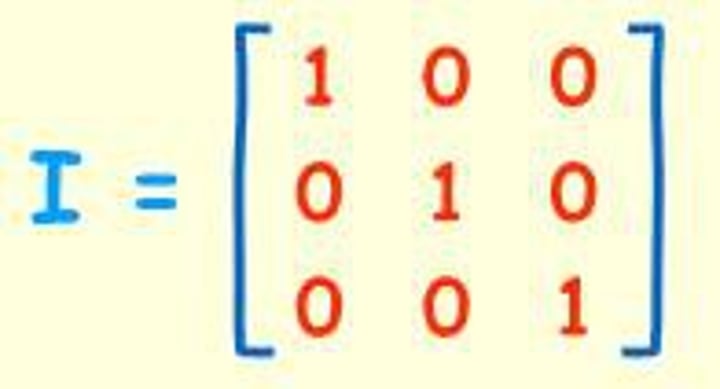
Free variables

Variables that are not governed by any quantifier (basically any column that doesn't have the leading entries in it see photos) (when writing the free variable in vector form, be sure to set it equal to t like x^3 = t)

rank of a matrix

number of nonzero in its ROW ECHELON FORM (if sys. is consistent, then the # of free variables equals -5x^2

gaussian elimination

1. Write augmented matrix of system of linear equations

2. Use elementary row operations to reduce augmented matrix to row echelon form.

3. rewrite equations using the REF form THEN Using back substitution, solve equivalent system that corresponds to row reduced matrix.

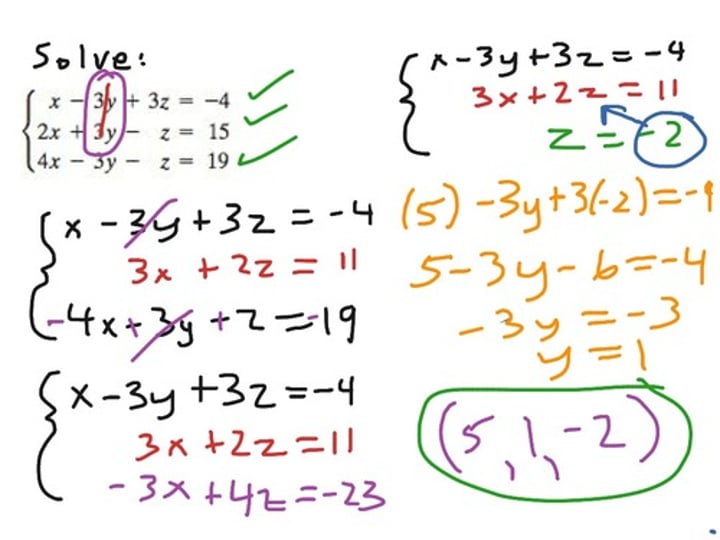
ANY MATRIX WITH MORE COLUMNS THAN ROWS IS LINEAERLY DEPENDENT

ANY MATRIX WITH MORE COLUMNS THAN ROWS IS LINEARLY DEPENDENT!!!

the eigenvalues of any matrix A^-1 are the regular eigenvalues of A just written in the denominator

• Matrix A has eigenvalues 4 & -2 so

• Matrix A^-1 has eigenvalues ¼ and 1/-2 :))