Test 10 circles

diameter

segment that has both endpoints on the circle

radius

segment with one endpoint at the center and the other endpoint on the circle

central angle

an angle whose vertex is at the center of the circle (measure of a central angle is equal to its arc length)

arc

part of a circle, named by its endpoints

adjacent arcs

arcs that have one point in common

arc addition postulate

the measure of the arc formed by two adjacent arcs is the sum of the measures of the two arcs

segment whose endpoints are on the circle

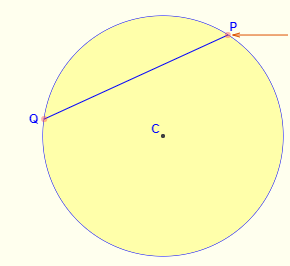
QP is a chord

congruent central angles have congruent arcs

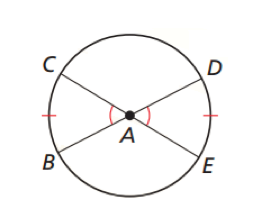
If <BAC is congruent to <EAD then (arc)AB is congruent to CD

congruent central angles have congruent chords

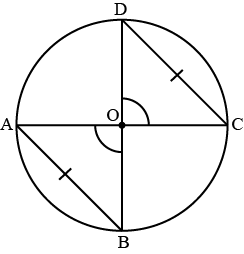
If <AOB is congruent to <COD then (segment) AB is congruent to CD

Congruent chords have congruent arcs

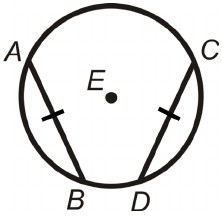
If (segment) AB is congruent to CD then (arc) AB is congruent to CD

chords equidistant from the center are congruent

If (segment) EFis congruent to EG then (segment) AB is congruent to CD

if a diameter is perpendicular to a chord then it bisects the chord and its arc

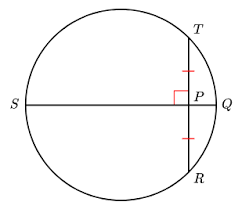
If SQ is the diameter and (segment) SQ is perpendicular to TR then (segment) TP is congruent to PR and (arc) TQ is congruent to QR

If a diameter bisects a chord (that is not the diameter) then it is perpendicular to the chord

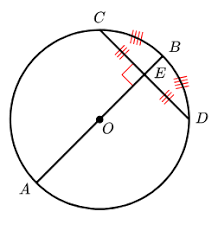
If (segment) AB is the diameter and (segment) CE is perpendicular to ED then (segment) AB is perpendicular to CD

The perpendicular bisector of chord contains the center of the circle

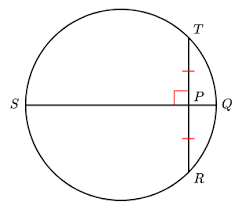
If (segment) QS is the perpendicular bisector of (segment) TR the (segment) QS is the diameter

inscribed angle

an angle whose vertex is on the circle and whose sides are chords

intercepted arc

arc whose endpoints are sides of the inscribed angle

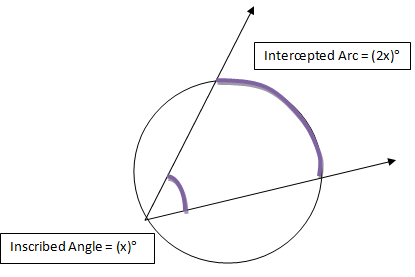
inscribed angle theorem

measure of an inscribed angles is equal to half of its intercepted arc

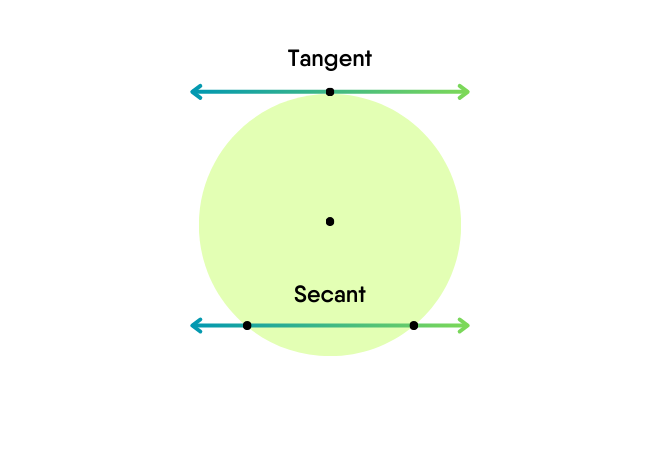
tangent

a line that intersects the circle at only one point outside the circle

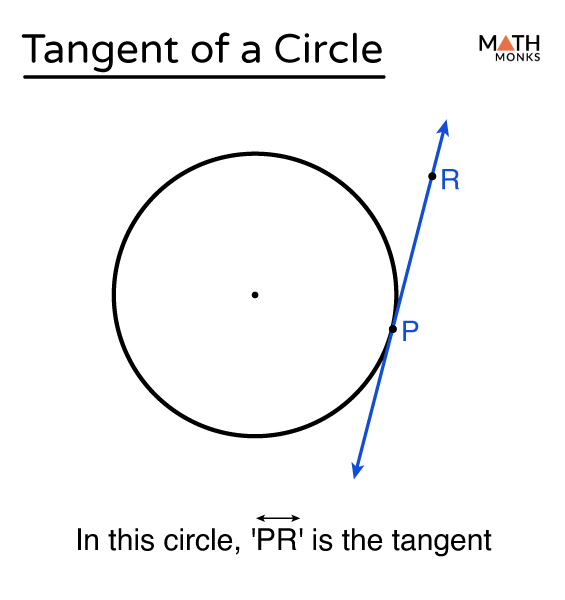
common tangents

line that is tangent to two circles

secant of a circle

a line that intersects the circle at two points

Angle formed by a tangent and a chord

the angle is half its arc

the angle formed by two chords intersecting inside a circle

the angle is ½ the sum of the intercepted arcs

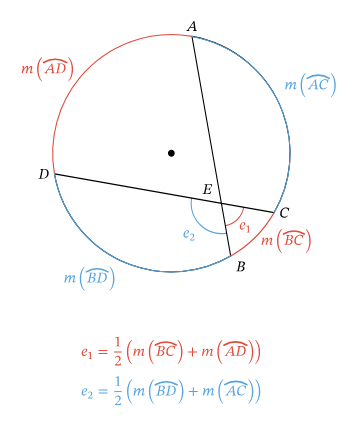
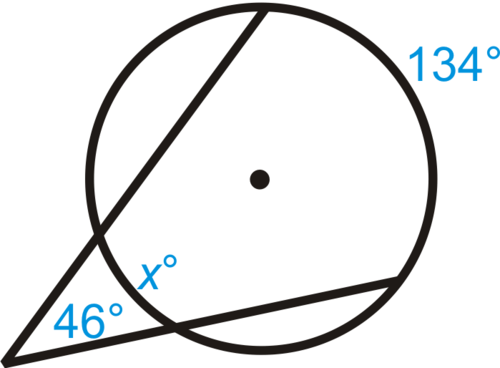
the angle formed by two secants, a tangent and a secant, or two tangents intersecting outside the circle

the angles are ½ the difference of the intercepted arcs7

46 = ½ (134 - x)

46 = 67 - 0.5x

-21 = -0.5x

x = 42

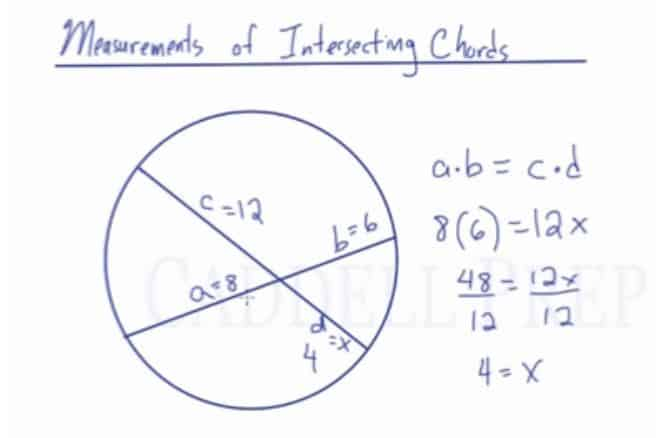
If two chords intersect in a circle,

the product of the segments of one chord equals the product of the segments of the other chord

(a)(b) = (c)(d)

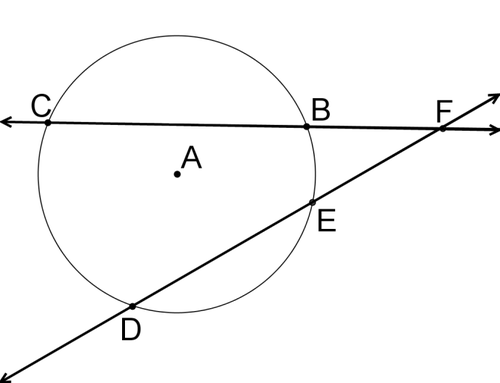
if two secants intersect outside the circle,

then the product of the whole secant and its external segment is equal to the product of the other whole secant and its external segment

(fc)(fb) = (fd)(fe)

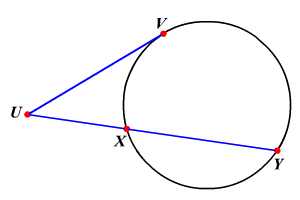
if a tangent and a secant are drawn to a circle from an external point

then the square of the tangent segment is equal to the product of the whole secant and its external segment

(vu)² = (uy)(ux)

equation of a circle if the circle is at the origin

x² + y² = r²

equation of a circle if the circle is not at the origin

(x-h)² + (y-k)² = r²

(h,k)

center

r

radius