Factoring out completely

factoring out completely with common intergers (DO NOT use multiple choice if you want to learn. either use flashcards or written. If you need the symbols copy&paste them from here: https://www.i2symbol.com/symbols/superscript

What is factoring out?

Finding the greatest common factor in a set than multiplying with that number. The opposite of distributive property.

What is the difference between factoring out and factoring out completely?

Factoring out completely means factoring until there are no other numbers that can be factored or until all factors other than monomial factors are prime factors.

What is the key equation in factoring out completely?

a+b=c a⋅b=d. basically the numbers need to add up to the first number and multiply to the second

What does a+b=c a⋅b=d represent?

How to factor for the next step. ex:

9(x²+7-12)

3+4=7 3⋅4=12 or a+b=c a

9(x+3)(x-4)

What does gcf stand for?

Greatest common factor

How do you factor out completely after factoring the first time?

Find 2 numbers that adds up to one number while also multiplying it to the other. Then put those to numbers in parentheses like this:

(x±a) (x±b)

Factor out completely x²+4x

x(x+4)

What do you do if there are no other numbers in an equation to use as the gcf?

You are allowed to use variables when factoring out.

How do you know which variable to use as the gcf when factoring out?

The variable with the lowest exponent is always the gcf

How would you factor when there are only two terms and the term with x² has a number attached (EX: 4ײ-9) ?

You still factor the second term regularly, which is -3 and 3 since they multiply to -9, but you split up the the number when factoring because of distributive property.

4ײ-9 becomes (2x-3)(2x+3).

Why would you use (x+3) (x-3) instead of (x+3) (x+3) or vice versa?

Because a negitive x a postive is a negitive. Therefore you use this method when one of the terms you’re factoring is negitive.

What are you able to factor 5(x²+9) (x²-9) into?

5(x²+9)(x²+3)(x²-3)

*You can do this because the x² is next to the - sign

Factor 12y²-18y⁵

6y²(2-3y³)

Factor 18m²-2 completely

2(3m+1)(3m-1)

Factor 2x²+16x-18 completely

2(x+9)(x-1)

Factor 5x³-80x completely

5x(x+4)(x-4)

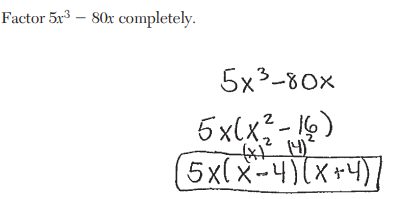
Factor 20x³-45x completely

5x(2x+3)(2x-3)

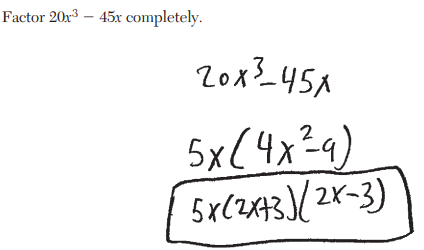
Factor 36-4x² completely

4(x+3)(x-3)

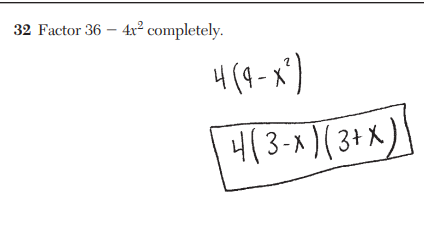
factor out 4x³-49

4x²(x+7)(x-7)

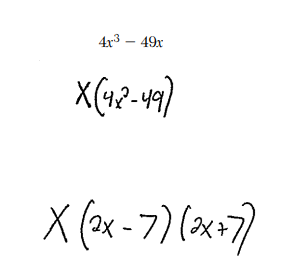
Factor x³-13x²-30x completely

x(x+2)(x-15)

When factoring out a term with an variables or numbers, ____ is removed from other exponents. Most of the time this means ___ is removed from other terms exponents, resulting in any term with that amount of ______ to disappear

the number of the exponent you factored out

1 integer.

exponents.

Factor p⁴-81

(p²+9)(p+3)(p-3)

TIP: When factoring find all numbers that ___ up to the first number and all numbers that ____ to the second number. Look through those selection of numbers.

add, multiply

What do you do if after factoring you have two terms like x(2-3׳) ?

You would stop factoring and leave the equation as is.