functions + quadratics

how to find the vertex

• at²+bt+c

• t = b/2a

• substitute

• e.g t²-3t = y

• a = 1, b = 3

• t = 3/2

• (3/2)² - 3(3/2)

• (9/4) - (9/2)

• = -9/4

how to find range

• insert endpoint of domain into the function

• find the vertex

• compare values, smallest is lowest possible value biggest is highest possible value 

domain vs range

• domain - possible x values

• range - possible y values

quadratic formula

(-b ± square root of bsquared - (4ac))/2a

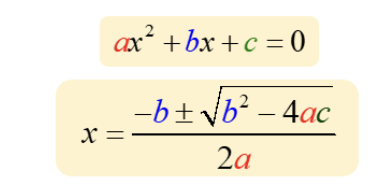
how do you know if 2 functions are inverse

if f(g(x))=x and g(f(x))=x f and g are inverse

domain + range of inverse functions

the domain of a function is the range of it’s inverse and vice versa.

vertex formula

((-b/2a),(c-(b²/4a)))

vertex form

a(x+p)²

how to find if functions are odd or even

• function = f(x)

• to find whether it is odd or even do f(-x)

• if f(-x) = f(x) → even

• if f(-x) = -f(x) → odd

• if f(-x) does not = -f(x) or f(x) → neither

2 functions which are neither odd nor even but their product is even

• f(x) = x-1

• g(x) = x+1

• f(x)g(x) = x²-1

domain restrictions

• denominator cannot = 0

• inside of square root has to be bigger or equal to 0

• inside of log has to be bigger than 0

one to one function

• above x-axis

discriminant

= b²-4ac

discriminant > 0

2 distinct answers/roots/solutions/x-intercepts

descriminant = 0

1 answer/repeated root/solution/x-intercept/equal roots

discriminant < 0

no real solutions

how to know if a function has an inverse or not

• horizontal line test - If a horizontal line intersects two or more points anywhere on the graph, it is not invertible

• in a table - if the same output shows up multiple times for different inputs, the function is not invertible.

equation of a line - point slope form

y-y1 = m(x-x1)