4.2 Unit circle and Values and tricks

UNIT CIRCLE FORMULA

x²+y²=1

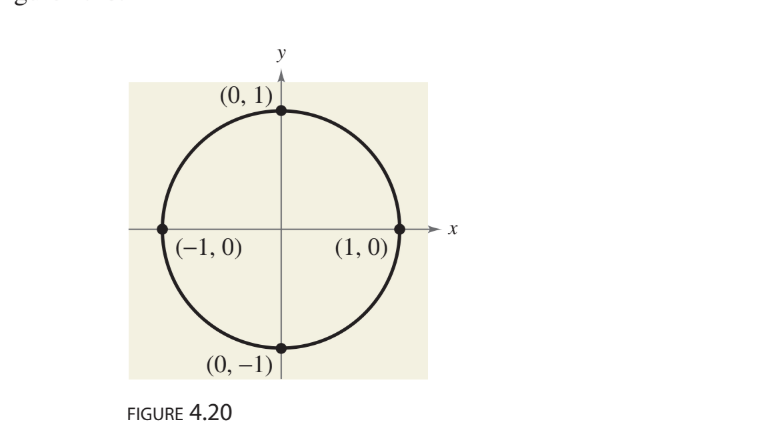
On Unit circle what are Sin and Cos

Sin=y-value

Cos-x-value

ON UNIT CIRCLE WHAT ARE VALUES FOR ALL TRIG FUNCTIONS IN X and Y terms

sinx=y cosx=x tanx=y/x. x cannot equal 0. cotx= x/y. y cannot equal 0. secx= 1/cos. cos cannot be 0. cscx=1/sin. sin cannot be 0

Practice problem: Find 4 values of theta (2 + and 2- ) that satisfy the following equation: cos theta =( -square root 3 /2) Give your answer in radians

5π/6, 7π/6, -5π/6, -7π/6

Practice problem: evaluate the six rtrig functions where sec(theta)=-17/8 and sin theta >0

sin(theta)=15/17

cos(theta)= -8/17

tan(theta)=-15/8)

sec(theta)=-17/8

csc(theta) = 17/15

cot(theta) -8/15

0°

Radians: 0, sin θ: 0, cos θ: 1, tan θ: 0, csc θ: undefined, sec θ: 1, cot θ: undefined

30°

Radians: π/6, sin θ: 1/2, cos θ: √3/2, tan θ: √3/3, csc θ: 2, sec θ: 2√3/3, cot θ: √3

45°

Radians: π/4, sin θ: √2/2, cos θ: √2/2, tan θ: 1, csc θ: √2, sec θ: √2, cot θ: 1

60°

Radians: π/3, sin θ: √3/2, cos θ: 1/2, tan θ: √3, csc θ: 2√3/3, sec θ: 2, cot θ: √3/3

90°

Radians: π/2, sin θ: 1, cos θ: 0, tan θ: undefined, csc θ: 1, sec θ: undefined, cot θ: 0

120°

Radians: 2π/3, sin θ: √3/2, cos θ: -1/2, tan θ: -√3, csc θ: 2√3/3, sec θ: -2, cot θ: -√3/3

135°

Radians: 3π/4, sin θ: √2/2, cos θ: -√2/2, tan θ: -1, csc θ: √2, sec θ: -√2, cot θ: -1

150°

Radians: 5π/6, sin θ: 1/2, cos θ: -√3/2, tan θ: -√3/3, csc θ: 2, sec θ: -2√3/3, cot θ: -√3

180°

Radians: π, sin θ: 0, cos θ: -1, tan θ: 0, csc θ: undefined, sec θ: -1, cot θ: undefined

210°

Radians: 7π/6, sin θ: -1/2, cos θ: -√3/2, tan θ: √3/3, csc θ: -2, sec θ: -2√3/3, cot θ: √3

225°

Radians: 5π/4, sin θ: -√2/2, cos θ: -√2/2, tan θ: 1, csc θ: -√2, sec θ: -√2, cot θ: 1

240°

Radians: 4π/3, sin θ: -√3/2, cos θ: -1/2, tan θ: √3, csc θ: -2√3/3, sec θ: -2, cot θ: √3/3

270°

Radians: 3π/2, sin θ: -1, cos θ: 0, tan θ: undefined, csc θ: -1, sec θ: undefined, cot θ: 0

300°

Radians: 5π/3, sin θ: -√3/2, cos θ: 1/2, tan θ: -√3, csc θ: -2√3/3, sec θ: 2, cot θ: -√3/3

315°

Radians: 7π/4, sin θ: -√2/2, cos θ: √2/2, tan θ: -1, csc θ: -√2, sec θ: √2, cot θ: -1

330°

Radians: 11π/6, sin θ: -1/2, cos θ: √3/2, tan θ: -√3/3, csc θ: -2, sec θ: 2√3/3, cot θ: -√3

360°

Radians: 2π, sin θ: 0, cos θ: 1, tan θ: 0, csc θ: undefined, sec θ: 1, cot θ: undefined

Quadrant I

sin: +, cos: +, tan: +

Quadrant II

sin: +, cos: -, tan: -

Quadrant III

sin: -, cos: -, tan: +

Quadrant IV

sin: -, cos: +, tan: -

Trick for knowing what is positive and negative

ALL STUDENTS TAKE CALCULUS

All are positive in first quadrant

Only Sin is positive in second quadrant

Only Tan is positive in 3rd quadrant

Only cos is positive in 4th quadrant

What is a refrence angle

The angle that is made with the x-axis, use angle with that to find out.

What are coterminal Angles

and why do they matter

Coterminal angles are angles that share the same initial and terminal sides on the unit circle, meaning they end in the same position. You find them by adding or subtracting full rotations: 360 degrees or 2π radians.

All trig function values (sin, cos, tan, etc.) are the same for coterminal angles because they land at the same point on the unit circle.

30° Family (30 degree refrence angle)

30°, 150°, 210°, 330°; π/6, 5π/6, 7π/6, 11π/6; sin: ±½, cos: ±√3/2, tan: ±√3/3

45° Family (45 degree refrence angle)

45°, 135°, 225°, 315°; π/4, 3π/4, 5π/4, 7π/4; sin: ±√2/2, cos: ±√2/2, tan: ±1

60° Family (60 degree refrence angle)

60°, 120°, 240°, 300°; π/3, 2π/3, 4π/3, 5π/3; sin: ±√3/2, cos: ±½, tan: ±√3