AI: CSP Complexities
1/9
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
10 Terms
Naive approach complexity
b = (n - l)d at depth l therefore n!d^n leaves!!!
backtracking complexity
b = d → d^n leaves
so general CSPs O(d^n)
Arc consistency algorithm complexity
O(n²d³) can be reduced to O(n²d²) (AC-3)
complexity when each subproblem has c variables out of n total
O(n/c * dc)
complexity for constraint graph without loops = tree
O(nd²)
choose variable as root, order variables from root to leaves
make arc starting from leaf back to parent
then do assignment starting from root’s first child
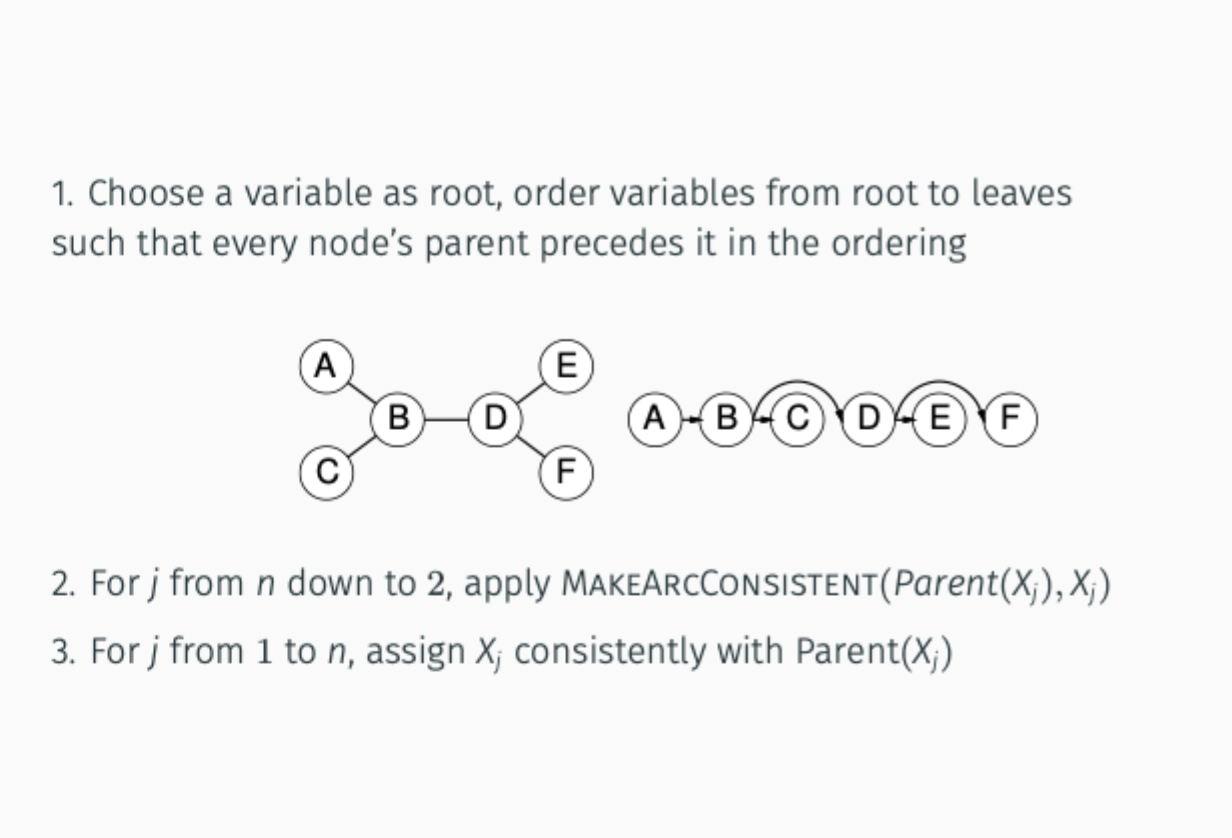
Nearly tree-structured CSP complexity
idea: assign variables and prune neighbour domains such that the constraint graph forms a tree
conditioning: instantiating(assign) variable, prune neighbor’s domain
cutset: a set of variables that can be deleted to that the constraint graph forms a tree
cutset conditioning: instantiate (in all ways) a set of variables such that the remaining constraint graph is a tree
cutset size c → O(dc * (n-c)d²) time, very fast for small c. d² is from tree structured time
Iterative algorithm for CSP: Local Search
Local search: a version of hill-climbing adapted for CSPs.
This is in contrast to backtracking. Local search is often faster and more memory-efficient, especially for large CSPs, though it doesn't guarantee finding a solution.
start with a complete assignment: all variables are assigned values, even if some constraints are violated.
repeatedly improve the current state by changing the value of one variable at a time.
Variable Selection: Randomly select any conflicted variable
Value Selection by Min-Conflicts Heuristic: try all possible values for that variable, and pick the one that results in the fewest violated constraints.
complexity: can solve n-queens in almost constant time for arbitrary n with high prob.
number of constraints / number of variables
essentially hillclimb with h(n) = number of violated constraints
How normal Hill-Climbing Works?
Heuristic function h(n): Estimates how "good" a state is. Lower is better (for minimization).
Start at a random state.
Evaluate neighboring states.
Move to the neighbor that gives the best improvement (e.g., lower cost or more constraints satisfied).
Repeat until no better neighbor exists.
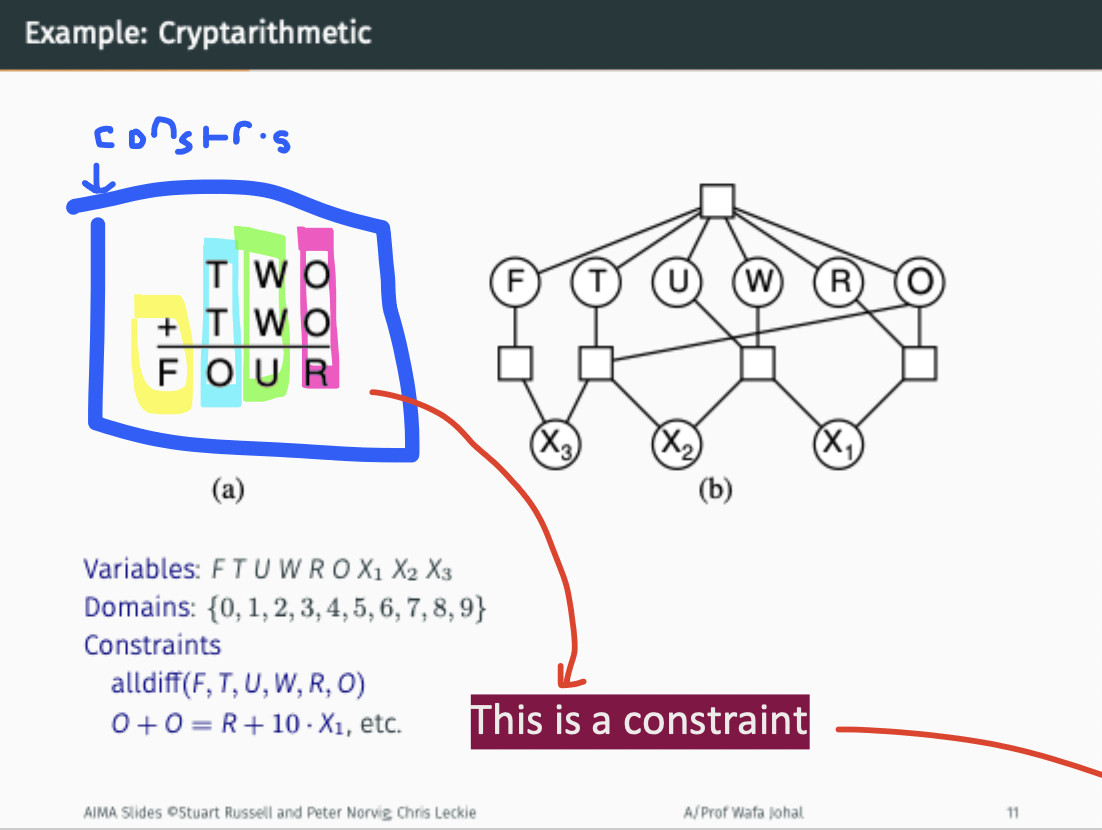
Cryptarithmetic
Alldiff is first constraint
Consider potential carry over X1, X2, X3
The boxes mean they are constraints involving more than 1 variable.
Top box is alldiff
In a general CSP with n variables, each taking d possible values, what is the maxi- mum number of times a backtracking search algorithm might have to backtrack, if it is running arc consistency and applying the Minimum Remaining Values (MRV) and (Least Constraining Value) LCV heuristics?.
O(n²d³)