Light: Wave Model

Waves: Revision

• Definiton

• Representing Waves

• Types of waves

Definition: A propagating disturbance that transport energy through a medium.

• Propagation – way the wave travels/moves

• Medium – matter that a wave moves through

• Oscillate – to move back and forth between two points

  • Waves transfer energy from without moving matter

  • Waves are oscillating particles

Representing Waves

• Wave fronts – a line that represents the crest of the wave (birds eye view of wave)

  • Distance between them is the wavelength

• Rays – a line that shows directions of the wave travels (perpendicular to wavefronts)

  • Angles of rays are measured relative to the normal

Types

• transverse - direction of particle oscillation is perpendicular to propagation

• longitudinal - direction of particle oscillation is parallel to propagation

• mechanical - changing in kinetic and gravitational energy

• EM - change in electric and magnetic energy

Early Classical Models of Light: Huygens vs. Newton

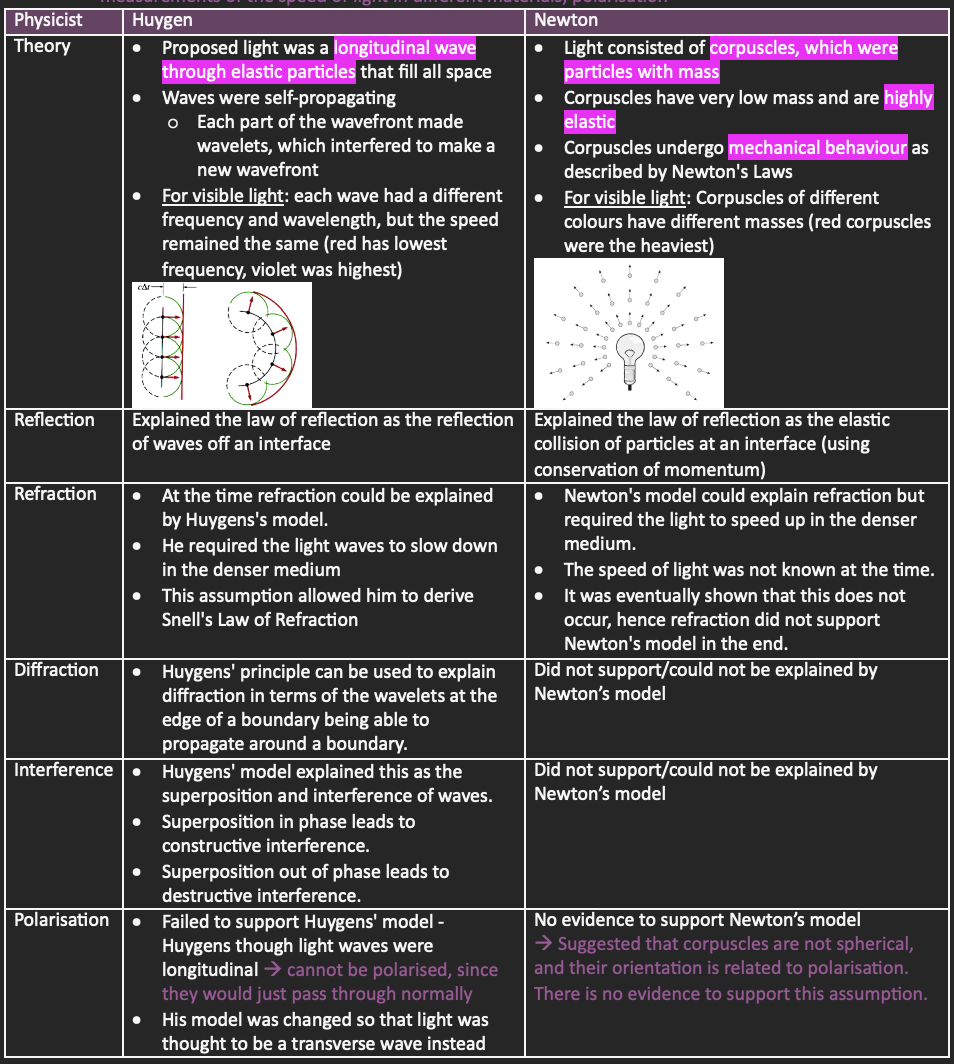
Newton vs Huygens: Reflection

Through observations, light was known to reflect of smooth surfaces following the Law of Reflection: The angle of incidence = the angle of reflection

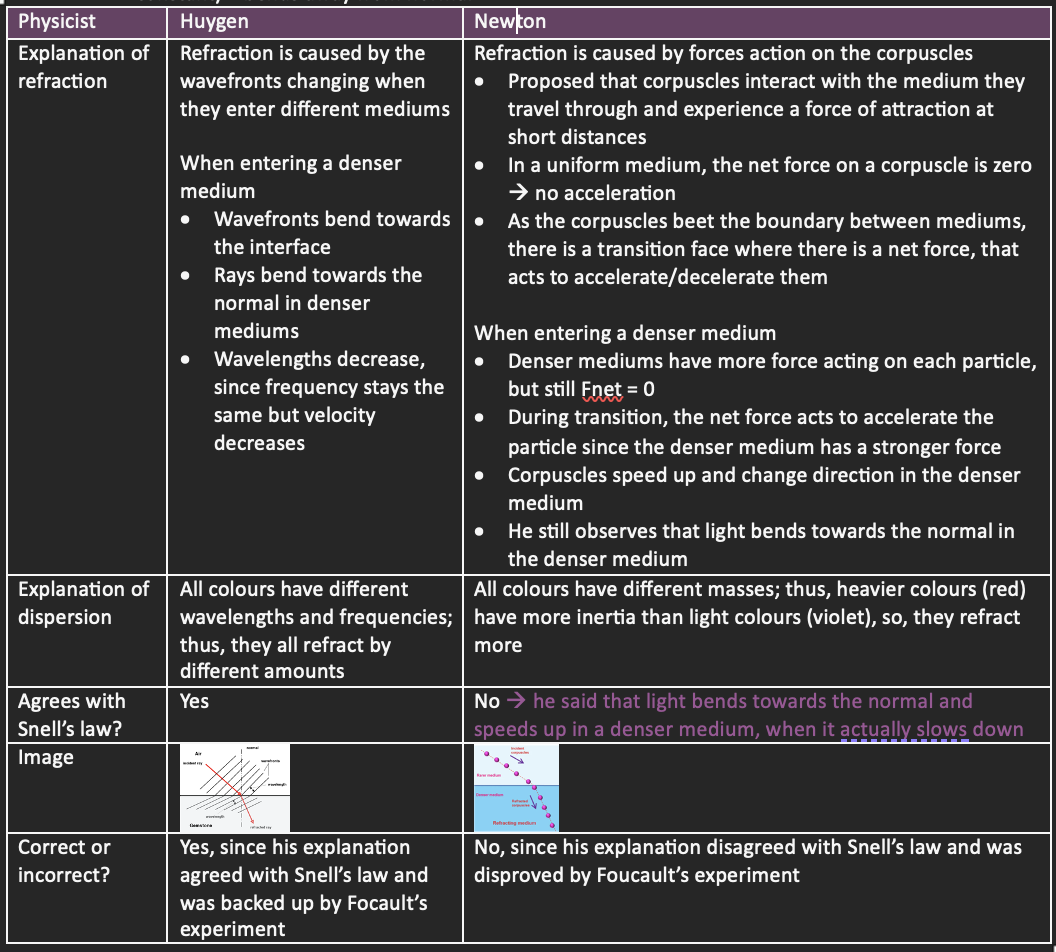
Newton vs Huygens: Refraction

The bending of waves as they travel from one medium into another

• Angle of incidence = 0°, Angle of refraction = 0° (no refraction, but speed will change)

• Frequency stays the same for the incident and refracted waves → v and λ change

Dispersion – when colours refract by different amounts, and spread out into a rainbow

Refraction is described by Snell’s Law:

• Wave moves to denser medium = it slows down (wavelength decreases + frequency stays constant) = bends towards normal

• Wave moves to less dense medium = speeds up (wavelength increases + frequency stays constant) = bends away from normal

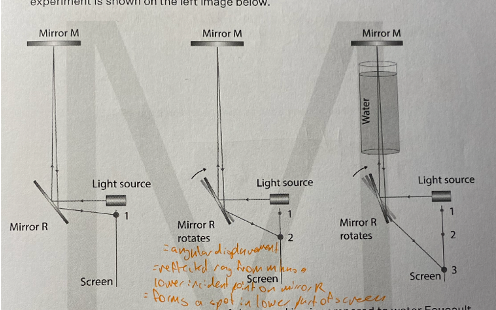
Relative speed of light in air and water

In 1850, Leon Foucault performed an experiment that determining whether light travelled faster in air or water.

Method	A beam of light is reflected off mirror R, to mirror M, back to mirror R After this, the reflected beam reach’s a screen However, light takes time to travel between two points (the reflected and incident light on mirror R) During that time, the mirror rotates (has angular displacement) The reflected light from M being incident on R at a lower position, means that it is then reflected on to the screen at a lower point, than it would if mirror R did not rotate Since, it takes time for light to travel from mirror R, to mirror M, back to mirror R, we can compare the point the beam lands on the screen when putting a different medium between mirror R and M
Result	When travelling through water, light had the lowest point on the screen When travelling through air, light had a higher point on the screen This shows that light travels slower through water, as the mirror R had more time to rotate to a steeper position, and thus have a greater angle of incidence from mirror M
Impact on the model of light	This proved that Newton’s model was incorrect, as he believed light travelled faster in a denser medium, when it in fact, does not.

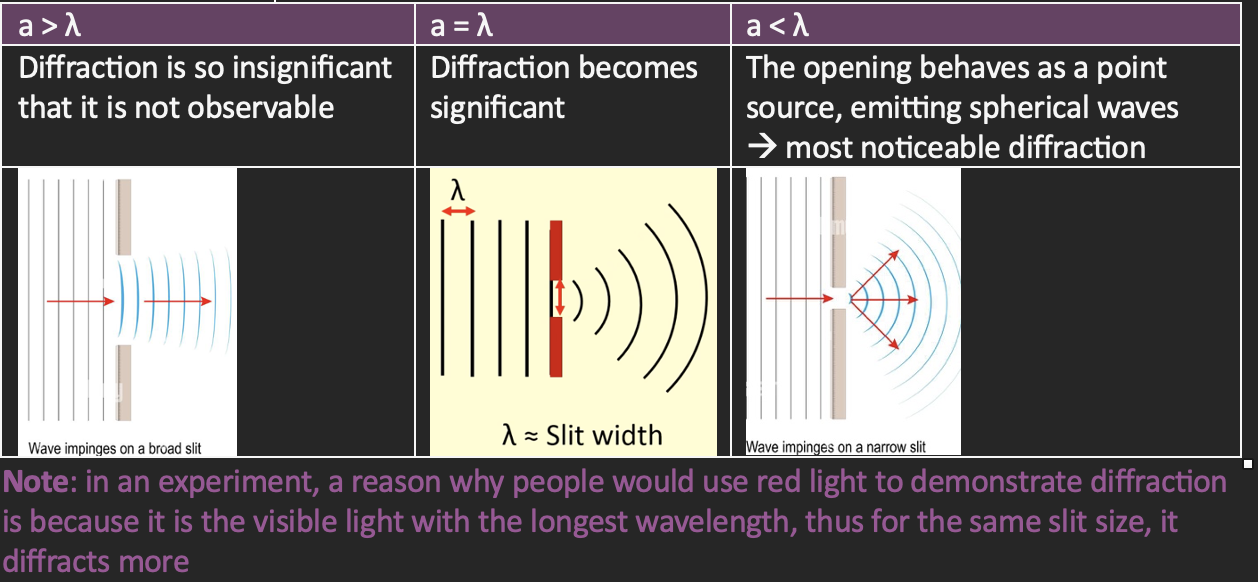
Diffraction of light

the bending of waves around obstacles and through gaps

• Speed, frequency or wavelength don’t change when a sound wave is diffracted

• Diffraction effect is greatest when the width of the gap is about the same size as the wavelength of the wave

• Occurs when a wave: passes an edge, passes through a narrow gap, goes past an object

Explaining diffraction with huygens’ principle

• The wavelets away from the barrier interface interfere and cancel out in all directions other than the forwards direction producing a straight propagating wavefront

• Wavelets hitting the barrier are blocked and produce no waves

• Wavelets near edges that are free to propagate (since there are no other wavelets to interfere with) produce curved wavefronts

Newton’s theory could not explain diffraction

Interference

the superposition of two or more waves

Depending on the relative phase of the superimposed waves, two different types of interference can occur:

• Constructive interference – amplitudes of each wave produce a higher amplitude

• Destructive interference – amplitudes of each wave produce a lower amplitude

Single vs double slit vs diffraction grating

Single	Double	Grating
When light passes through a slit, it diffracts → The closer the aperture is to the wavelength of light, the more obvious diffraction is The slit acts as a new point source of light This point source consists of many self-propagating wavelets which interfere to make a wavefront The most outside wavelets (ones closest to the edge of the gap) cannot interfere with other wavelets since they are blocked, so they spread around to form a curved wavefront The interference of these wavelets makes the diffraction pattern	Thomas Young: Devised in 1801 to demonstrate that light is a wave → light undergoes diffraction and interference (wave phenomena) Allowed light to pass through a double slit barrier Through these slits, the lights diffracted When the light passes through the slits, it acts as a new point source and thus diffracts into smaller wavelets The wavelets will constructively and destructively interfere according to the path difference This forms a series of dark (destructive interference) and bright (constructive interference) fringes Diffraction of white light Produces a repeating rainbow-like spectrum Within each spectrum, longer wavelength of visible light (red) is further away from the centre This is because the angle of diffraction increases for light of longer wavelengths.	We pretend it’s like many double slit experiments next to each other
d = the distance of the gap/aperture (m) m = the ‘order’ of minima (dark fringes)	d= distance between double slit m = order of maxima	d = the distance between two adjacent slits = total distance ÷ number of lines m = the ‘order’ of maxima

Max Number of maxima

• For a particular wavelength of light and distance (d) between slits, the number of orders (m) of bright spots (maxima) is finite

• A maximum cannot form more than 90 degrees from the midline between the two slits.

• Thus, the angle at which the furthest maximum is formed must be smaller than 90°

• Substitute an angle of 90° into the diffraction equation, the greatest order of maxima is given by: m=d/λ

The greatest order is the largest integer lower than the calculated value

Polarisation

the orientation of a wave’s oscillations (its plane of oscillation)

• Proved that light was a transverse wave

• Huygen assumed it was longitudinal, and longitudinal waves cannot be polarised since they are one dimensional (plane of propagation is the same as oscillation), and thus their plane cannot be changed since there is only one

Polarisers – devises that only allows one polarisation of light to be transmitted

• Only allows the component of that wave that is travelling in the same plane as the polariser to pass through

• Linearly polarised – when the oscillation is restricted to one plane

• If polariser is in the same plane as wave oscillations = all of it passes through → intensity remains the same

• If the polariser is perpendicular to the plane of wave oscillations = none of it passes through → intensity is zero

• If unpolarised light passes through a polariser = half of it is passed through → it is 50% of the original intensity

• generally EM waves are polarised according the their electric field’s plane