Chapter 13 - Exponential Functions and Logarithms

Logarithm master in a nutshell!

What is a power, base, and exponent?
List the index laws and key rules for powers.

• A power is written as aⁿ, where:

  • a is the base (non-zero)

  • n is the exponent or index

Index Laws (for a, b ≠ 0 and integers m, n):

a^m \times a^n = a^{m+n}

\frac{a^m}{a^n} = a^{m-n}

(a^m)^n = a^{mn}

(ab)^n = a^n \times b^n

\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}

Special rules:

• a^0 = 1 \quad (a \neq 0)

  a^{-n} = \frac{1}{a^n}, \quad \frac{1}{a^{-n}} = a^n

  0^n = 0 \quad \text{for } n > 0, \quad 0^0 \text{ is undefined}

What does a^{\frac{1}{n}} mean?
How do index laws extend to rational indices?

• For a > 0 and n ∈ ℕ:
  a^{\frac{1}{n}} = \sqrt[n]{a} \quad \Rightarrow \quad \left(a^{\frac{1}{n}}\right)^n = a

• Special cases:

  • 0^{\frac{1}{n}} = 0

  • If n is odd and a < 0, a^{\frac{1}{n}}is defined (result is negative)

Extended Index Laws:

a^{\frac{m}{q}} \times a^{\frac{n}{p}} = a^{\frac{m}{q} + \frac{n}{p}}

\frac{a^{\frac{m}{q}}}{a^{\frac{n}{p}}} = a^{\frac{m}{q} - \frac{n}{p}}

\left(a^{\frac{m}{q}}\right)^{\frac{n}{p}} = a^{\frac{m}{q} \times \frac{n}{p}}

Exponential Functions & Transformations

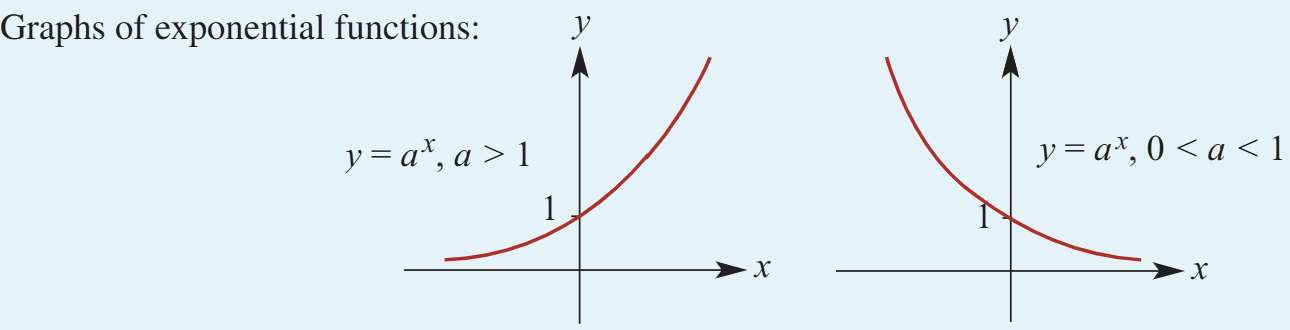
• For y = aˣ where a > 1, the graph has:

  • The x-axis as an asymptote.

  • A y-intercept at (0, 1).

  • Positive y-values with no x-axis intercept.

  • All graphs of this form are dilations of each other from the y-axis.

• For y = aˣ where 0 < a < 1, the graph decays similarly but reflects the opposite behavior.

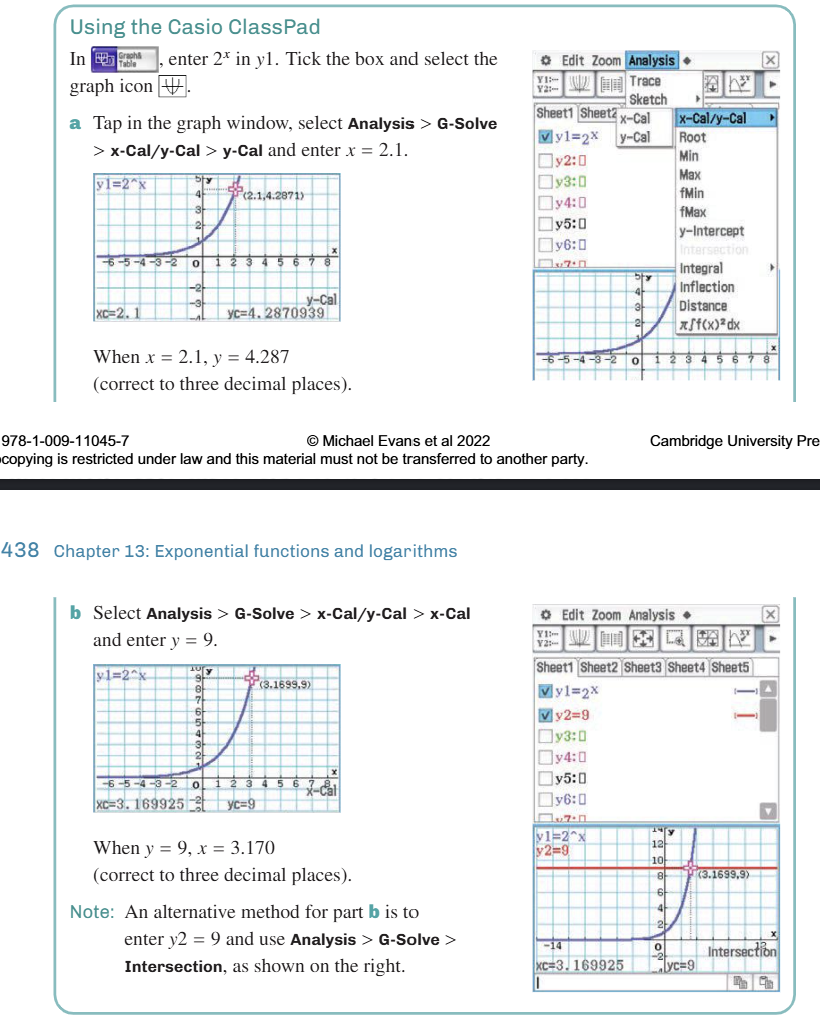
• If f(x) = aˣ and g(x) = a⁻ˣ, then g(x) is the reflection of f(x) in the y-axis.

CAS: Sketching Logarithm Graphs

Solving Exponential Inequalities

To solve an exponential equation without a calculator, express both sides with the same base and equate the exponents (since aˣ = aʸ implies x = y for any base a > 0, a ≠ 1).

Example: 2^{x+1} = 8 \Rightarrow 2^{x+1} = 2^3 \Rightarrow x + 1 = 3 \Rightarrow x = 2

To solve an exponential inequality, follow the same method as an equation and apply the appropriate property:

If a^x > a^y, then:

x > y \quad \text{when} \quad a > 1

x < y \quad \text{when} \quad 0 < a < 1

Laws of Logarithms

• For a ∈ R⁺ \ {1}, the logarithm function base a is defined as follows:
  aˣ = y is equivalent to log_ay = x.

• The expression log_ay is defined for all positive real numbers y.

• To evaluate log_ay, ask the question: "What power of a gives y?"

Laws of Logarithms:

\log_a(mn) = \log_a m + \log_a n

\log_a\left(\frac{m}{n}\right) = \log_a m - \log_a n

\log_a(m^p) = p \log_a m

\log_a(m^{-1}) = - \log_a m

\log_{\frac{1}{a}}(x) = -\log_a x

Specials:

• \log_a 1 = 0 \quad \text{and} \quad \log_a a = 1

Using logarithms to solve exponential equations and inequalities

Key Concepts:

• Logarithmic Relationship:
  For a, b, c > 0, where a ≠ 1 and b ≠ 1, we have:
  \log_a c = \frac{\log_b c}{\log_b a}

• Logarithms and Exponentials:
  If a \in \mathbb{R}^+ \setminus \{1\}and x ∈ R then:

  • a^x = b \Leftrightarrow \log_a b = x

  This property is useful for solving exponential equations and inequalities.

• Examples:

  2^x = 5 \iff x = \log_2 5

  2^x \geq 5 \iff x \geq \log_2 5

  (0.3)^x = 5 \iff x = \log_{0.3} 5

  (0.3)^x \geq 5 \iff x \leq \log_{0.3} 5

Examples of Solving Exponential Equations

• Solve 2ˣ = 11:
  x = log₂ 11 ≈ 3.45943.

• Alternative Method:
  Taking log₁₀ of both sides:

  • \log_{10}(2^x) = \log_{10} 11 \Rightarrow x \log_{10} 2 = \log_{10} 11 \Rightarrow x = \frac{\log_{10} 11}{\log_{10} 2}

    \therefore \log_2 11 = \frac{\log_{10} 11}{\log_{10} 2}

• Solve 3²ˣ⁻¹ = 28:

  • 2ˣ - 1 = log₃ 28

  • 2ˣ = 1 + log₃ 28

  • x ≈ 2.017.

• Solve the inequality 0.7ˣ ≥ 0.3:
  Taking log₁₀ of both sides:

  • x \log_{10} 0.7 \geq \log_{10} 0.3 \quad \Rightarrow \quad x \leq \frac{\log_{10} 0.3}{\log_{10} 0.7}

  • x ≈ 3.376 (direction of inequality reversed since log₁₀ 0.7 < 0).

  Alternatively, solve as:
  x ≤ log₀.₇ 0.3.

Exponential Graphs and Logarithms

• Graph of f(x) = 2 × 10ˣ − 4:

  • Horizontal asymptote at y = −4 as x → −∞.

  • The y-axis intercept is f(0) = −2.

  • The x-axis intercept occurs when f(x) = 0:

    • 2 × 10ˣ − 4 = 0 → x = log₁₀ 2 ≈ 0.3010.

📊 Properties of Exponential vs Logarithmic Functions

Property	y = aˣ (Exponential)	y = logₐx (Logarithmic)
Domain	ℝ	ℝ⁺ (x > 0)
Range	ℝ⁺ (y > 0)	ℝ
Key Point	a⁰ = 1	logₐ1 = 0
End Behavior	x → −∞, y → 0⁺	x → 0⁺, y → −∞
Asymptote	y = 0	x = 0

🔄 Transformations Summary (General Form)

Type	Example	Effect
Shift Right	y = logₐ(x − h)	→ right h units
Shift Left	y = logₐ(x + h)	→ left h units
Shift Up	y = logₐ(x) + k	↑ up k units
Shift Down	y = logₐ(x) − k	↓ down k units
Stretch (vertical)	y = a·logₐ(x), a > 1	↑ vertical stretch by factor a
Compress (vertical)	y = a·logₐ(x), 0 < a < 1	↓ vertical compression by factor a
Horizontal Compress	y = logₐ(bx), b > 1	→ compress across y-axis (divide x by b)
Horizontal Stretch	y = logₐ(bx), 0 < b < 1	→ stretch across y-axis (multiply x by 1/b)
Reflect in x-axis	y = −logₐ(x)	↩ reflect in x-axis
Reflect in y-axis	y = logₐ(−x)	↪ reflect in y-axis

🔁 Inverse Functions:

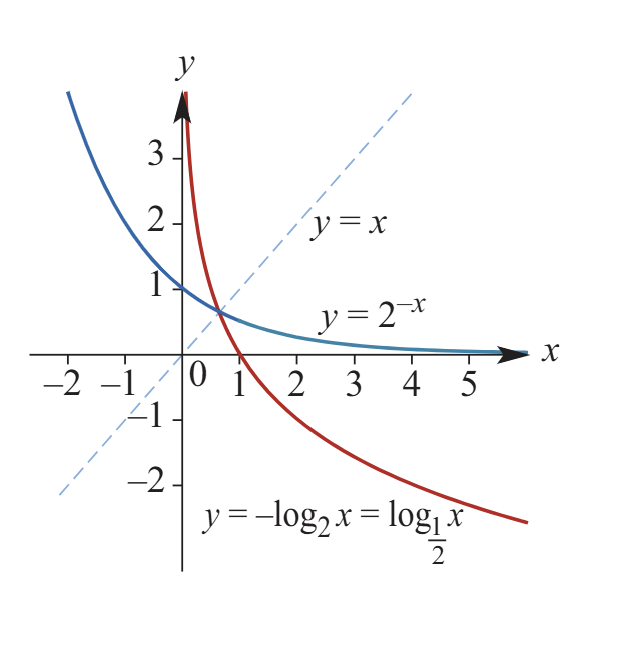
y = a^x \iff x = \log_a y
↔ Reflect across the line y = x

If a > 0 and a ≠ 1, then:

\log_a (a^x) = x \quad \text{for all real } x

a^{\log_a x} = x \quad \text{for all positive } x

Exponential Modelling (General)

In exponential change, let A be the quantity at time t. The general formula is:

• A = A_0 b^t

  where A₀ is the initial quantity and b is a positive constant.

  • If b > 1, the model represents growth, such as:

    • Growth of cells

    • Population growth

    • Continuously compounded interest

  • If b < 1, the model represents decay, such as:

    • Radioactive decay

    • Cooling of materials

Application and Variants of the Model

• Cell Growth Formula:
  For bacterial growth, the formula N = N_0 2^{\frac{t}{T_D}}is used, where Tᴰ is the generation time.

• Radioactive Decay Formula:
  The formula A = A_0 2^{-kt} describes radioactive decay, where k is the decay constant. Half - life may be used to model this A = A_0 \left(\frac{1}{2}\right)^n

• Population Growth:

• A = A_0 \left(1 + \frac{r}{100}\right)^t
  Where:

  • A = population

  • A₀ = initial population

  • r = rate of growth/decay

  • t = time taken

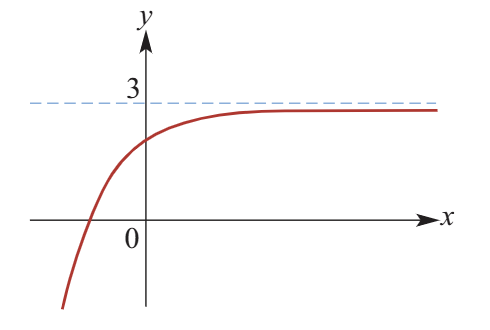
Limiting Values

In some exponential functions, a limiting value L is approached but never reached. Using the concept of limit, the formula for this behavior can be written as:
\lim_{x \to \infty} f(x) = L
where f(x) approaches L as x increases but never actually reaches it.

CAS: Determining Rules

1. Define f(x) = a × bx.

2. Solve the simultaneous equations (in example).

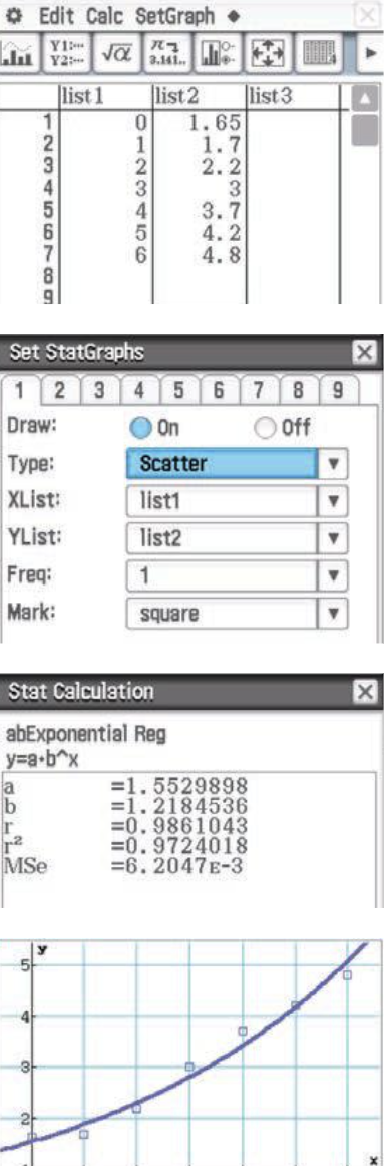
CAS: Fitting Data (Example)

• Enter the data into List1 and List2.

• Set the graph type to Scatter and assign List1 and List2 to the graph.

• Tap Set to display the scatter plot.

• Select Calc > Regression > abExponential Reg and tap OK to confirm.

• The exponential function w = 1.55(1.22)ᵐ models Somu’s weight.

• Tap OK to view the graph of the regression curve.

Where are the asymptotes for transformed functions y = a^(x-h) + k and y = logₐ(x − h) + k?

• Exponential y = a^(x-h) + k → Horizontal asymptote y = k

• Logarithmic y = logₐ(x − h) + k → Vertical asymptote x = h