AP Stats Conditional Probability and Independent.

Conditional Probability

When extra (given) info is presented that affects how much of the overall data is to be considered.

P( A | B )

This is to be read as,

“the probability of event A given event B has occurred.”

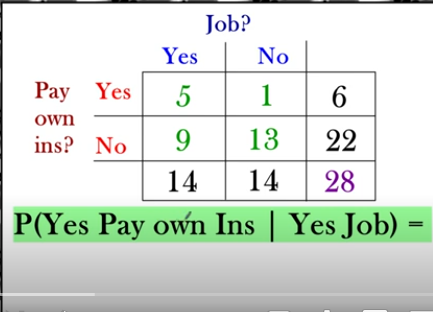
Example: Two Way table that presents amount of students that have a job and pay their own car insurance

P( Yes Pay own Car insurance | Yes Job )

P (Yes Pay own Car Ins / Yes Job ) = 5/14

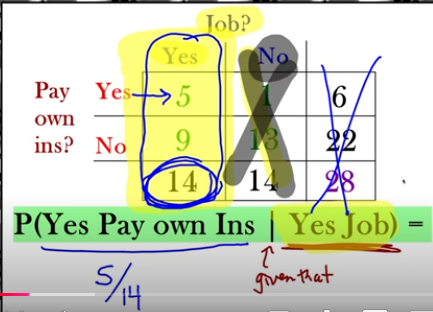
On the Pink formula:

P (A | B) = P(A ∩ B) → ∩ = and divided by P(B) = 5/28 divided by 14/28

= 5/14

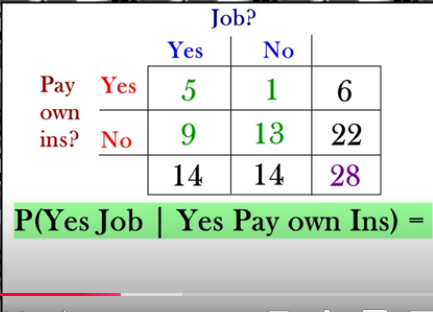
P( Yes Job | Yes Pay own Ins )

Find probability that yes they have a job, given that they pay for their own car insurance.

5/6!!! (only pay attention to the given row on the data table)

Does having a job affect the probability that a student will have to pay their own insurance?
P( Yes Pay own Ins_ = 5/28 = 21.4%

P(Yes Pay own Ins / Yes Job ) 5/14 = 35.6%

P(Yes Pay own Ins/ No Job ) = 1/14 = 7.1% (smaller value)

YES! If a student had a job, then they were more likely to pay for their own insurance

We can say that having a job and paying his/her own insurance are DEPENDENT EVENTS all because mathematically..

P(Yes Pay) =/ P(Yes Pay | Yes Job)

Values not equal to eachother

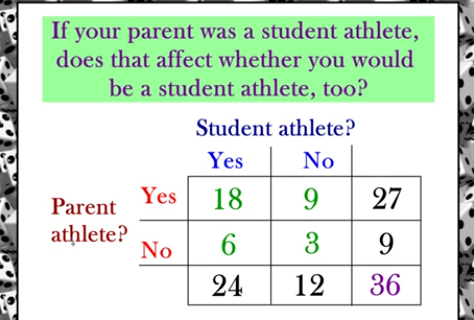
If your parent was a student althete, does that affect whether you would be a student athlete too?

P(Yes student Athlete) =

P(Yes Student | Yes Parent) =

P(Yes Student | No Parent)=

P(Yes student Athlete) = 24/36 = 0.66

P(Yes Student | Yes Parent) = 18/27 = 0.66

P(Yes Student | No Parent)= 6/9 = 0.66

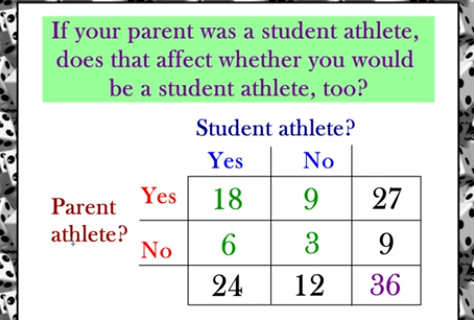
If your parent was a student athlete, does that affect whether you would be a student athlete, too?

NO!!! If the parent was an athlete or not did not affect the probability the student is an athlete

We can conclude your parents decision to be a student athlete and your decision to be a student athlete are INDEPENDENT EVENTS all because mathematically…

P(Yes Student Athlete) = P( Yes Student | Yes Parent )

Values are equal to each other

P(A | B) = P(A)