Statistics and Machine Learning 1

Law of total probability

P(B) = P(B|A₁) . P(A₁) + P(B|A₂) . P(A₂) + … + P(B|A_n) . P(A_n)

Bayes theorem

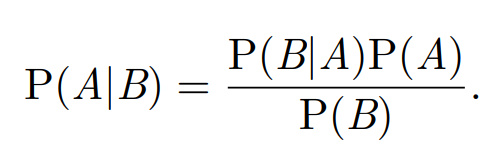
What is Bernoulli distribution?

Discrete probability distribution that models a single experiment with only two possible outcomes.

If P(X = 1) = q then P(X = 0) = 1 - q

How to calculate the mean and variance of a Bernoulli distribution?

Mean(X) = E(X)

• Mean(X) = q

Var(X) = E[X²] - E[X]²

• Var(X) = q - q²

What is the binomial distribution?

Discrete probability distribution that represents the outcome of n independent trials. Its PMF Bin(k | n, q) is the probability of k positive outcomes in n trials given a positive outcome probability q.

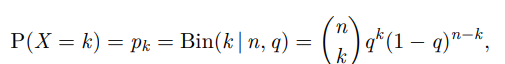
What are the mean and variance for a binomial distribution?

Mean(X) = nq

Var(X) = nq(1-q)

What is the poisson distribution?

Discrete probability distribution that represents the number of events that can happen with a ‘rate’ λ.

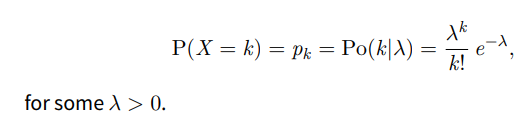
What are the mean and variance of a poisson distribution?

Mean(X) = λ

Var(X) = λ

What is the beta distribution?

Continuous distribution used to represent uncertainty in proportions

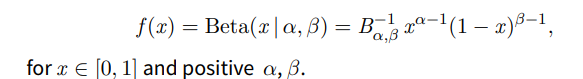
What is the normalising constant of the beta distribution and how is it calculated?

B^-1_α,β. Chosen so P(0 <= x <= 1) = 1. Calculated with an integral.

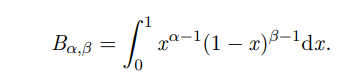
What are the mean and variance of the beta distribution?

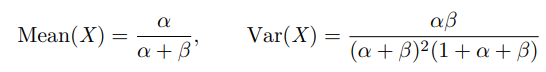
What is the gamma distribution and how is it calculated?

Continuous probability distribution used to model times between events

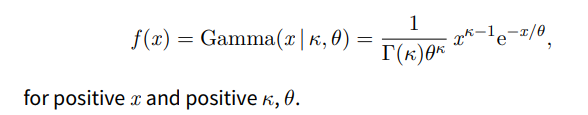
What are the mean and variance of the gamma distribution?

Mean(X) = κθ

Var(X) = κθ²

In the gamma distribution, what happens if k = 1

Creates exponential distribution, or the distribution of times between events for a memoryless process

Suppose we have two random variables, X₁ and X₂ that are independent and are both normally distributed with means µ₁ and µ₂ and variances σ²₁ and σ²₂ , respectively.

1. What is the mean and variance of X₁ + X₂?

2. What is the mean and variance of aX₁ + b

1. Mean = µ₁ + µ₂ Var = σ²₁ + σ²₂

2. Mean = aµ₁ + b Var = a²o²₁