Algebra

Relazione di Charles o regola del parallelogramma

a + b = AB + CD = AB + BX = AX

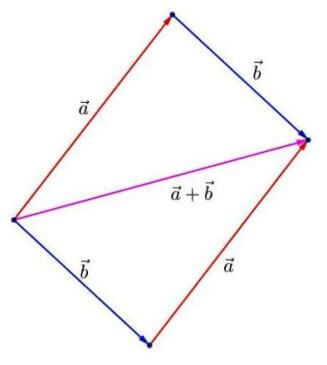
Proprietà dell’addizione vettoriale in E₃

1. Proprietà associativa,

2. Proprietà commutativa,

3. Esistenza dell’elemento neutro,

4. Esistenza dell’opposto.

Proprietà della moltiplicazione per uno scalare

1. Esistenza dell’elemento neutro (1)

2. Una specie di proprietà associativa della moltiplicazione di due numeri per un vettore libero,

3. Una specie di proprietà distributiva della moltiplicazione di un vettore libero nella somma di due scalari,

4. Una specie di proprietà distributiva della moltiplicazione di uno scalare nella somma di due vettori liberi.

Relazione equivalenti

Due segmenti orientati AB e CD si dicono equipollenti se hanno stessa lunghezza, direzione e verso.

Spazio vettoriale

Uno spazio vettoriale è un insieme non vuoto i cui elementi si dicono vettori, sul quale sono definite due operazioni:

• addizione vettoriale,

• moltiplicazione per uno scalare

tali che siano soddisfatte le seguenti 8 proprietà:

1. associativa,

2. commutativa,

3. esistenza del neutro,

4. esistenza dell’opposto,

5. 1u=u

6. Una specie di proprietà associativa della moltiplicazione di due numeri per un vettore libero,

7. Una specie di proprietà distributiva della moltiplicazione di un vettore libero nella somma di due scalari,

8. Una specie di proprietà distributiva della moltiplicazione di uno scalare nella somma di due vettori liberi.

Modelli fondamentali di spazio vettoriale

1. Spazio vettoriale Kⁿ di tutte le n-ple ordinate di elementi (scalari) del campo K. (addizione vettoriale e moltiplicazione per uno scalare).

2. Spazio vettoriale delle funzioni a valori in un campo numerico, sia X un insieme non vuoto diverso da 0 (addizione vettoriale e moltiplicazione per uno scalare).

3. Spazio vettoriale delle matrici di tipo (m,n) sul campo numerico K. (addizione vettoriale e moltiplicazione per uno scalare).

Regole di calcolo in uno spazio vettoriale su K

1. 0u=0

2. λ0=0

3. -1(u)=-u

4. -λ(u)=λ(-u)=-λu

5. Legge di annullamento della moltiplicazione di uno scalare per un vettore λu = 0 se e solo se λ=0 o u = 0

6. Legge di cancellazione della moltiplicazione di uno scalare per un vettore

   λu = λv, λ ≠ 0 allora u = v

   λu = μv, u ≠ 0 allora λ = μ

Sottospazio vettoriale

Sia V uno spazio vettoriale sul campo K. Sia W un sottoinsieme non vuoto di V. Allora W è un sottospazio vettoriale di V se soddisfa le seguenti condizioni:

1. Per ogni u,v appartenenti a W si ha che u+v appartiene a W,

2. Per ogni λ appartenente a K, per ogni u appartenente a W si ha che λu appartiene a W.

In alternativa è possibile utilizzare la seguente definizione equivalente:

Per ogni λ, μ appartenenti a K, per ogni u,v appartenenti a W si ha che λu + μv appartiene a W.

Costruzioni fondamentali di sottospazio vettoriale

1. sottospazio vettoriale intersezione: l’intersezione di due sottospazi vettoriali è ancora un sottospazio vettoriale,

2. spazio vettoriale generato da un insieme di vettori (SPAN): sia V uno spazio vettoriale e sia A un sottoinsieme di vettori di V e sia SPAN(A) l’insieme di tutte le combinazioni lineari dei vettori di A.

   Teorema: SPAN(A) è un sottospazio vettoriale di V, detto il sottospazio vettoriale generato da A che soddisfa queste proprietà:

   • A ⊂ SPAN(A),

   • SPAN(A) è il più piccolo sottospazio vettoriale che contiene A.

3. sottospazio vettoriale somma (somma diretta): la somma di due sottospazi vettoriali, W₁ + W₂, è il più piccolo sottospazio vettoriale che contiene W₁U W_2. Ergo W₁ + W₂ = SPAN (W₁U W₂).

   Se W₁ ∩ W₂ = {0} allora la somma si chiama somma diretta e si scrive W₁ + W₂ = W₁ ⊕ W₂.

In generale l’unione di due sottospazi vettoriali non è un sottospazio vettoriale.

Vettori linearmente dipendenti

Si dice che i vettori u₁,u₂,…,u_n sono linearmente dipendenti se esistono n scalari λ¹,λ²,…,λⁿ appartenenti ad R non tutti nulli, tali che la combinazione lineare dei vettori dati con questi scalari dà il vettore nullo.

Vettori linearmente indipendenti

Si dice che i vettori u₁,u₂,…,u_n sono linearmente indipendenti se l’unica combinazione lineare dei vettori dati che dà il vettore nullo si ottiene per scalari tutti uguali a zero.

Proprietà della lineare dipendenza e indipendenza

1. Siano u₁,u₂,…,u_n n vettori di V. Siano m (< n) vettori fra di loro linearmente dipendenti, allora tutti gli n vettori dati sono linearmente dipendenti.

   Proposizione (contronominale): Se u₁,u₂,…,u_n sono linearmente indipendenti allora comunque presi m<n fra di essi restano linearmente indipendenti.

2. Un vettore u è linearmente indipendente se e solo se u≠0. Un vettore u è linearmente dipendente se e solo se u = 0.

3. u,v sono linearmente indipendenti se e solo se u//v cioè esiste ρ appartenente a K tale che v = ρu.

4. Condizione necessaria e sufficiente affinché n vettori dati siano linearmente dipendenti è che uno di essi sia combinazione lineare dei precedenti.

Base di uno spazio vettoriale

Sia V₁ spazio vettoriale finitamente generato, una base B di V è un sottoinsieme non vuoto tale che soddisfa le seguenti condizioni:

• V = SPAN(B)

• B linearmente indipendente

Teorema della base

Sia V uno spazio vettoriale che non si riduce al solo vettore nullo, finitamente generato allora esistono basi in V.

Teorema della dimensione

Tutte le basi di V hanno lo stesso numero di vettori (hanno la stessa cardinalità).

Dimensione di uno spazio vettoriale

Si definisce dimensione di V:

• dim V = 0 se V = {0},

• dim V = numero dei vettori di una base di V se V ≠ {0}.

Regola per esercizi

dim W = numero di variabili indipendenti = dim spazio ambiente - numero di equazioni indipendenti

Proprietà delle basi

Sia V uno spazio vettoriale con dimV=n valgono le seguenti proprietà:

1. tutte le basi di V hanno n vettori,

2. ogni insieme di generatori per V formato da n vettori è una base,

3. ogni insieme di vettori linearmente indipendenti è una base di V,

4. ogni insieme di m vettori linearmente indipendenti con m<n si prolunga ad una base,

5. da ogni insieme di generatori può esistere una base.

Formula di Grassmann per i sottospazi vettoriali

dim (W₁ + W₂) + dim (W₁ ∩ W₂) = dim W₁ + dim W₂

Caso particolare: somma diretta

Quando W₁ ∩ W₂ = {0}

dim(W₁ ⊕ W₂) = dim W₁ + dim W₂

Base ordinata

Sia V uno spazio vettoriale con dim V = n. Una base ordinata è una base di V in cui è fissato un ordinamento tra i vettori, cioè:

B=(e₁,e₂,...,e_n).

Teorema

Sia V uno spazio vettoriale di dimensione n e sia B = (e₁,e₂,...,e_n) una base ordinata di V. Per ogni vettore u appartenente a V esiste ed è unica un’ n-pla di scalari (λ¹,λ²,…,λⁿ ) appartenenti a Kⁿ detta la n-pla delle componenti del vettore u rispetto alla base ordinata B tale che:

u = λ¹e₁ + λ²e₂ + … + λⁿe_n