Fundamentals of Data Representation

Topic 3

what is decimal/base 10

• Decimal is a number system that is made up of 10 digits (0-9)

• Decimal is referred to as a base-10 number system

• Each digit has a weight factor of 10 raised to a power, the rightmost digit is 1s (10⁰), the next digit to the left 10s (10¹) and so on

what is binary/base 2

• Binary is a number system that is made up of two digits (1 and 0) 

• Binary is referred to as a Base-2 number system

• Each digit has a weight factor of 2 raised to a power, the rightmost digit is 1s (2⁰), the next digit to the left 2s (2¹) and so on

example of binary

why do computers use binary

• The CPU is made up of billions of tiny transistors, transistors can only be in a state of on or off

  • Computers use binary numbers to represent data (1 = on, 0 = off)

hexidecimal

is a number system that is made up of 16 digits, 10 numbers (0-9) and 6 letters (A-F)

hexidecimal table

why is hex prefered

• often preferred when working with large values

• It takes fewer digits to represent a given value in hexadecimal than in binary

• It is beneficial to use hexadecimal over binary because:

  • The more bits there are in a binary number, the harder it is to read

    • Numbers with more bits are more prone to errors when being copied

bit pattern

• is a collection of binary numbers

• Everything in a computer has to be stored as a series of 1s and 0s

• The way the computer interprets the numbers determines the outcome

• Examples of this include

  • Representing ASCII characters

  • A hexadecimal value

  • An image

conversion between binary and decimal

draw out the table and lay the number into it, can go either way.

decimal to hex

• To convert the decimal number 28 to hexadecimal, start by converting the decimal number to binary

• Split the 8 bit binary number into two 4 bit numbers (nibbles) as shown below

• Convert each nibble to its decimal value

• 0001 = 1 and 1100 = 12

• Using the comparison table, the decimal value 1 is also 1 in hexadecimal whereas the decimal value 12 is represented in hexadecimal as C

  • decimal 28 is 1C in hexadecimal

units of data

• Computers use binary numbers to represent data

• Data such as characters, images and sound must be stored as binary

• The smallest unit of data a computer can store is 1 binary digit, otherwise expressed as 1 bit

• 1 bit can only hold one value (2¹), this is not big enough to store all kinds of data, so computers have different 'Units of Data'

what is a unit of data

• is a term given to describe different amounts of binary digits stored on a digital device

• These are the units you need to know for GCSE:

Unit	Symbol	Binary	Written as	Example
Bit	b	1 or 0
Byte	B	8 b		A single character
Kilobyte	kB	1000 B (210)	Thousand bytes	A small text file
Megabyte	MB	1000 KB (220)	Million byes	A music file
Gigabyte	GB	1000 MB (230)	Billion bytes	A high definition movie
Terabyte	TB	1000 GB (240)	Trillion bytes	A large hard drive

conversions between units of data

	Unit
Multiply by 8 ⇑	Bit	Divide by 8 ⇓
	Byte
Multiply by 1000 ⇑	Kilobyte	Divide by 1000 ⇓
	Megabyte
	Gigabyte
	Terabyte
	Petabyte

binary addition

is the process of adding together up to three binary integers (up to and including 8 bits)

golden rules of binary addition

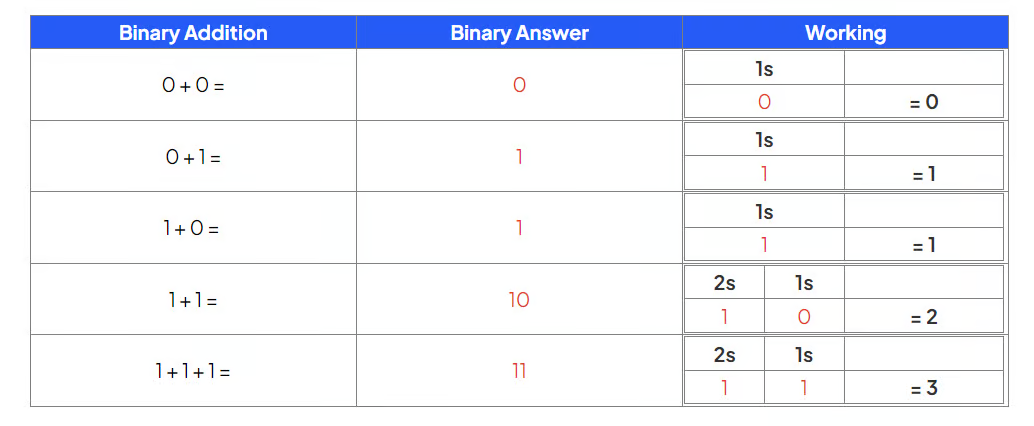
overflow error

• occurs when the result of a binary addition exceeds the available bits

• For example, if you took binary 11111111 (255) and tried to add 00000001 (1) this would cause an overflow error as the result would need a 9th bit to represent the answer (256)

binary shift

• is how a computer system performs basic multiplication and division

• Binary digits are moved left or right a set number of times

• A left shift multiplies a binary number by 2 (x2)

• A right shift divides a binary number by 2 (/2)

• A shift can move more than one place at a time, the principle remains the same

• A left shift of 2 places would multiply the original binary number by 4 (x4)

left shift

multiply by 2

right shift

divide by 2 `

left shift of 2

multiply by 4

right shift of 2

divide by 4

what is a character set

• is a defined list of characters that can be understood by a computer 

• Each character is given a unique binary code

• Character sets are ordered logically, the code for ‘B’ is one more than the code for ‘A’

• A character set provides a standard for computers to communicate and send/receive information

• Without a character set, one system might interpret 01000001 differently from another

• The number of characters that can be represented is determined by the number of bits used by the character set

• Two common character sets are:

  • American Standard Code for Information Interchange (ASCII)

  • Universal Character Encoding (UNICODE)

ascii

• ASCII is a character set and was an accepted standard for information interchange

• ASCII uses 7 bits, providing 2⁷ unique codes (128) or a maximum of 128 characters it can represent

• ASCII only represents basic characters needed for English, limiting its use for other languages

unicode

• UNICODE is a character set and was created as a solution to the limitations of ASCII

• UNICODE uses a minimum of 16 bits, providing 2¹⁶  unique codes (65,536) or a minimum of 65,536 characters it can represent

• UNICODE can represent characters from all the major languages around the world

ascii vs unicode

	ASCII	UNICODE
Number of bits	7-bits	16-bits
Number of characters	128 characters	65,536 characters
Uses	Used to represent characters in the English language.	Used to represent characters across the world.
Benefits	It uses a lot less storage space than UNICODE.	It can represent more characters than ASCII.  It can support all common characters across the world. It can represent special characters such as emoji's.
Drawbacks	It can only represent 128 characters.  It cannot store special characters such as emoji's.	It uses a lot more storage space than ASCII.

what is a bitmap

• is made up of squares called pixels, meaning picture elements

• A pixel is a single point in a image

• Each pixel is stored as a binary code

• Binary codes are unique to the colour in each pixel

• A typical example of a bitmap image is a photograph

what is image size

• is the total amount of pixels that make up a bitmap image

• The image size is calculated by multiplying the height and width of the image (in pixels)

• In general, the higher the image size the more detail in the image (higher quality)

what is colour depth

• is the number of bits stored per pixel in a bitmap image

• The colour depth is dependent on the number of colours needed in the image

• In general, the higher the colour depth the more detail in the image (higher quality)

• In a black & white image the colour depth would be 1, meaning 1 bit is enough to create a unique binary code for each colour in the image (1=white, 0=black)

colour depth

• As colour depth increases, so does the amount of colours available in an image

• The amount of colours can be calculated as 2ⁿ (n = colour depth) 

Colour Depth	Amount of Colours
1 bit	2 (B&W)
2 bit	4
4 bit	16
8 bit	256
24 bit	16,777,216 (True Colour)

impact of image size and colour depth

• As the image size and/or colour depth increases, the bigger the size of the file becomes on secondary storage

• The higher the image size, the more pixels are in the image, the more bits are stored

• The higher the colour depth, the more bits per pixel are stored

• Striking a balance between quality and file size is always a consideration

bitmap file size

• Calculating the size of a bitmap image is carried out with the following formula:

  • Image size x colour depth OR

  • Image width x image height x colour depth

what is metadata

• is data about data

• Metadata is additional information stored with the image, it provides context and information

• Examples of metadata that are stored are:

  • Image size

  • Colour depth

  • Author - Who created the image?

  • Date/Time - When and what time was the image created/taken?

  • Location - Where was the image taken?

how is sound sampled and stored

• Measurements of the original sound wave are captured and stored as binary on secondary storage

• Sound waves begin as analogue and for a computer system to understand them they must be converted into a digital form

• This process is called Analogue to Digital conversion (A2D)

• The process begins by measuring the amplitude of the analogue sound wave at a point in time, called samples

• Each measurement (sample) generates a value which can be represented in binary and stored

• Using the samples, a computer is able to create a digital version of the original analogue wave

• The digital wave is stored on secondary storage and can be played back at any time by reversing the process

what is sample rate

• is the amount of samples taken per second of the analogue wave

• Samples are taken each second for the duration of the sound

• The sample rate is measured in Hertz (Hz)

• 1 Hertz is equal to 1 sample of the sound wave

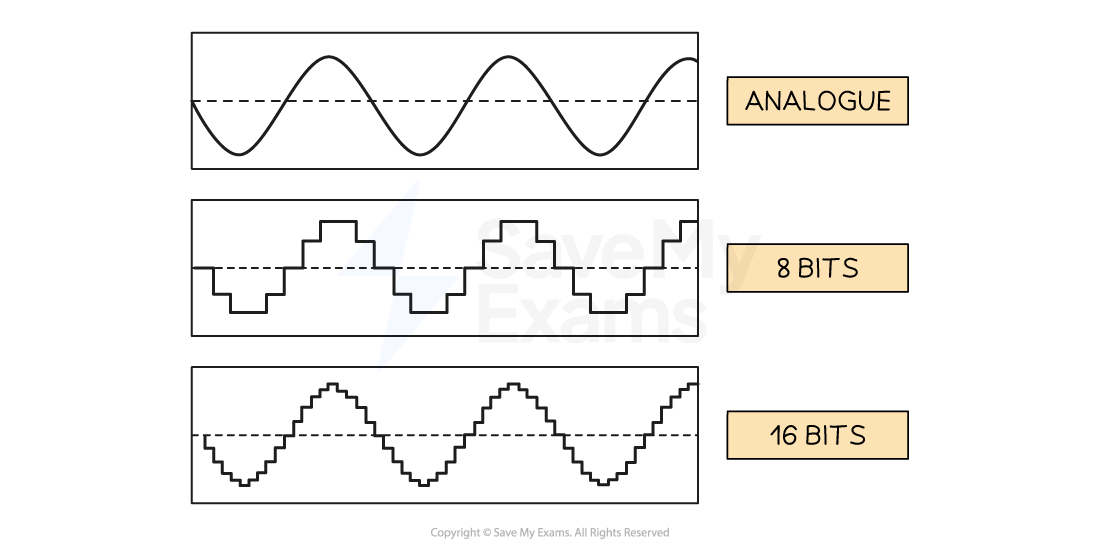
what is sample resolution

• Sample resolution is the number of bits stored per sample of sound

• Sample resolution is closely related to the colour depth of a bitmap image, they measure the same thing in different contexts

effect of sample rate and res

	Sample rate		Sample resolution
	High	Low	High	Low
Playback quality	⇑	⇓	⇑	⇓
File size	⇑	⇓	⇑	⇓

how to calc sound file size

• Sample rate x duration x sample resolution

what is compression

• is reducing the the size of a file so that it takes up less space on secondary storage

• There are scenarios where compression may be needed, such as:

  • Maximise the amount of data you can store on a digital device such as a mobile phone or tablet

  • Minimise the transfer time of data being uploaded, downloaded or streamed across a network such as the Internet

• Compression can be achieved using two methods, lossy and lossless

lossy compression

• Lossy compression is when data is lost in order to reduce the size on secondary storage

• Lossy compression is irreversible

• Lossy can greatly reduce the size of a file but at the expense of losing quality

• Lossy is only suitable for data where reducing quality is acceptable, for example images, video and sound

• In photographs, lossy compression will try to group similar colours together, reducing the amount of colours in the image without compromising the overall quality of the image

lossless compression

• Lossless compression is when data is encoded in order to reduce the size on secondary storage

• Lossless compression is reversible, the file can be returned to its original state

• Lossless can reduce the size of a file but not as dramatically as lossy

• Lossless can be used on all data but is more suitable for data where a loss in quality is unacceptable, for example documents

• In a document, lossless compression uses algorithms to analyse the contents looking for patterns and repetition. For example, repeating characters are replaced with a single character and the number of occurrences in the document (“EEEEE” becomes “E5”)

what is huffman coding

• is a method of lossless compression primarily used on text based data (documents)

• A huffman coding tree is used to compress the data whilst keeping all the data so that it can be uncompressed back to its original state

what is a huffman tree

• A huffman tree, also known a binary tree is used to lossless compress text based data as part of huffman coding

  • A huffman tree consists of nodes which can have either 0, 1 or 2 child nodes

how to draw a huffman tree (brief)

list frequencies, highest going on the top, 0,1 and then go down in frequency coming off the previous node.

what is run length encoding

is a form of data compression that condenses identical elements into a single value with a count

rle text files

• For a text file containing the string "AAAABBBCCDAA", the plain RLE encoding would be "4A3B2C1D2A"

• The string has:

  • four 'A's (4A)

  • three 'B's (3B)

  • two 'C's (2C)

  • one 'D' (1D)

  • two 'A's (2A)

• To represent this in binary, the count is stored in a fixed size binary format (e.g. 7 or 8 bits)

• The character is stored using its ASCII value (7 bits)

• The binary RLE representation of 4A would be 0000100 1000001

  • 0000100 - binary for the count (4)

  • 1000001 - binary for 'A' (65)

rle images

• In bitmap images, RLE is used to compress sequences of the same colour

• For example, a line in an image with 5 red pixels followed by 3 blue pixels could be represented as "5R3B"

• The image has:

  • 5 red pixels (5R)

  • 3 blue pixels (3B)

• To represent this in binary, the pixel count is stored in a fixed size binary format (e.g. 1, 4, 8 or 16 bits)

• The colour is stored based on the required colour depth of the image

• For this example we will assume a colour depth of 2 bits

  • 00 - Black

  • 01 - Red

  • 10 - Green

  • 11 - Blue

• The binary representation of 5R3B would be 1001 01 0011 11

  • 1001 - pixel count (5), 01 - red

  • 0011 - pixel count (3), 11 - blue