Partial Fourier, Non-Cartesian, 3D k-Space, Compressed Sensing (9.6.1 - 9.6.4)

What determines the total time to acquire an MRI image?

The total time to acquire an MRI image is determined by how long it takes to sufficiently sample k-space. This is affected by the need to limit the sampling time to minimize transverse relaxation (T2 decay) during readout.

What is the Partial Fourier method in MRI, and how does it work?

The Partial Fourier method reduces the number of k-space samples needed by taking advantage of k-space symmetries for real-valued images. It collects only half of the k-space data, such as the lines of positive k_y , and uses the symmetry to reconstruct the rest. This reduces acquisition time.

What limitations does Partial Fourier face, and how are they addressed?

Partial Fourier works best when there are minimal errors in the data. To address potential errors, a slightly larger fraction of k-space is often collected, especially around the center, to improve error correction and reconstruction quality.

What is a Non-Cartesian k-space trajectory?

A Non-Cartesian k-space trajectory refers to sampling paths that do not follow a standard grid pattern (Cartesian). These paths can include spiral or radial (spoke-like) designs instead of straight lines.

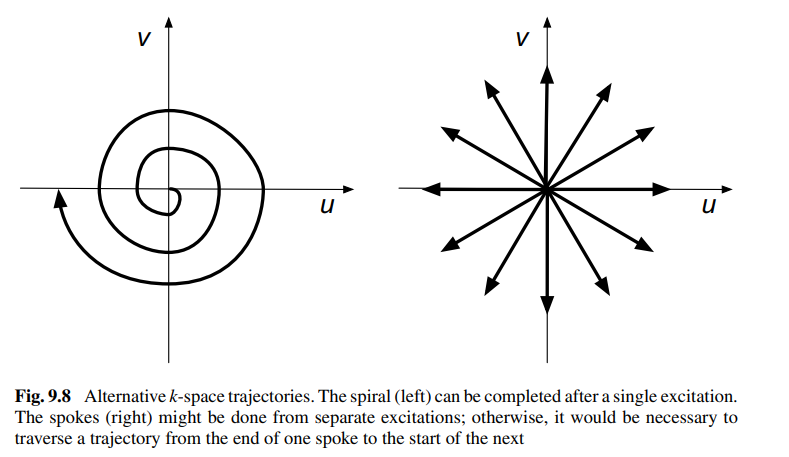
What are the benefits and challenges of using Non-Cartesian trajectories in MRI?

Benefits:

- Lower sensitivity to motion artifacts compared to Cartesian trajectories.

Challenges:

- Non-Cartesian data must be resampled onto an even grid for efficient Fourier transformation. This requires additional computation and can complicate the reconstruction process.

What is the advantage of acquiring a 3D k-space over a slice-by-slice method in MRI?

Acquiring a 3D k-space allows for exciting a much larger volume of tissue in a single excitation, which increases the Signal-to-Noise Ratio (SNR) because more hydrogen nuclei contribute to the measured signal.

What is the major disadvantage of acquiring a 3D k-space compared to a 2D slice-by-slice approach?

Acquiring a 3D k-space takes longer to traverse due to the need to sample all the dimensions of the volume. This extended time increases T₂ decay effects, which can reduce the resolution of the image. The Point Spread Function (PSF) of 3D imaging is often poorer than that of multi-slice 2D imaging.

What does compressed sensing in MRI rely on?

Compressed sensing relies on the fact that most images contain redundant information. This allows for reconstructing an image even if not all k-space data is collected, by using specific reconstruction algorithms instead of standard Fourier transforms.

Why can't standard Fourier reconstruction be used for compressed sensing?

Standard Fourier reconstruction assumes complete or Nyquist-sampled k-space data. Compressed sensing collects data in a way that violates these assumptions, requiring alternative reconstruction methods.

How does compressed sensing work to reconstruct images from under-sampled k-space data?

Compressed sensing uses constraints based on known image properties, such as sparsity. It applies a "sparsifying transform," which leverages features like finite differences to represent images compactly, helping distinguish signals from random noise.

Why are random sampling patterns used in compressed sensing?

Random sampling reduces coherent artifacts in the reconstructed image, making the missing data appear as noise rather than structured distortion.

What is an example of a constraint used in compressed sensing reconstruction?

An example is the sparsity of angiographic images, where most voxels are either background or vessels. This property is used to apply sparsifying transforms for reconstruction.

Why is fully random sampling of k-space difficult in practice?

Frequency and phase encoding in MRI require structured paths through k-space, making true random sampling challenging. However, compressed sensing principles can still be applied to under-sampled data within these constraints.