1.07 Ratio & Proportion
0.0(0)
0.0(0)
Card Sorting
1/14
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
15 Terms
1
New cards
Ratio
Way of comparing 2 or more numbers a and b in the form of a : b (such that b is not 0) to show the relationship between their values.
Ratios can be contain 3, i.e. 3-way ratios (e.g: a:b:c), or more numbers/variables, they don’t have to only contain 2 numbers.
Ratios can be contain 3, i.e. 3-way ratios (e.g: a:b:c), or more numbers/variables, they don’t have to only contain 2 numbers.
2
New cards
Ratio notation
Separate the compared values with a colon (:)
E.g: The ratio of a to b to c can be written as a : b : c
E.g: The ratio of a to b to c can be written as a : b : c
3
New cards
Is the ratio a:b the same as the fraction a/b?
NO!!!
A ratio is a **comparison between the 2 or more values**, while a fraction is a **mathematical expression showing parts of a whole**.
The ratio a:b means that a is a/b of b (a/b \* b = a) or that b is b/a of a (b/a \* a = b).
The fraction a/b means a/b of the **whole** quantity (i.e. b, the denominator, is considered the **entire** quantity, whereas a is simply compared to that entire total quantity). This is DIFFERENT from ratios, because the total for ratios would be **a + b**, **NOT** just b.
A ratio is a **comparison between the 2 or more values**, while a fraction is a **mathematical expression showing parts of a whole**.
The ratio a:b means that a is a/b of b (a/b \* b = a) or that b is b/a of a (b/a \* a = b).
The fraction a/b means a/b of the **whole** quantity (i.e. b, the denominator, is considered the **entire** quantity, whereas a is simply compared to that entire total quantity). This is DIFFERENT from ratios, because the total for ratios would be **a + b**, **NOT** just b.
4
New cards
How do you simplify ratios?
Simplifying ratios works the same way as we simplify fractions (because we’re just cancelling out common factors). BUT be wary that ratios and fractions ARE NOT necessarily interconvertible in all situations.
E.g: 8:6 can be simplified to 4:3 just as 8/6 = (8/2)/(6/2) = 4/3 where 2 is the common factor.
E.g: 8:6 can be simplified to 4:3 just as 8/6 = (8/2)/(6/2) = 4/3 where 2 is the common factor.
5
New cards
How do you divide a quantity c into a ratio a:b ?
a = a/(a+b) of the whole quantity c → a = a/(a+b) \* c = ac/(a+b)
b = b/(a+b) of the whole quantity c → b = b/(a+b) \* c = bc/(a+b)
b = b/(a+b) of the whole quantity c → b = b/(a+b) \* c = bc/(a+b)
6
New cards
How do you find the simplest 3-way ratio a:b:c when given a:b and b:c?
1. Find the LCM of the value of b in the ratio a:b and the value of b in the ratio b:c. Finding the LCM allows the 3-way ratio a:b:c that we find in the end to be in its simplest form (but we can always double check this where necessary).
2. Multiply the ratios a:b and b:c by their relevant, respective scale factors so that b is equal to the LCM in both ratios.
3. Now simply combine the 3 numbers from step 2 to get the 3-way ratio a:b:c.
Example: Given that a:b is 5:6 and b:c is 9:10, find the ratio a:b:c.
1. LCM of b’s value in a:b and b’s value in b:c is LCM(6,9) = 18
2. 18/6 = 3 → scale factor to multiply ratio of 5:6 by is 3 → a:b should be 5x3 : 6x3 = 15 : 18
18/9 = 2 → scale factor to multiply ratio of 9:10 by is 2 → b:c should be 9x2 : 10x2 = 18 : 20
3. Ratio a:b:c = 15:18:20
7
New cards
Direct proportionality definition
2 variables have a constant ratio;
As 1 variable increases, the other variable increases at the same rate. As 1 variable decreases, the other variable decreases at the same rate. (THIS ONLY APPLIES WHEN THE CHANGE IS THROUGH MULTIPLYING OR DIVIDING):
As 1 variable is increased (multiplied) by a scale factor, the other variable is increased (multiplied) by that same scale factor.
As 1 variable is decreased (divided) by a scale factor, the other variable is decreased (divided) by that same scale factor.
As 1 variable increases, the other variable increases at the same rate. As 1 variable decreases, the other variable decreases at the same rate. (THIS ONLY APPLIES WHEN THE CHANGE IS THROUGH MULTIPLYING OR DIVIDING):
As 1 variable is increased (multiplied) by a scale factor, the other variable is increased (multiplied) by that same scale factor.
As 1 variable is decreased (divided) by a scale factor, the other variable is decreased (divided) by that same scale factor.
8
New cards
Direct proportionality notation and formula
Notation: y ∝ x
Formula: y = kx, where k is the constant of proportionality.
* y/x = k (k is constant → constant ratio)
Formula: y = kx, where k is the constant of proportionality.
* y/x = k (k is constant → constant ratio)
9
New cards
Direct proportionality graph
Linear graph (straight line) that goes through the origin (0,0).
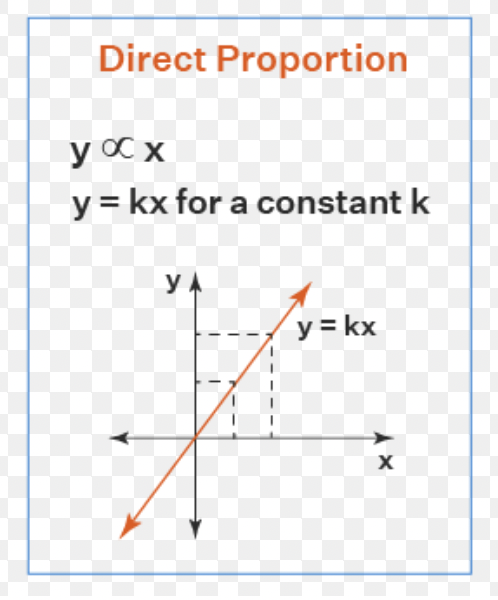
10
New cards
Inverse proportionality definition
2 variables have a constant product;
As 1 variable decreases, the other variable increases at the same rate. As 1 variable increases, the other variable decreases at the same rate. (THIS ONLY APPLIES WHEN THE CHANGE IS THROUGH MULTIPLYING OR DIVIDING):
As 1 variable is increased (multiplied) by a scale factor, the other variable is decreased (divided) by that same scale factor.
As 1 variable is decreased (divided) by a scale factor, the other variable is increased (multiplied) by that same scale factor.
As 1 variable decreases, the other variable increases at the same rate. As 1 variable increases, the other variable decreases at the same rate. (THIS ONLY APPLIES WHEN THE CHANGE IS THROUGH MULTIPLYING OR DIVIDING):
As 1 variable is increased (multiplied) by a scale factor, the other variable is decreased (divided) by that same scale factor.
As 1 variable is decreased (divided) by a scale factor, the other variable is increased (multiplied) by that same scale factor.
11
New cards
Inverse proportionality notation and formula
Notation: y ∝ 1/x
Formula: y = k/x, where k is the constant of proportionality.
* xy = k (k is constant → constant product)
Formula: y = k/x, where k is the constant of proportionality.
* xy = k (k is constant → constant product)
12
New cards
Inverse proportionality graph
Downward-sloping curved graph (reciprocal graph), it does not touch any of the axes.

13
New cards
Constant of proportionality
The constant of proportionality is k in y = k/x or y = kx, it is the constant value that does not change and which determines how 2 variables are inversely or directly related to one another.
14
New cards
How to use direct or inverse proportionality to find unknown quantities?
1. Identify whether the problem involves direct or inverse proportionality.
2. Write the relevant formula:
1. y = kx if direct proportion is involved
2. y = k/x if inverse proportion is involved
3. Substitute in the relevant values for x and/or y given in the equation, then calculate k.
4. Once you have found k, rewrite the entire formula y= kx or y = k/x but instead of k write the value you found.
5. Now substitute the value of x or y given into the formula found in step 4 and calculate the value of y or x you need to find.
Example: 6 workers take 12 days to finish a task. How many days will 8 workers take to finish that same task?
More workers → less time needed to finish task
Less workers → more time needed to finish task
Number of workers is inversely proportional to time taken to finish task
Let number of workers = N and time taken to finish task (days) = D
N = k/D
Substituting (N,D) = (6,12) we have:
6 = k/12
k = 72
N = 72/D
We now have 8 workers, how many days does it take? Substituting N = 8 we get:
8 = 72/D
8D = 72
D = **9 days**
15
New cards
How do you solve problems about ratio and proportion for maps and scale diagrams?
Let the distance on the map be M, the distance in real life be R, and the distance you want to find be F.
Scale factor ratio = M : R
1. To find a distance F (in real life) represented by distance of B on the map when you are given the scale factor M : R, calculate:
1. F = B x (R/M)
2. E.g: A map has a scale factor of 1 : 1000, how many kilometers in real life does a distance of 18cm on the map depict?
F = 18 x (1000/1) = 18000cm = 180m = **0.18km**
2. To find a distance F (on the map) representing the distance of B in real life when you are given the scale factor M : R, calculate:
1. F = B x (M/R)
2. E.g: A map has a scale factor of 1 : 1000, how many cm on the map depicts a distance of 0.45 kilometers in real life?
0\.45 km = 450m = 45000cm
F = 45000 x (1/1000) = **45cm**
Direct proportion: R = kM
1. Substitute values for R and M into formula to find k.
2. Write formula again except replace k with the value found in step 1.
3. Substitute the value for R or M into the formula found in step 2 then find the relevant value for M or R.
4. E.g: a distance of 900cm in real life is depicted by a distance of 1cm on the map, what does a distance of 45cm on the map depict in real life?
1. Method 1:
2. R = kM → 900 = k(1) → k = 900
3. R = 900M
4. R = 900(45) = **40500cm**
5. Method 2:
6. 900/1 = x/45
7. x = 45(900) = **40500cm**
Scale factor ratio = M : R
1. To find a distance F (in real life) represented by distance of B on the map when you are given the scale factor M : R, calculate:
1. F = B x (R/M)
2. E.g: A map has a scale factor of 1 : 1000, how many kilometers in real life does a distance of 18cm on the map depict?
F = 18 x (1000/1) = 18000cm = 180m = **0.18km**
2. To find a distance F (on the map) representing the distance of B in real life when you are given the scale factor M : R, calculate:
1. F = B x (M/R)
2. E.g: A map has a scale factor of 1 : 1000, how many cm on the map depicts a distance of 0.45 kilometers in real life?
0\.45 km = 450m = 45000cm
F = 45000 x (1/1000) = **45cm**
Direct proportion: R = kM
1. Substitute values for R and M into formula to find k.
2. Write formula again except replace k with the value found in step 1.
3. Substitute the value for R or M into the formula found in step 2 then find the relevant value for M or R.
4. E.g: a distance of 900cm in real life is depicted by a distance of 1cm on the map, what does a distance of 45cm on the map depict in real life?
1. Method 1:
2. R = kM → 900 = k(1) → k = 900
3. R = 900M
4. R = 900(45) = **40500cm**
5. Method 2:
6. 900/1 = x/45
7. x = 45(900) = **40500cm**