Derivatives Formulas

Basic Differentiation Rules for Elementary Functions

3.1 Chain Rule

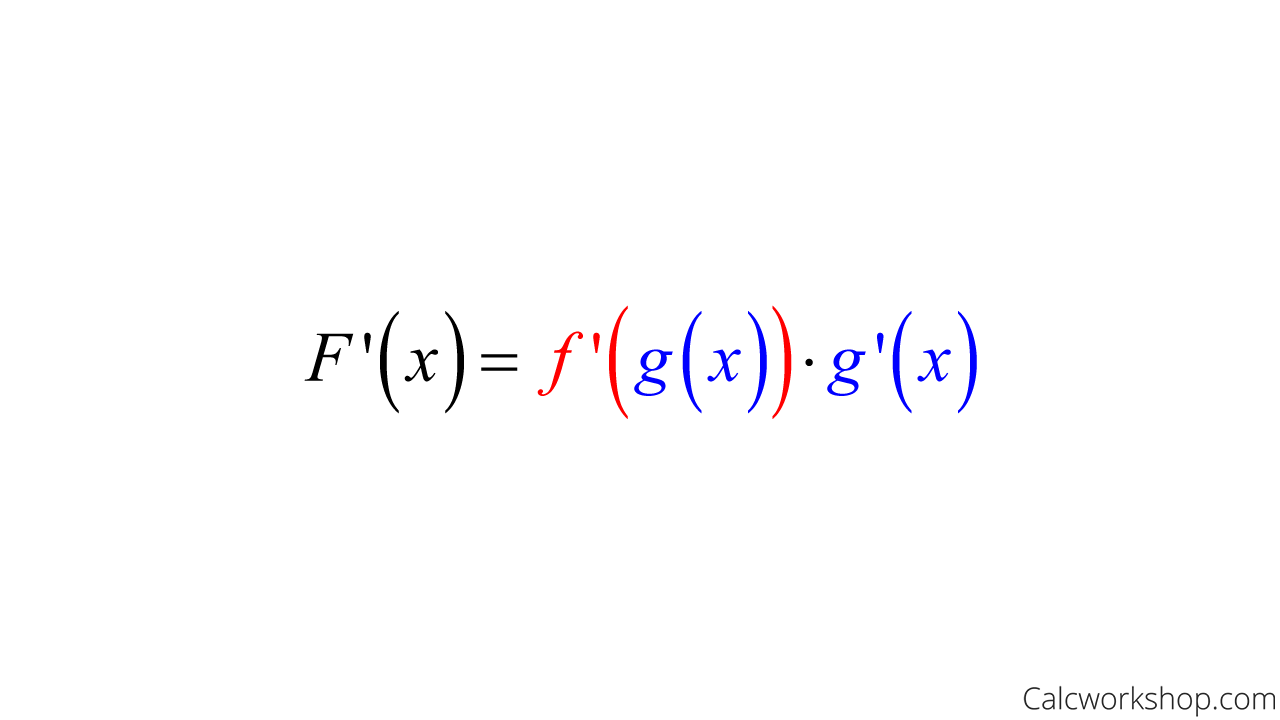
d/dx sin u(x)

cos u(x) du/dx

d/dx cos u(x)

-sin u(x) du/dx

d/dx tan u(x)

sec^2 u(x) du/dx

d/dx sec u(x)

sec u(x) tan u(x) du/dx

d/dx csc u(x)

-csc u(x) cot u(x) du/dx

d/dx cot u(x)

-csc^2 u(x) du/dx

General Power Rule

d/dx [u^n]

n[u(x)]^n-1 du/dx

Exponential Function to Base a

a^x

e^(ln a * x)

Derivative of y=a^x

d/dx [a^x]

(ln a) a^x

d/dx [a^u]

(ln a) a^u du/dx

Implicit Form

It is inconvenient or impossible to write explicit. Ex: xy=1

Explicit Form

y is explicitly written as a function of x, y=f(x)

Example: y=1/x=x^-1

3.3 Derivatives of an Inverse Trigonometric Function

d/dx [arc sin u] OR sin^-1 (u)

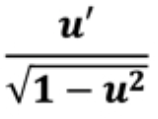
d/dx [arc tan u]

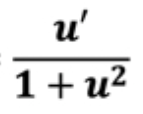
d/dx [arc cos u]

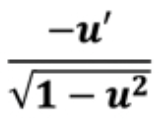
d/dx [arc cot u]

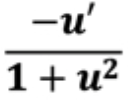
d/dx [arc sec u]

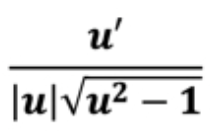
d/dx [arc csc u]

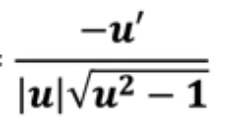
3.4 Derivative of a Logarithmic Function

d/dx [log a x]

1 / (ln a) x

d/dx [log a u]

1 / (ln a) u du/dx = u’ / u*ln a

d/dx [ln x]

1/x

d/dx [ln u]

u’/u

Theorem: The Number e as a Limit

d/dx [u + v]

du/dx + dv/dx

d/dx [fg]

f’g + fg’

d/dx [f/g]

(f’g - fg’) / g²

d/dx [e^u]

c^u * u’

d/dx [1/g(x)]

g’(x) / (g(x))²

d/dx [ |u| ]

u / |u| * u’