Lec 12 descriptive stats II

2 most common ways to summarize data

• Central tendency and measures of variability

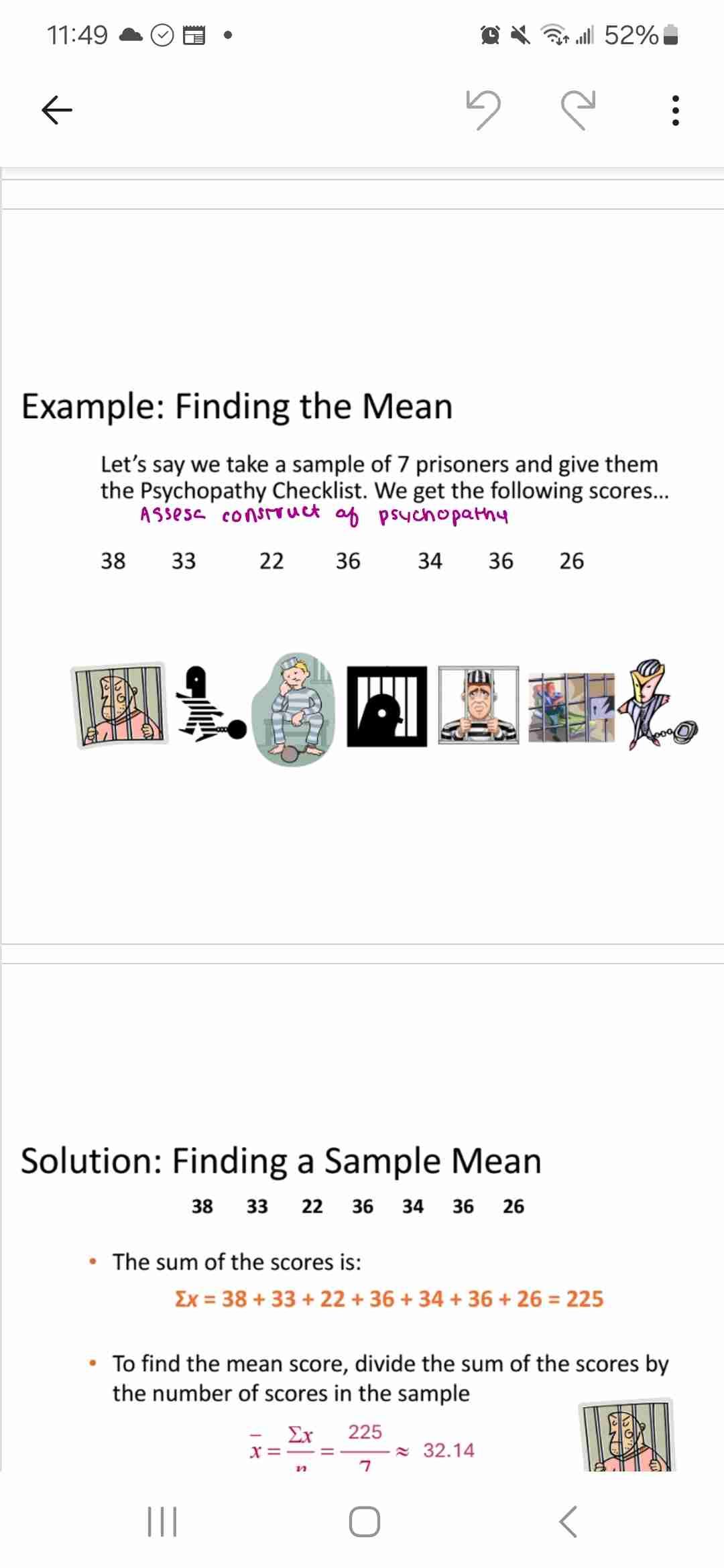
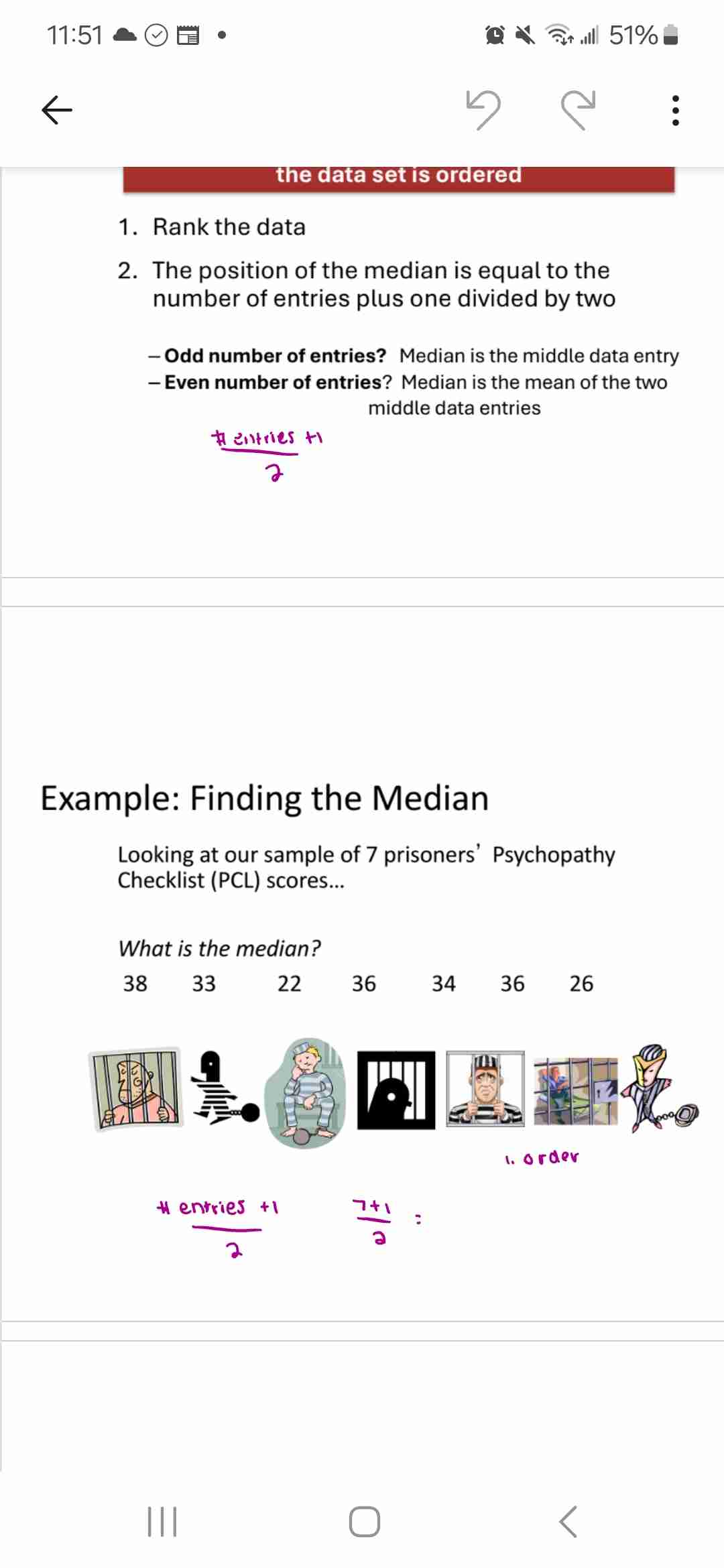
Median

• Value in center of data when ordered

• (No of entries +1)/2

  • If even no of entries, use mean of 2 enter ones

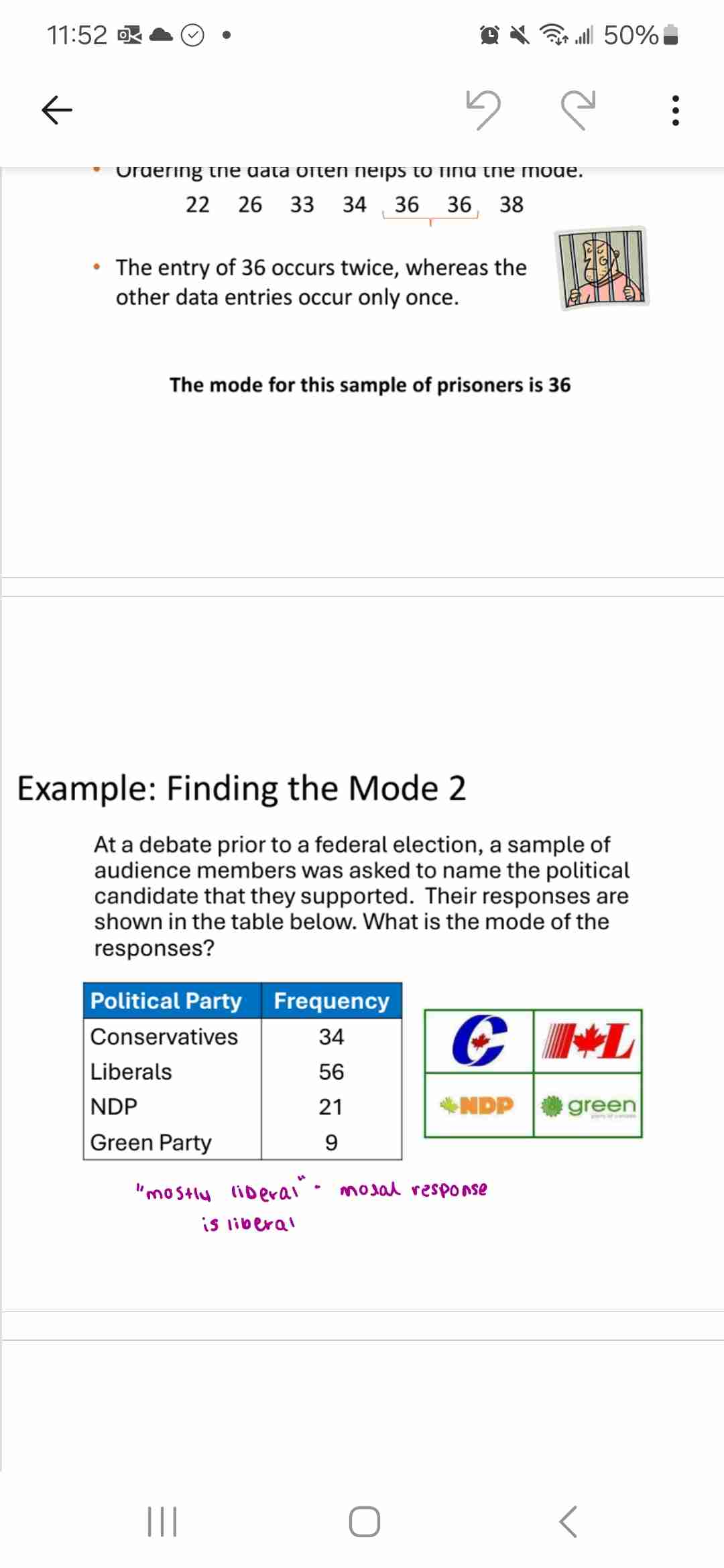
Mode

Most frequent value

• If none repeat, 0 mode

Dis/advantages of mean

• +: common, account for every data set

• - : affected by extreme scores and lose indiv data

Dis/advantages of median

+: little influence by extreme scores, realistic middle score

-: maybe bad to ignore extreme data

Dis/advantages of mode

+: freq obtained, not affected by extreme scores

-: may not rep whole of scores, ignore extreme data

Measures of variability and inclusions

• How spread out data is

  • Range (iqr)

  • Deviation

  • Variance

  • Sd

Range

Biggest to smallest scores

Sensitive to

• Sample size (smaller, less range)

  • Extreme scores

Inter quartile range

• Dist btw 1st and 3rd quartile

• Include just the middle 50% of values q3-q1

• Positive: not affected by extremes

• Median: 2nd quartile

• 75% scores fall above 1st quart, 25% below

Iqr and outliers

Finding with iqr:

• Scores > q3 + (1.5xIQR) are high end outliers . Anything outside this is outlier

• Scores <Q1 + 1.5xIQR) are low end outliers

Box and whisker plot

• How does it improve on iqr

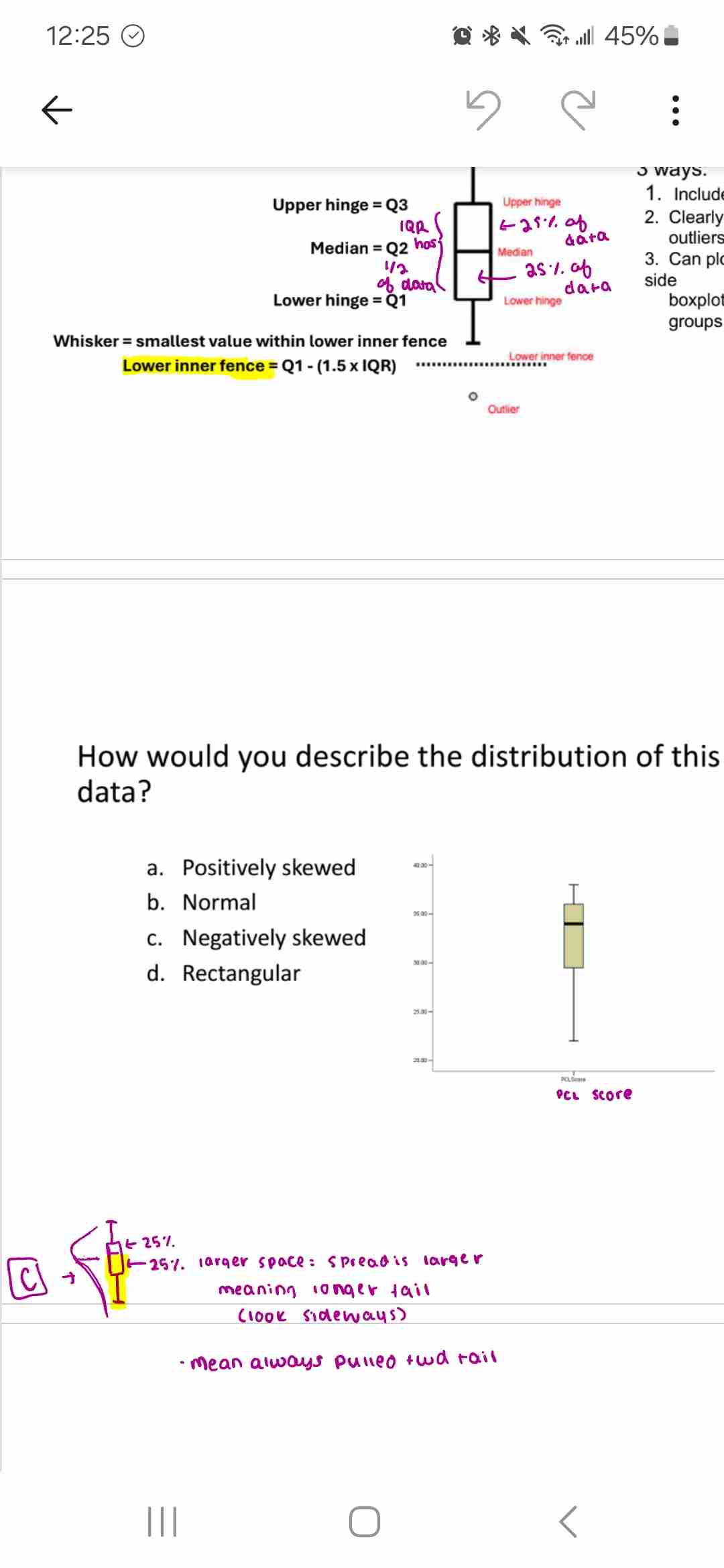
C

Deviation (variability measure)

Pop and sample dev

Diff btw each score and mean of data set

D

Variance and sum of squares

Single no representing avg amount of variation in set of scores

• Sample variance: s² (n-1 otherwise underestimate variance efgect)

• Population variance: o²

Steps to get sample variance

Standard deviation

• Measure of score spread out from mean

• Calculate variance the sqrt

Interpreting sd

• More spread out data = higher sd