Chapter 5: Newton's Laws of Motion

These flashcards cover key vocabulary terms and concepts related to Newton's Laws of Motion and their applications, including forces, laws of motion, energy, and work.

Field Forces

• no physical contact

• Strong Force

• Electromagnetic Force

• Weak Force

• Gravitational Force

Strong Force

• within nucleus that holds protons

• 10^-15 m

Electromagnetic Force

• between charges → made us

• aware of interactions such as attraction and repulsion. The electromagnetic force is responsible for electricity, magnetism, and light.

Weak Force

• radioactive processes → nuclear reaction in sun

• 10^-15 m

Gravitational Force

• between masses

• weakest of all

Newton's First Law of Motion

• an object moves with a constant speed in a straight line unless a non-zero net force acts on it

  • moves with velocity constant in magnitude and direction

Net Force

The vector sum of all external forces exerted on an object

Newton’s First Law: air hockey puck example

• without air, there’s friction

• when friction is removed by air, it moves in a straight line at a constant speed until collision with another object

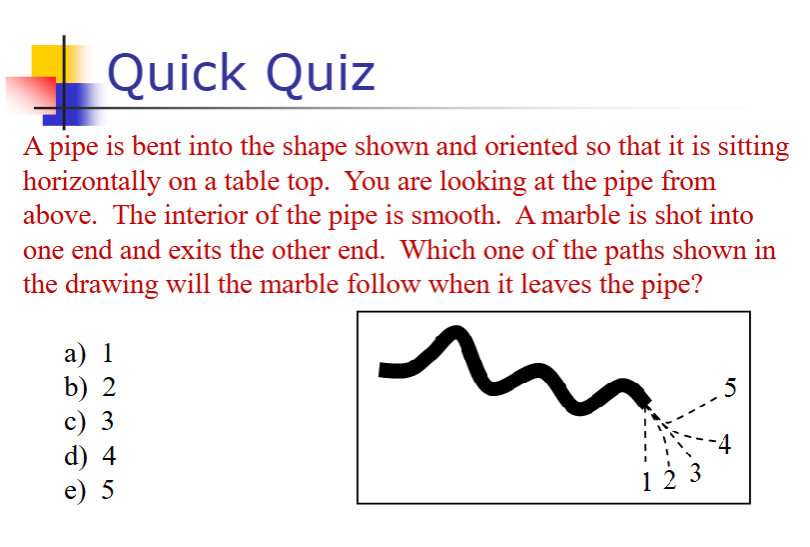
3 - in a straight line

Newton's Second Law of Motion

The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma)

• F & a are both vectors

Units of Force

The SI unit of force is the Newton (N), which is defined as the force required to accelerate a one-kilogram mass by one meter per second squared.

• 1 N = 1 (kg*m)/s²

US Customary unit of force is a pound (lb): 1 N = 0.225 lb

Which describes net force?

The quantity that changes the velocity of an object

Free Fall

The motion of a body when only the force of gravity is acting on it, with no air resistance.

• F = ma

  • a = 9.8 m/s² → always constant

• C = 2πr

  • C/d = C/2r = π

In a free fall, the greater the mass of the object…

• the greater its force of attraction toward the earth

• the smaller its tendency to move (the greater its inertia)

If F = 10, and m = 1 kg in a free fall, what is a?

• F = ma

• a = F/m = 10 N/1 kg = 10 m/s²

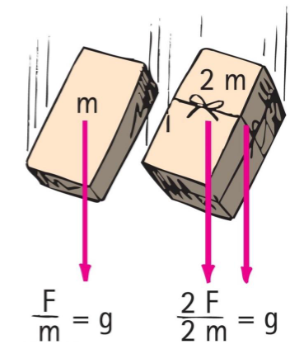
What explains why freely falling objects of various masses have the same accelerations?

• Newton’s second Law

• F/m = g, 2F/2m = g

Weight

• W = mg

• special case of Newton’s 2nd Law where a = g = 9.8 m/s² due to gravity

• Unit: N or lb (not kg)

kinematic equations: 

• v = v₀+at

• Δx = v₀t + ½ at²

• v² = v₀² + 2aΔx

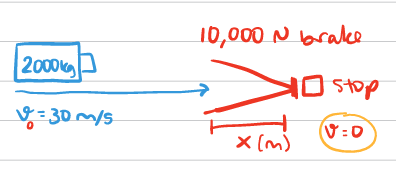
• F = ma

• 10,000 N = 2,000 kg (a)

• a = 5 m/s²

• Use kinematic equation: v² = v₀² + 2aΔx

  • 0² = (30 m/s)² + 2(5)Δx

  • (-30 m/s)² = 10Δx

  • Δx = 900/10 = 90 m

Newton’s Third Law of Motion

• if object 1 & object 2 interact, the force exerted by object 1 on object 2 will be equal in magnitude but opposite in direction

  • action forces = (-)reaction forces

  • action: tire pushes on road, reaction: road pushes on tire

  • action: rocket pushes on gas, reaction: gas pushes on rocket

Action: earth pulls apple down, reaction: apple pulls earth up?

Yes, just not strong enough (mass apple = 1, earth = 10^(24))

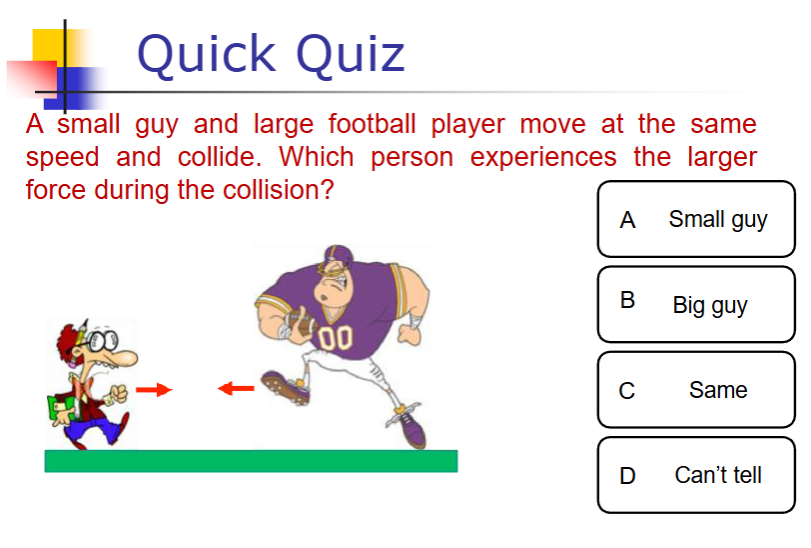
C: same

• F will be equal & opposite, a will be different

Newton’s 2nd Law in Component Form

• ∑F_x = ma_x

• ∑F_y = ma_y

• a = sqrt( a_x² + a_y²); F = sqrt( F_x² + F_y²)

According to Newton’s Second Law (Component Form), an object either at rest or with a constant velocity is…

• at equilibrium

• ∑F = 0 because a = 0 when v = 0 or v = constant

  • net force acting on it is 0 because a = 0

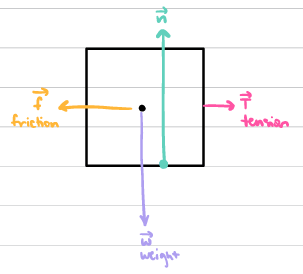
Normal Force

The perpendicular force exerted by a surface to support the weight of an object resting on it.

• example: force table exerts on tv

• n’ is the reaction: the tv on the table

• n = -n’

Tension

• The force transmitted through a string, rope, or cable/cord when it is pulled tight by forces acting from opposite ends.

• Cord is attached to a body and pulls on the body with a force T directed away from the body of mass and along the cord

• The forces at the two ends of the cord are equal in magnitude

Friction

• The force that opposes the motion of an object when it is in contact with a surface.

• always in opposite direction to F (F is force applied)

Free Body Diagram

• identifying all forces acting on an object

  • ∑F_x = ma_x

  • ∑F_y = ma_y

• masses of strings or ropes are negligible

Weighing Machine

• A device used to measure weight by balancing the gravitational force on an object against a known reference force, typically using springs or load cells.

• measures normal force

• ∑F_y = ma_y

• n↑ (normal force) & w↓ (weight)

  • n - w = 0

  • n = w = mg

If the mass of a person on a weighing machine is 70 kg, what is the normal force exerted?

• n = w = mg

• n = 70 kg * 9.8 m/s² = 686 N (upward)

• there is no horizontal (Fx) or acceleration because the person is standing still

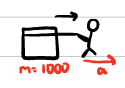
What equations are relevant? If floor is frictional and if it’s not.

• ∑F_x = ma_x

  • F = T 

  • T = ma if floor is not frictional

  • T - f = ma if floor is frictional

• ∑F_y = ma_y

  • no vertical movement, F = 0

  • 0 = n - w

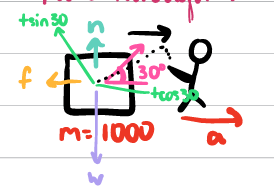
If a person pulls a block (m = 1000 kg) at a 30 degree angle, what expression would you use to find ∑F_x & ∑F_y ?

• ∑F_x = ma_x

  • Tcos(30) - f = F

  • Tcos(30) - f = ma

• ∑F_y = ma_y

  • n + Tsin(30) - w = F

  • no vertical acceleration

  • n + Tsin(30) - w = 0

• ∑F_y = ma_y = 0 BECAUSE they cancel out here

• ∑F_x = ma_x

  • ∑F_x = 2Tcos(35) - f

  • 2Tcos(35) - f = ma_x

  • 2*55 N (cos(35)) - 57 N = 3.7 kg + 19 kg * a

  • a = 1.46 m/s²

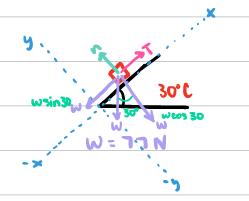
How do you approach an Inclined Planes problem?

• choose coordinate system with x along incline and y perpendicular to incline

• replace force of gravity with its components

• ∑F_x = ma_x

  • Tcos(30) - f = ma

  • write it on the incline:

  • T - wsin(30) = 0

    • weight: n = wcos(30)

    • w = 100 lb - y

    • 100cos(30) = 86.6 lb (we used 77 idk why)

  • T = wsin(30) = 77(1/2) = 38.5 N

• ∑F_y = ma_y 

  • n + Tsin(30) - w = 0

  • n = wcos(30) = 77cos(30) = 66.7 N

1. Before the elevator starts to move:

• spring scale measures normal force (n)

  • Fn = mg = 72 kg * 9.8 m/s² = 720 N = 162 lb

    • 1 N = 0.225 lb

2. During the first 0.80 s of the elevator’s ascent:

• Draw FBD

• ∑F_y = ma_y (only vertical movement)

  • F = n - w = ma

  • n = ma + w

  • n = ma + mg = m(a + g)

    • v = v₀ + at

    • a = (v - v₀)/t = 1.2/0.8 = 1.5 m/s²

  • n = 72 kg (1.5 m/s² + 9.8 m/s²) = 813.6 N

3. When elevator is traveling at a constant speed:

• v = constant

• n = m(g + a) → a = 0

• w = same

• n = mg = 720 N

4. During elevator’s negative acceleration:

• a = (v - v₁)/t = (0 - 1.2)/1.5 = -0.8

• n = m(g + a) = 72 kg (9.8 m/s² - 0.8 m/s²) = 648 N