MATH 226 - Improper Integrals

0.0(0)
studied byStudied by 0 people
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/13

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

14 Terms

1
New cards
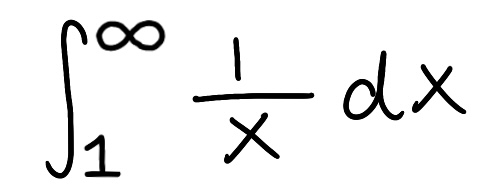
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral diverges because the limit is infinite

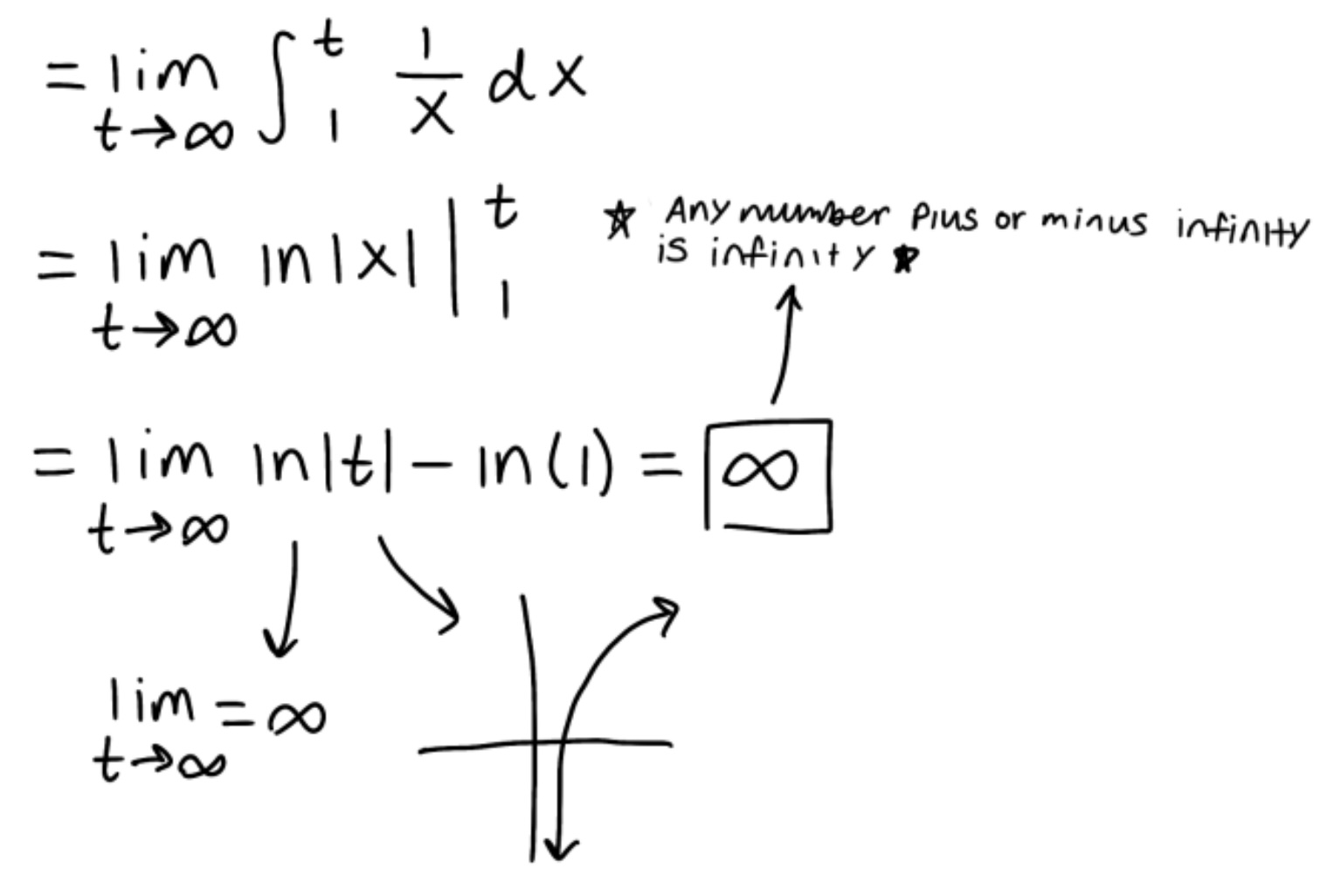
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral diverges because the limit is infinite</p></li></ul><p></p>
2
New cards
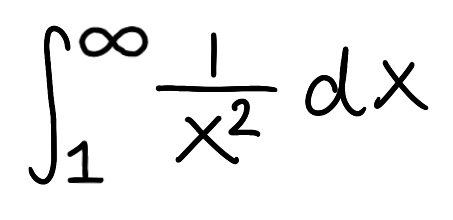
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

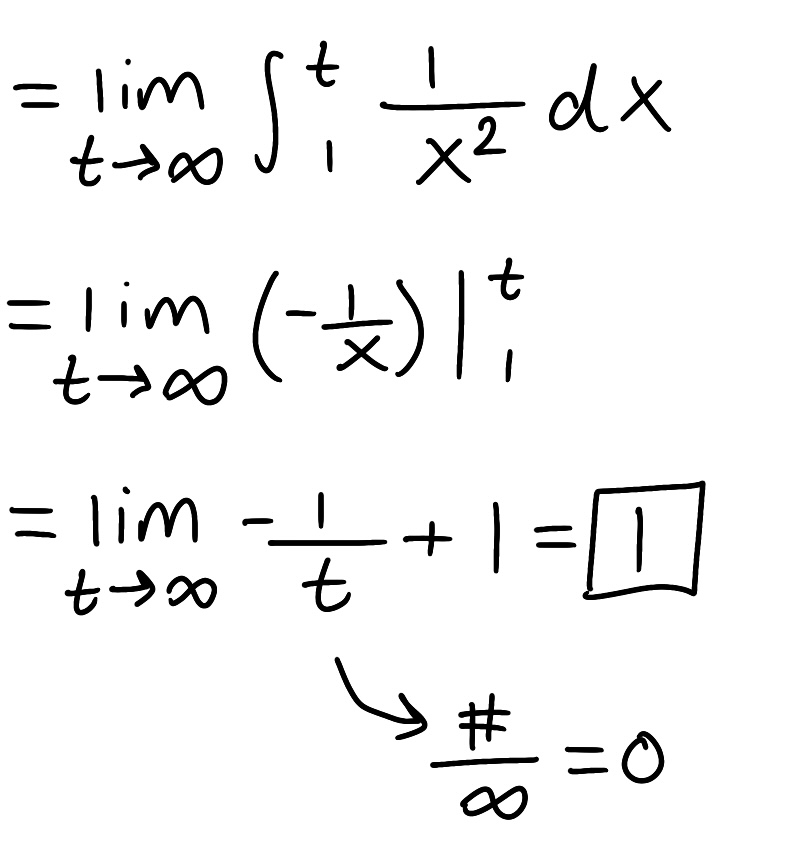
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
3
New cards
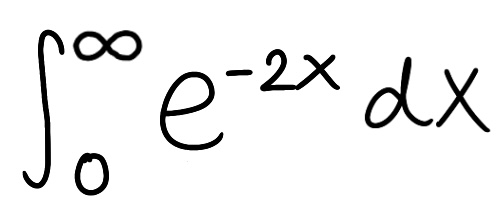
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

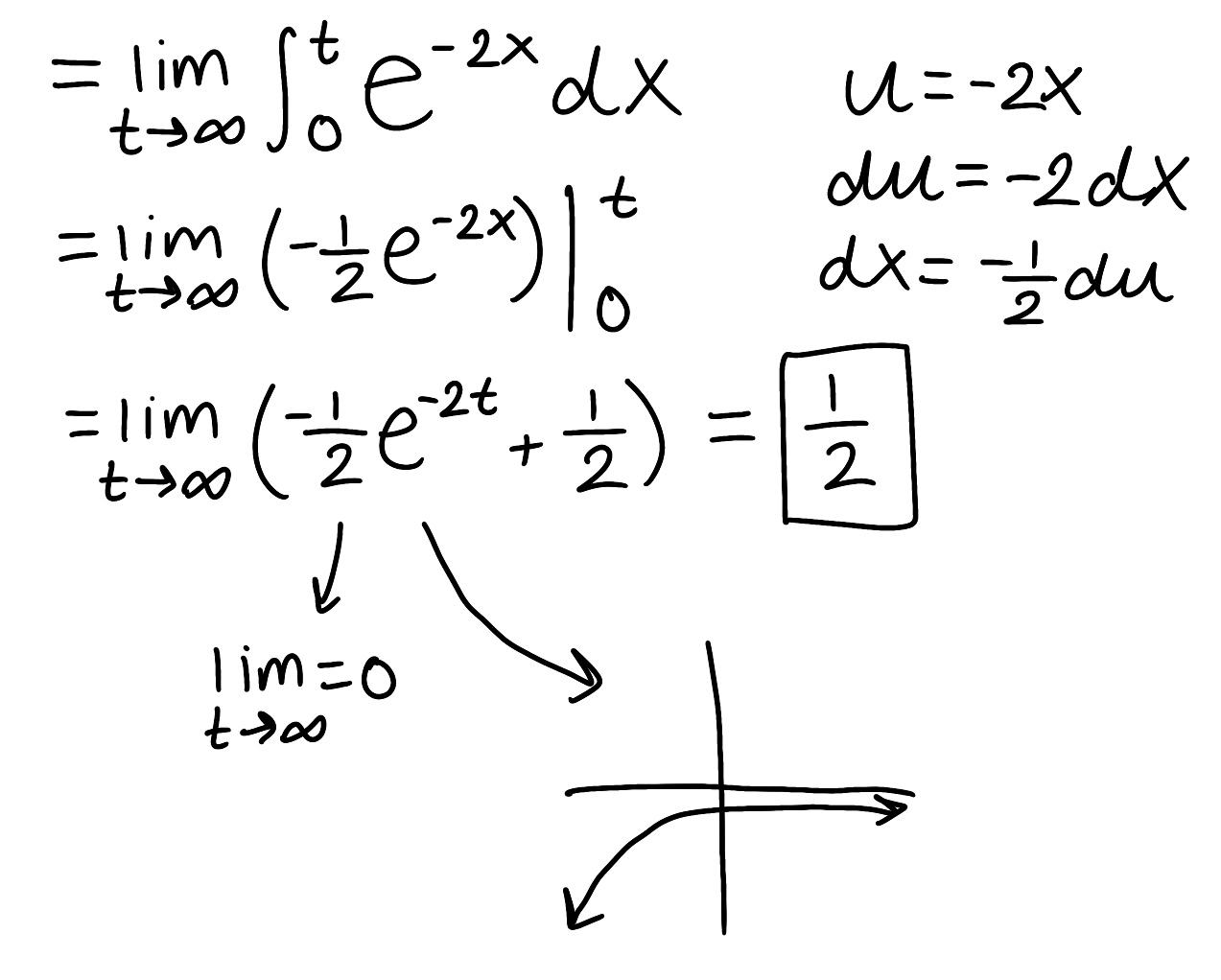
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
4
New cards
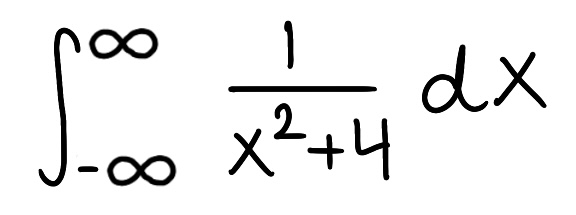
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because both of the bounds are infinite

  • The integral converges because the limit is finite

<ul><li><p>The integral is improper because both of the bounds are infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
5
New cards
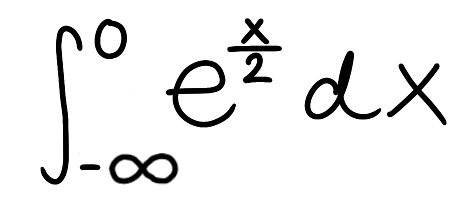
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

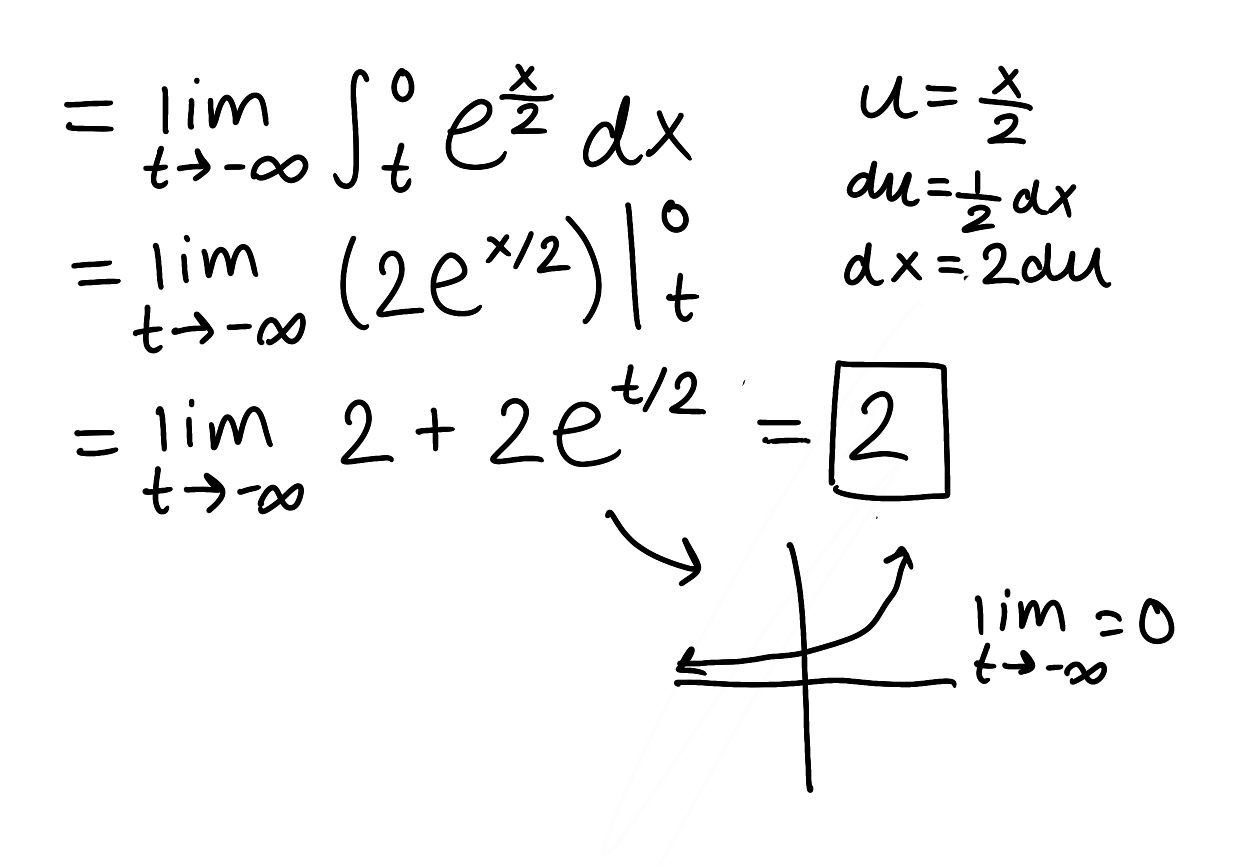
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
6
New cards
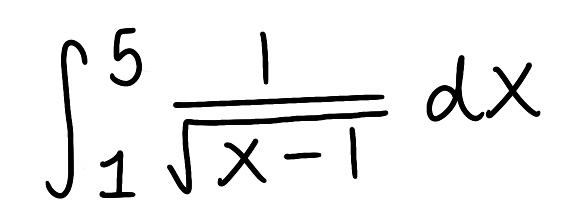
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because there is a discontinuity x=1

  • The integral converges because the limit is finite

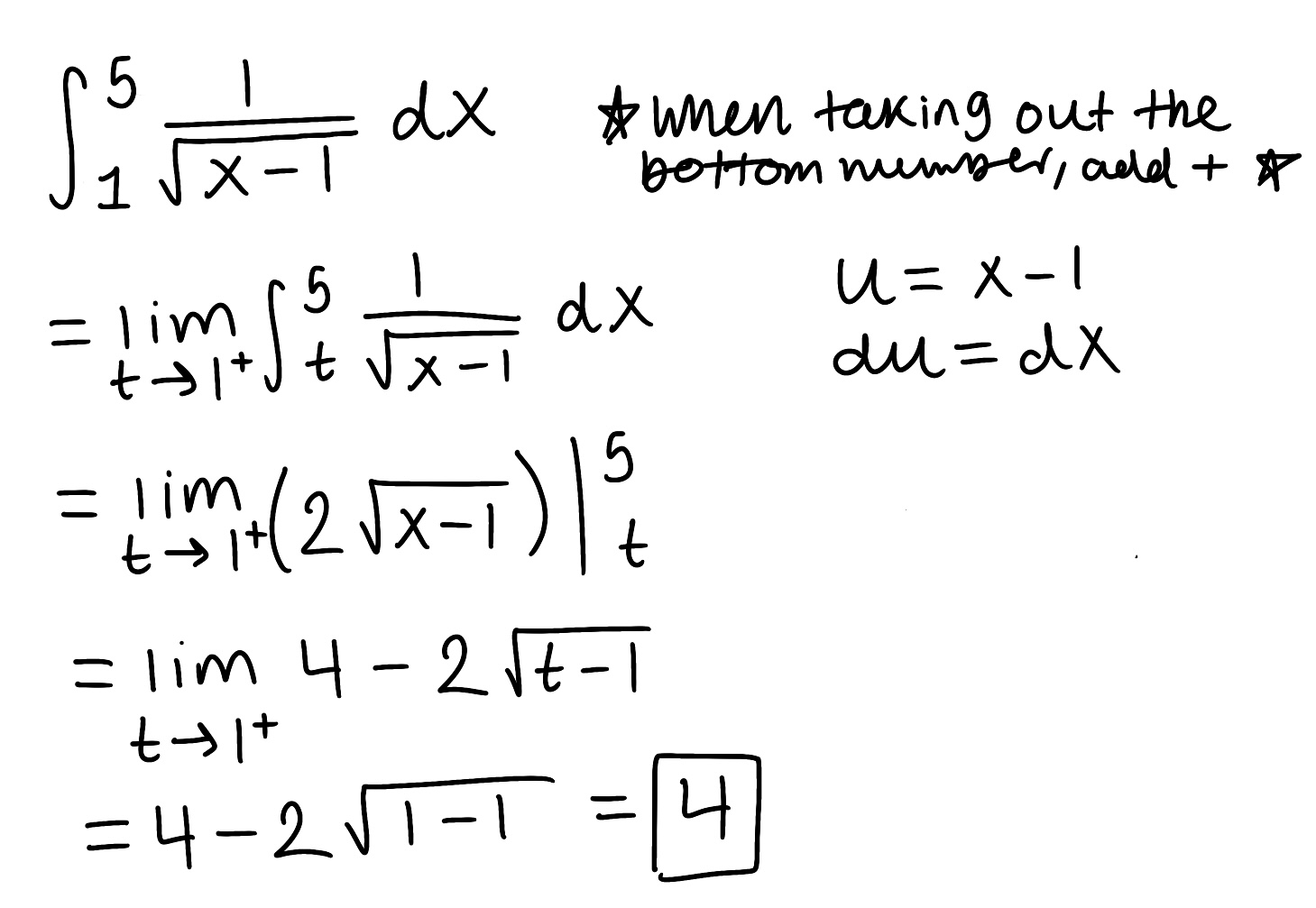
<ul><li><p>The integral is improper because there is a discontinuity x=1 </p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
7
New cards
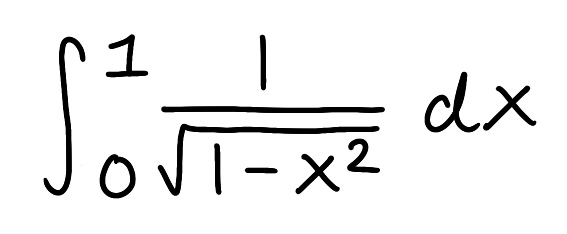
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because there is a discontinuity x=1

  • The integral converges because the limit is finite

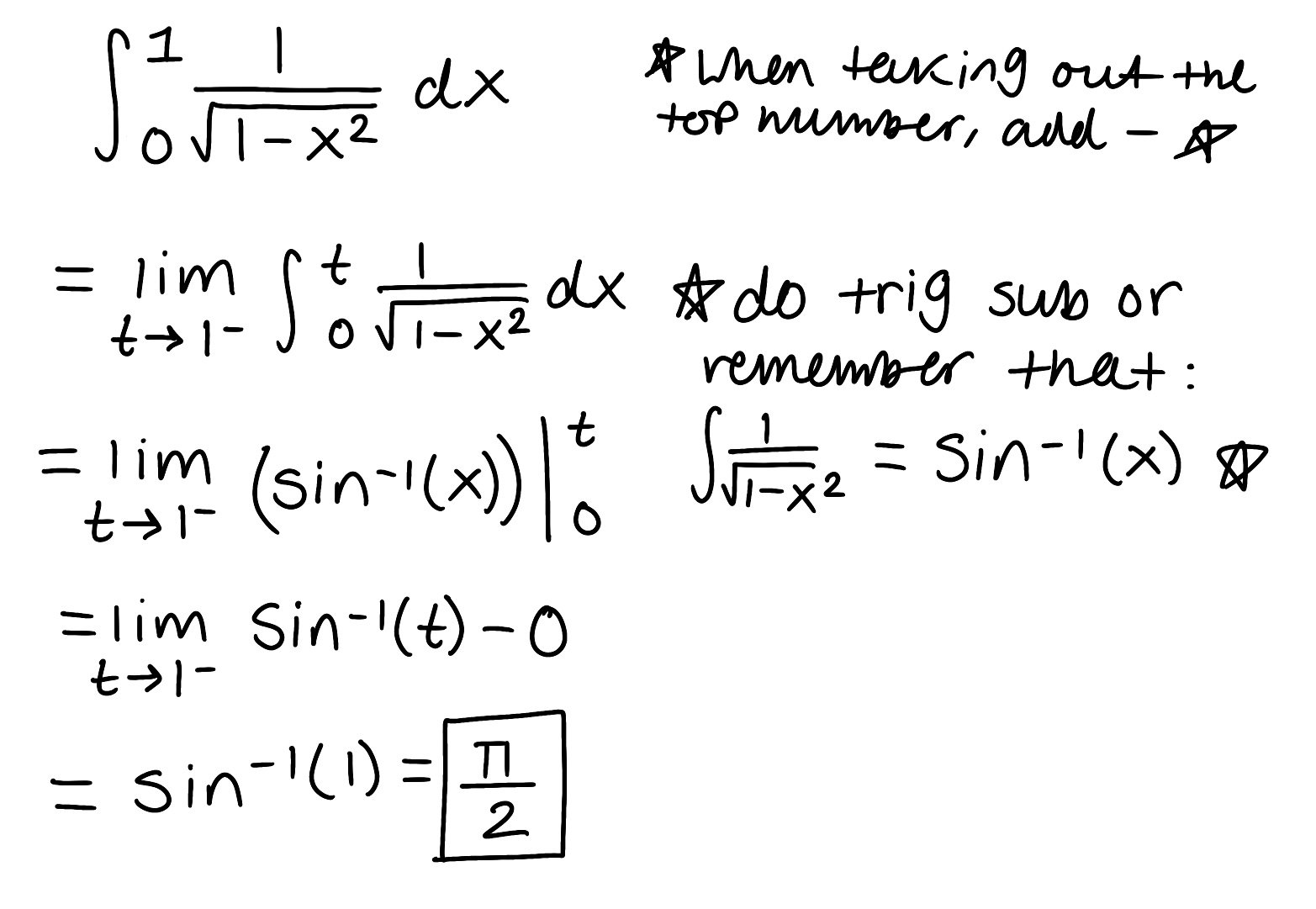
<ul><li><p>The integral is improper because there is a discontinuity x=1 </p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
8
New cards
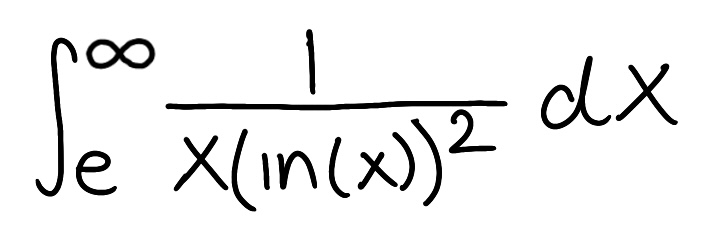
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

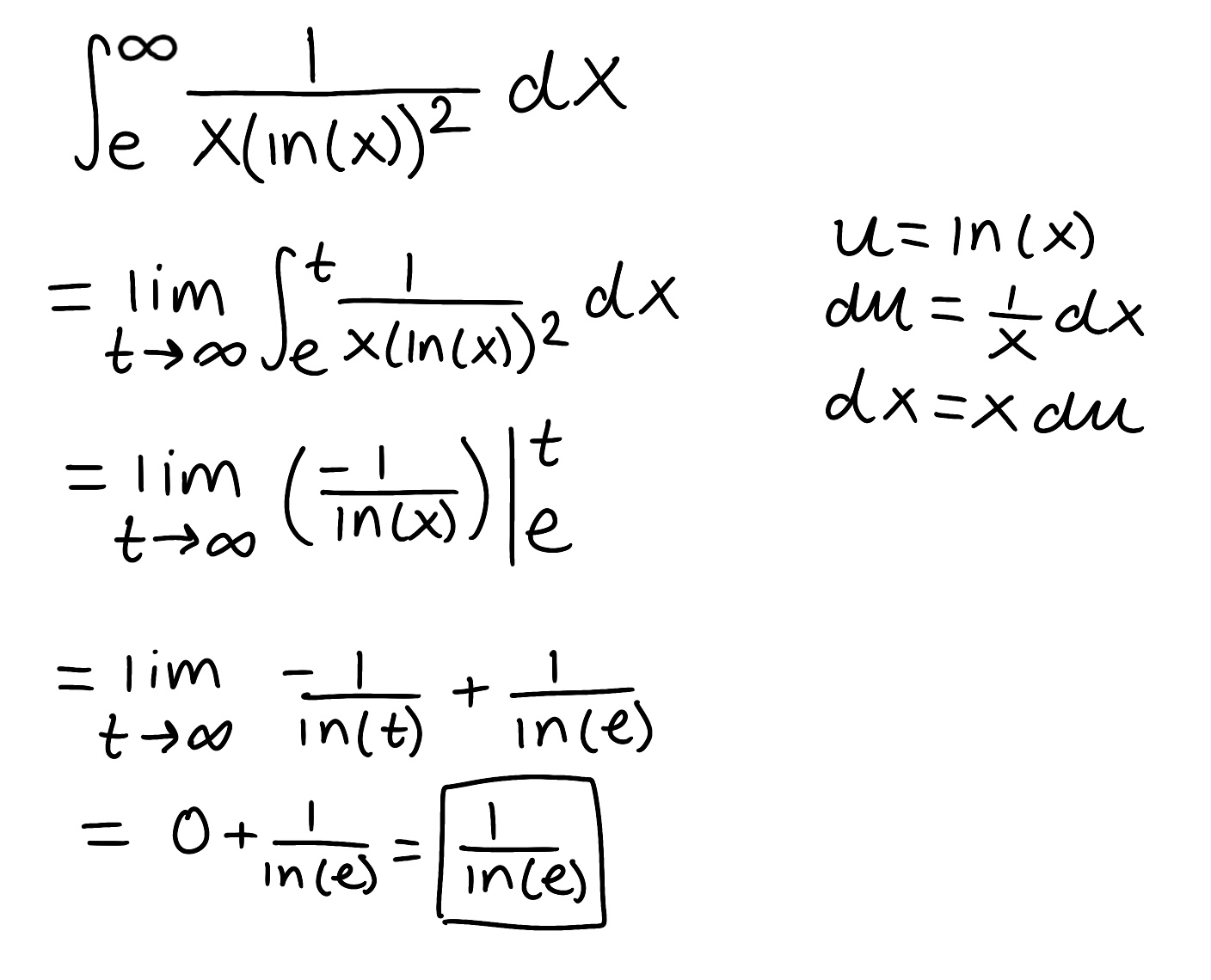
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
9
New cards
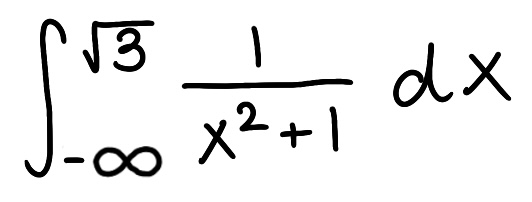
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper</p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

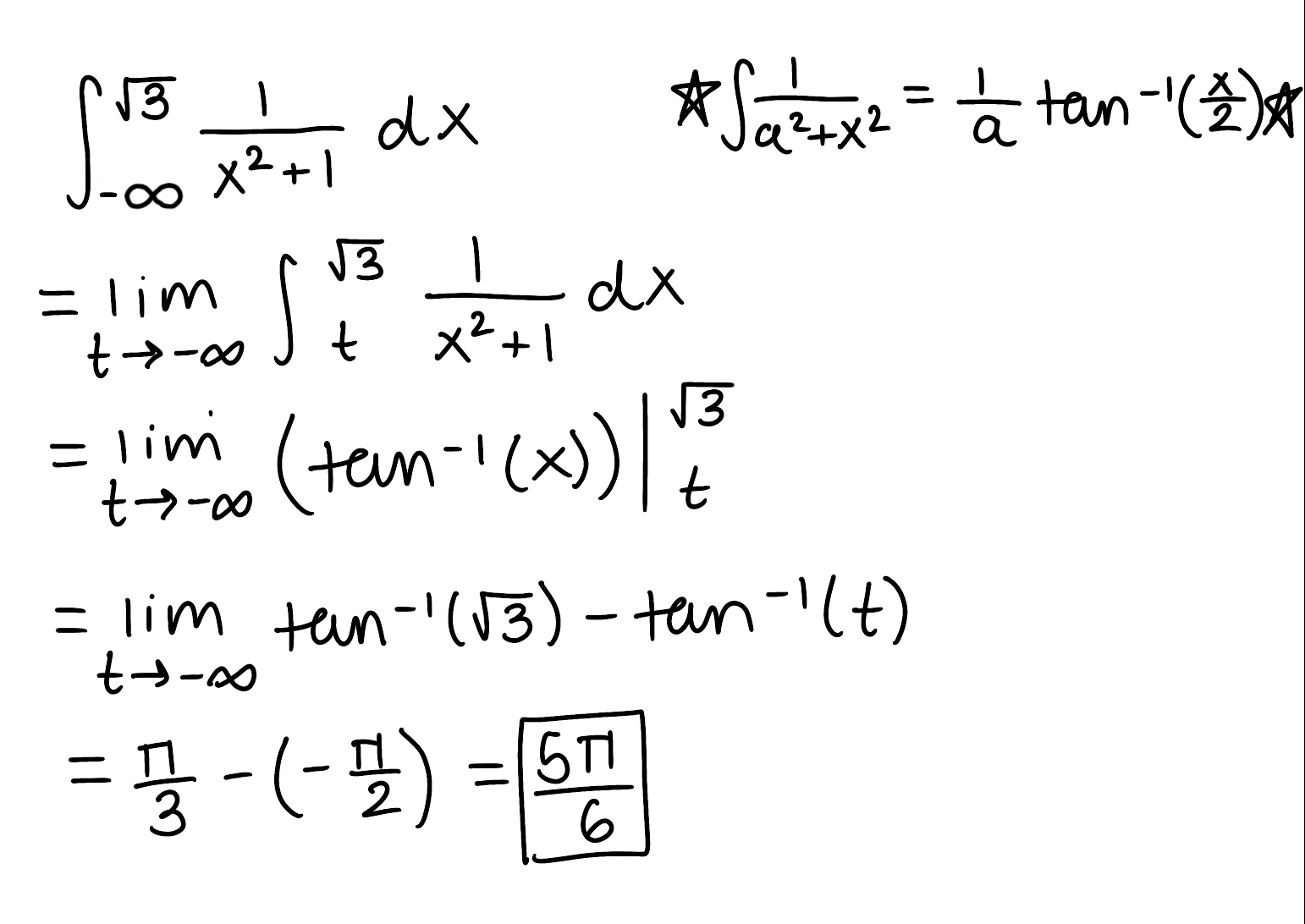
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
10
New cards
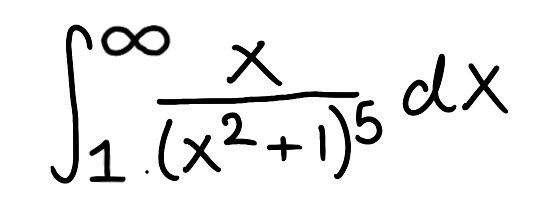
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper </p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because one of the bounds is infinite

  • The integral converges because the limit is finite

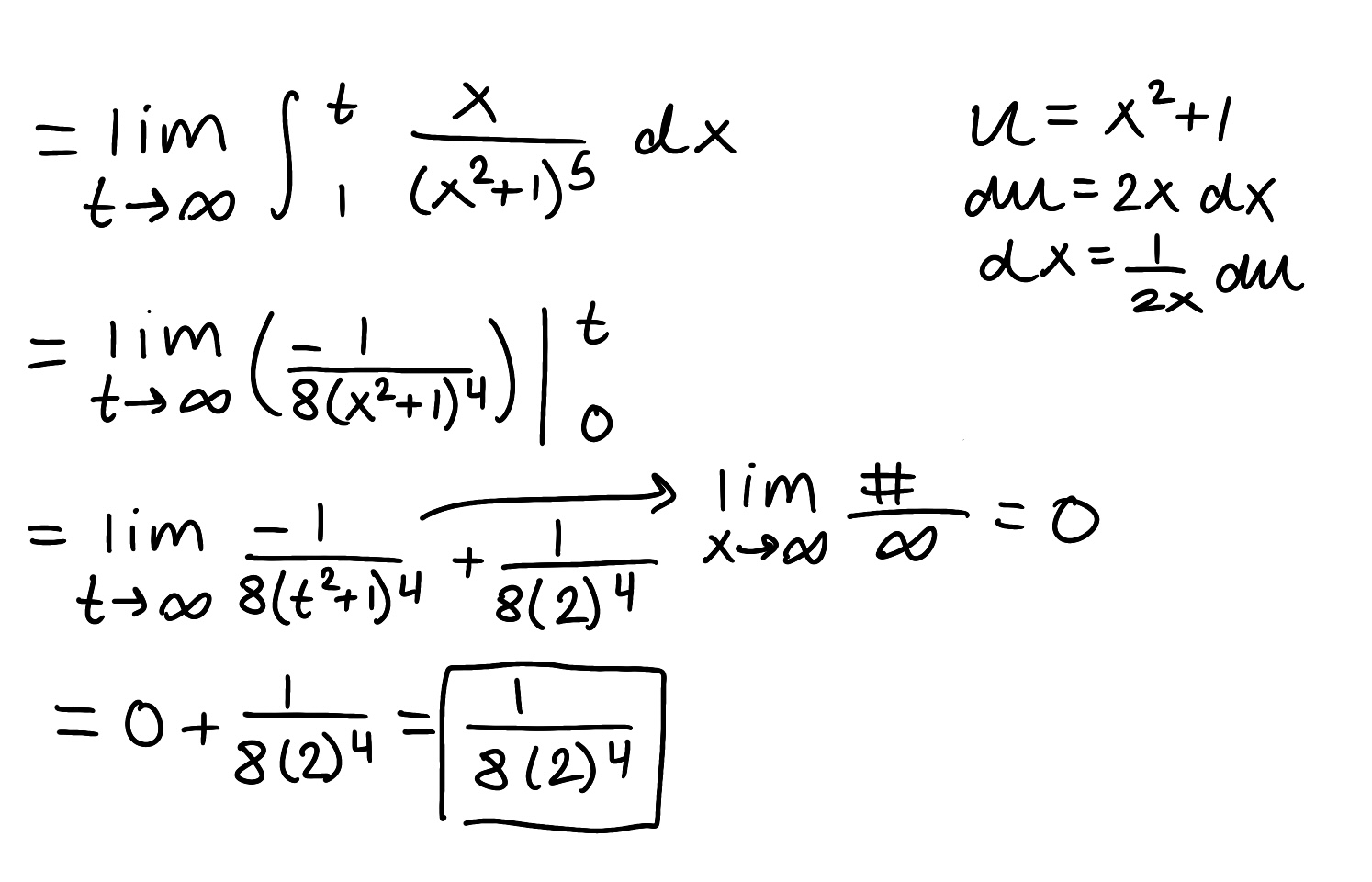
<ul><li><p>The integral is improper because one of the bounds is infinite</p></li><li><p>The integral converges because the limit is finite</p></li></ul><p></p>
11
New cards
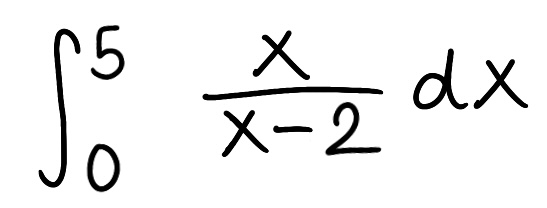
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper</p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because there is a discontinuity at x=2

  • The integral diverges because the limit is infinite

<ul><li><p>The integral is improper because there is a discontinuity at x=2</p></li><li><p>The integral diverges because the limit is infinite</p></li></ul><p></p>
12
New cards
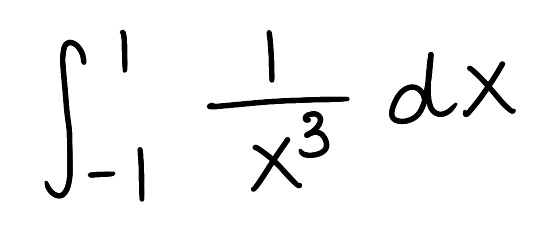
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper</p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because there is a discontinuity at x=0

  • The integral diverges because the limit is infinite

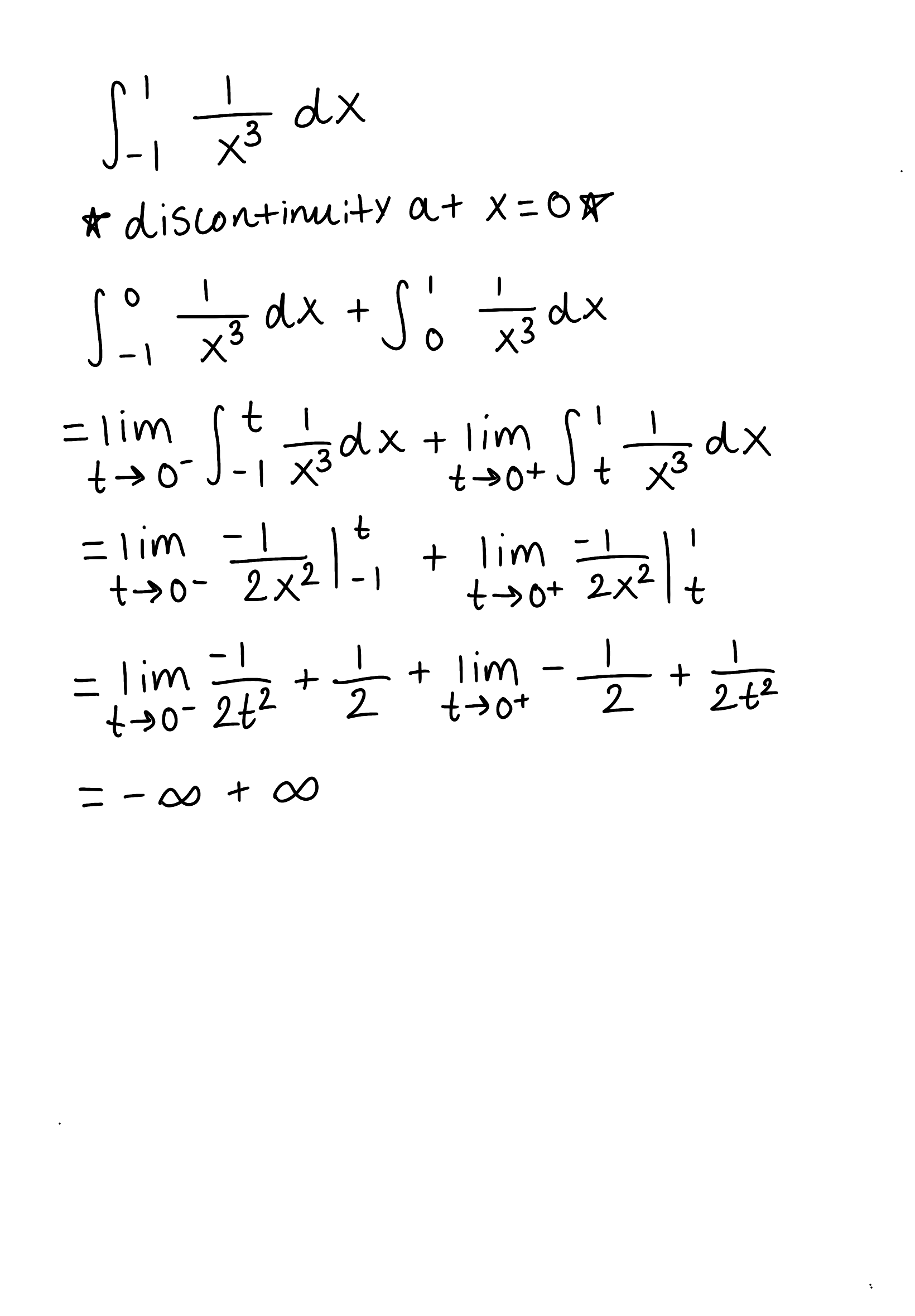
<ul><li><p>The integral is improper because there is a discontinuity at x=0</p></li><li><p>The integral diverges because the limit is infinite</p></li></ul><p></p>
13
New cards
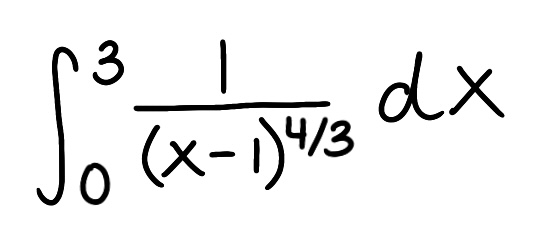
<ul><li><p>Evaluate the integral</p></li><li><p>Explain why the integral is improper</p></li><li><p>Determine if the integral converges or diverges and explain why</p></li></ul><p></p>

  • Evaluate the integral

  • Explain why the integral is improper

  • Determine if the integral converges or diverges and explain why

  • The integral is improper because there is a discontinuity at x=1

  • The integral diverges because the limit is infinite

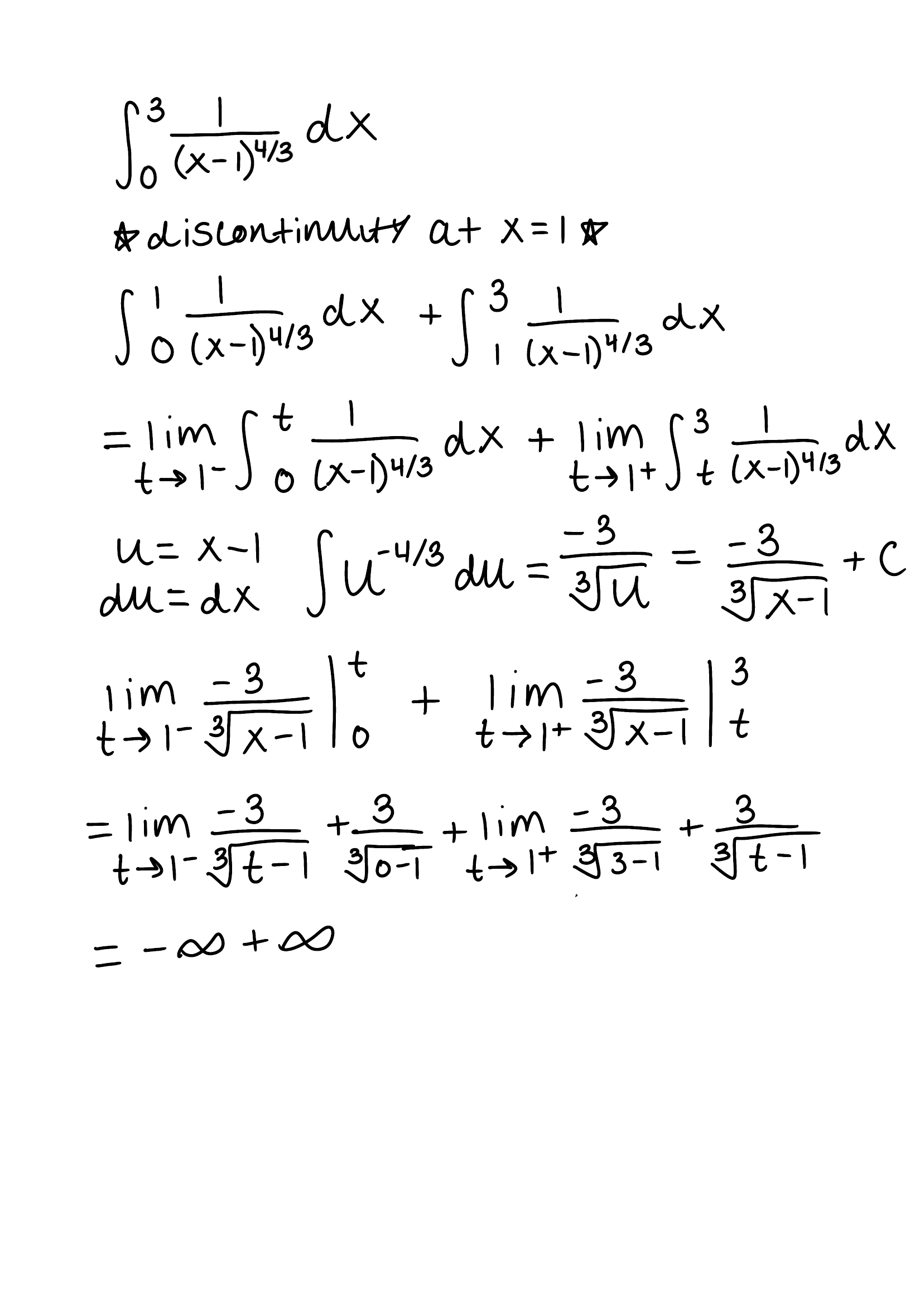
<ul><li><p>The integral is improper because there is a discontinuity at x=1</p></li><li><p>The integral diverges because the limit is infinite</p></li></ul><p></p>
14
New cards

*remember that when when you have to split apart the integral because there is a discontinutiy that is inbetween the bounds, the answer will always be divergent