Multivariable Calculus Lecture 11

Change of Variables in Double Integrals

J is |J|

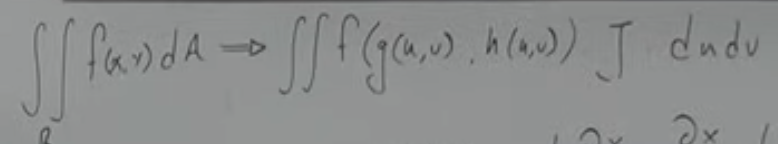
“J” is the Jacobian determinant =

rows = original variables (x,y)

columns = new variables (u,v)

If given transformation from x,y to u,v, plug ___ and ___ into R to get ____ of u and v

Note: get rid of fractions by multiplying to make it easier

Then find ___ and rewrite your double integral in terms of ___

“x=”, “y=”, bounds

|J|, u & v

How to pick your transformation

• parallelogram —> _____

• ellipse —> ___

• in general: _____ w/ ____ = u, other complicated expression w/ x’s and y’s = v

rectangle

circle

complicated expression, x’s and y’s

Transforming a triple integral

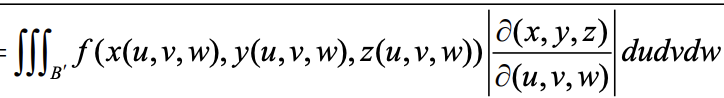
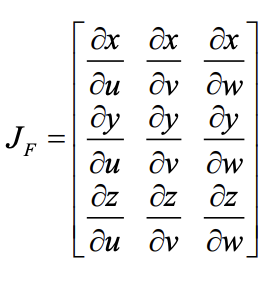
integrals along curve

steps to creating integral equation for curve

1. find r(t) by finding x(t) and y(t)

   1. for circles, x=____ and y=____, therefore bounds of t will be ____

   2. for line segments, we want 0 ≤ t ≤ 1 so x=____ and y=____. Assign one point t=__ and other point t=__, solve for c’s and k’s to get r(t)

   3. for variables in terms of each other (eg. y=x²) make one variable __ and the other in terms of t (y=x² —> x=t, y=t², t bounds would be x coords of the two points of line seg)

2. find ___

3. rewrite integral in terms of t

rcost, rsint, angles

c1 + k1t , c2 + k2t, 0, 1

t

||r’t||

when solving for integral equation for curve,

If you don’t get integral w/ respect to ds, like dx + dy + dz, after solving for ___, do dx = __dt and dy=__dt, replace them in the f(rt) equation and combine, and then don’t need ||r’t||

if C is not smooth…

r(t)

do multiple integrals and add

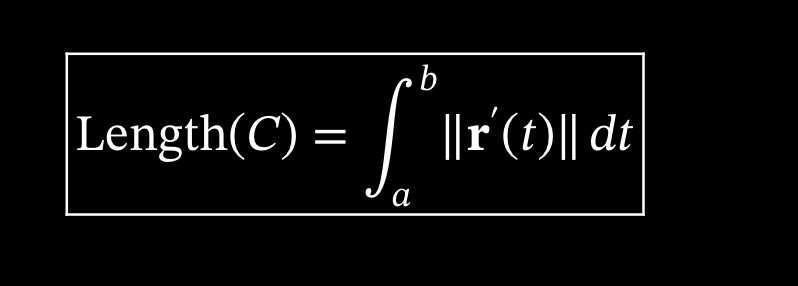
arclength of curve C

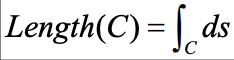
average value of f defined along curve c

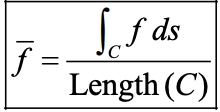
centroid of curve

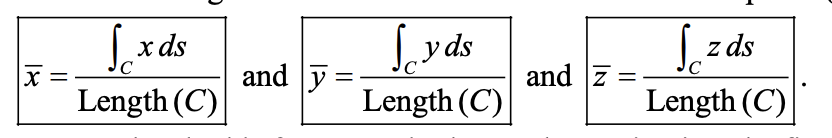
Center of Mass of region C

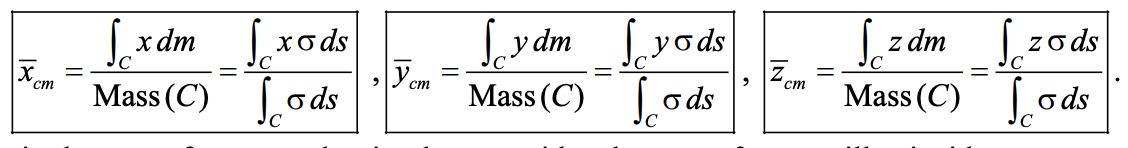
Work done by moving particle along C thru nonconservative vector field

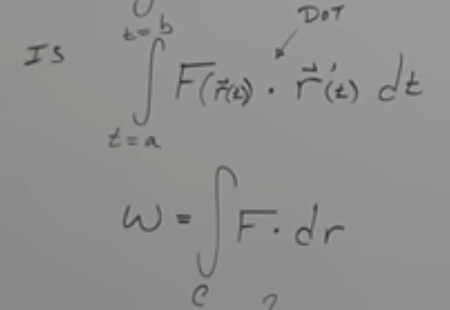
Steps for solving Work done by moving particle along C thru nonconservative vector field

1. reparametrize to get r(t) and t bounds

2. rewrite F(x,y) into ___ and find ___

3. do the ______

4. integrate

F(r(t)), r’t

dot product

Vector Field

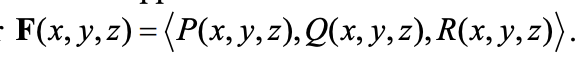
Fundamental Theorem of Line Integrals

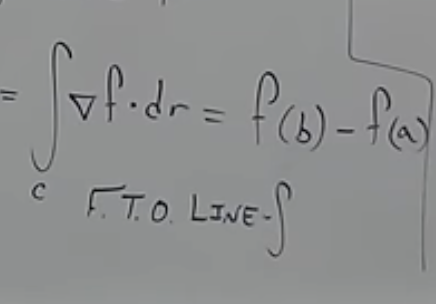
Solving for work Using Fundamental Theorem of Line Integrals

1. Show vector field F is conservative

   1. F(x,y) = 〈P, Q〉—> ______

   2. F(x,y,z) =〈P, Q, R〉 —> Curl F = 0 (every part must be 0) or _____

2. F = ∇f = 〈∂f/∂x, ∂f/∂y, ∂f/∂z〉

   1. _____ = expression + “g(y,z)”

      1. partial derivative w/r/t y and z, if u get ∂f/∂y, ∂f/∂z from earlier just add “c”

   2. derivative of that w/r/t ___ = expression + ∂g/∂y

   3. set equal to ___ —> solve for ∂g/∂y

   4. _____ ∂g/∂y w/r/t y —>____, plug this into “g(y,z)” for f(x,y,z)

   5. derivative of f w/r/t z = expression + “h’(z)”, set equal to ∂f/∂z and solve for h’z

   6. integrate h’(z) w/r/t z = h(z) + c, add to f(x,y,z) for full expression

3. Use fundamental theorem: ____

∂Q/∂x =∂P/∂y

∂Q/∂x =∂P/∂y, ∂R/∂x =∂P/∂z, ∂R/∂y =∂Q/∂z the partials with respect to the other variables must be equal

∫∂f/∂xdx

y

∂f/∂y

integrate

g(y)+”h(z)”

f(x,y)

f(b)-f(a)