6.5 Least Squares Solution

if A is an mxn matrix and B is in R^m then a least squares solution of Ax = b is an x^ in Rⁿ such that:

||b-Ax|| <= ||b-Ax||

for all x in Rⁿ

Ax =

projCol(A)b = b^

Ax^ = b^

x^ is the solution to this

if there are free variables, there might be infinitely many least squares solutions

normal equations for Ax=b are given by

A^TAx = A^Tb

if there are free variables when calculating for x^(sokution for least squares), then there are ? many solutions

infinitely

let A = mxn matrix. the following statements are logically equivalent

a. the equation Ax=b has a unique least squares solution for each b in R^m

b. the columns of A are linearly independent

c. the matrix A^TA is ?

invertible

when the previous statements are true, the least squares solution is

x^ = (AA^T)^-1A^Tb

least squares error of an approximation

||b-Ax^||

the equation Ax=b has a unique least squares solution given by

x^ = R^-1Q^Tb

the least squares solution of Ax=b can also be the weights of the solution of the orthogonal projection of b onto ColA

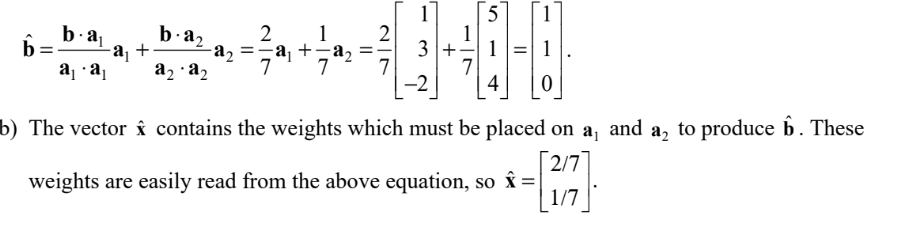
u can be a least squares solution if Au is the ? point in ColA to b

closest (use least squares error formula to check)

T/F) The general least-squares problem is to find an x that makes Ax as close as possible to b.

True

(T/F) If b is in the column space of A, then every solution of Ax=b is a least-squares solution.

true

T/F) A least-squares solution of Ax=b is a vector xˆ that satisfies Axˆ=bˆ, where bˆ is the orthogonal projection of b onto Col A.

true

T/F) A least-squares solution of Ax=b is a vector xˆ such that ∥b−Ax∥≤∥b−Axˆ∥ for all x in ℝn.

False; the inequality points in the worng direction

T/F) Any solution of ATAx=ATb is a least-squares solution of Ax=b.

True

(T/F) If the columns of A are linearly independent, then the equation Ax=b has exactly one least-squares solution.

true

T/F) The least-squares solution of Ax=b is the point in the column space of A closest to b.

false; if x^ is the least squares solution, then Ax^ is the point in the column space of A closest to b

T/F) A least-squares solution of Ax=b is a list of weights that, when applied to the columns of A, produces the orthogonal projection of b onto Col A.

true

(T/F) The normal equations always provide a reliable method for computing least-squares solutions.

false

(T/F) If A has a QR factorization, say A=QR, then the best way to find the least-squares solution of Ax=b is to compute xˆ=R−1QTb

false