APCalculus

IVT

Intermediate Value Theorem

If f is a continuous function on interval [a,b] then for every value M between f(a) & f(b) there’s a value C contained in (a, b) such that f© = M

Corrolary

If f is continuous on [a, b] and if f(a) & f(b) are nonzero w/ opposite signs, then f has a zero in (a, b) w/ a c in [a, b]

Continuity + Rules

Continuous is on an open interval if the graph of f(x) has no breaks, gaps & interruptions

1. f© is defined

2. lim x to c f(x) exists

   1. f© and lim x to c f(x) are the same

types of discontinuities

removable discontinuity

infinite discontinuity

jump discontinuity

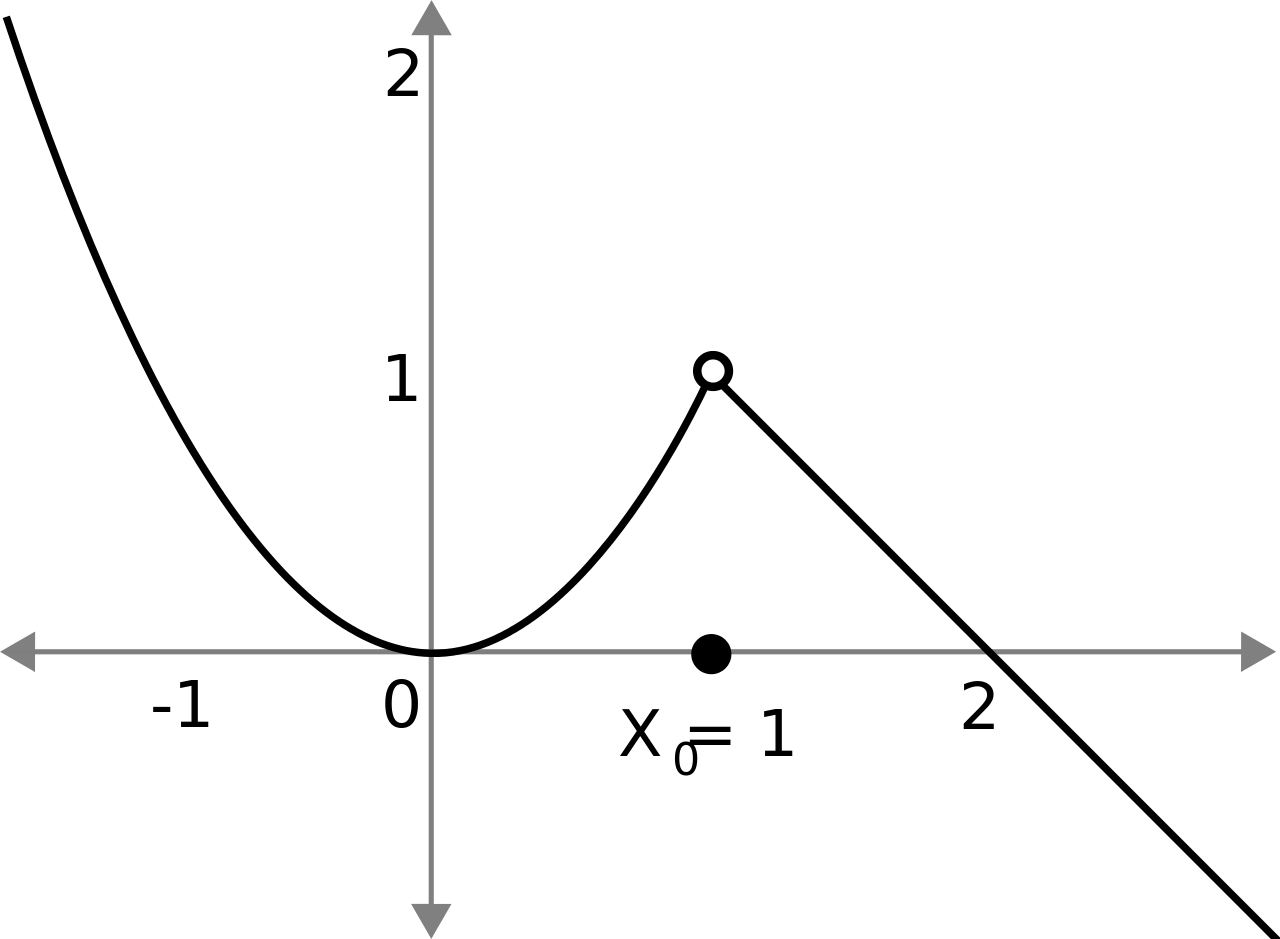
removable discontinuity

when lim x approaching c f(x) exists but isn’t equal to f©.

It’s removable as you redefine f© equal to the limit value.

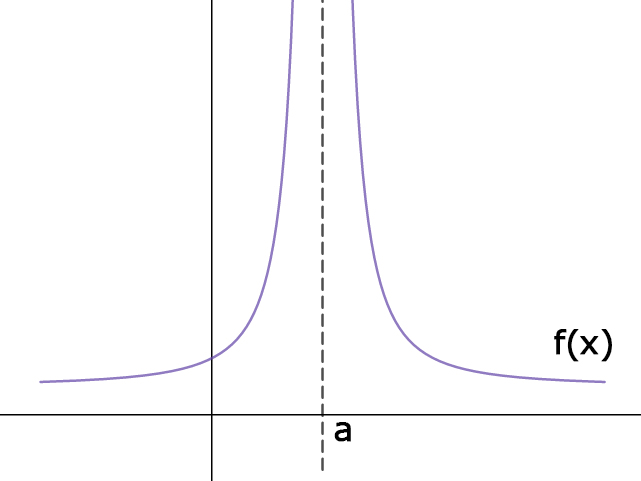
infinite discontinuity

if one/both of the one sided limitsw are infinite, then there’s a infinite disc. it’s non-removable and is when there’s a vertical asymptote.

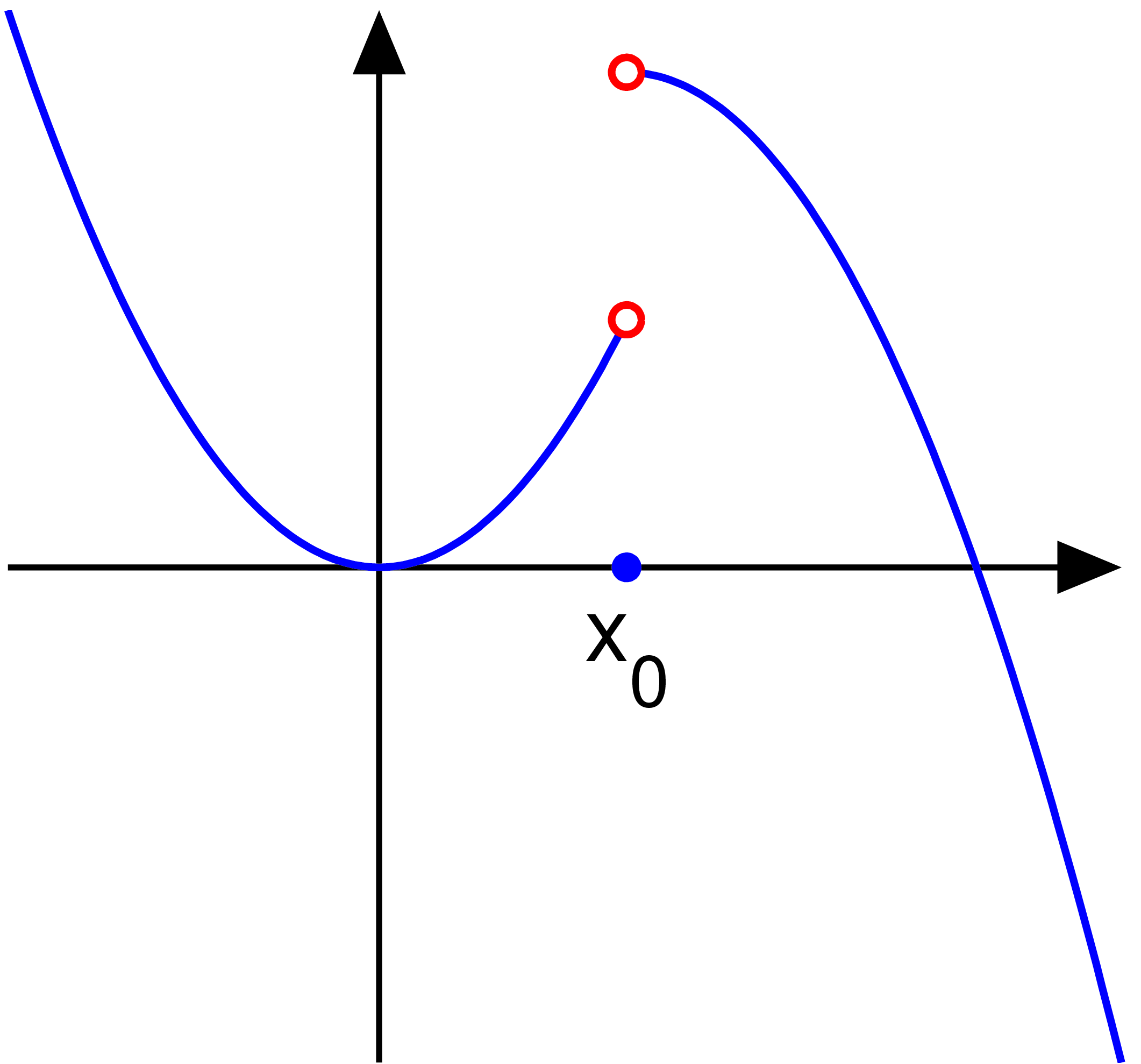
jump discontinuity

if one sided limits of a function approaching diff sides are not equal then it’s a jump discontinuity and non removable.

Squeeze Theorem

if h(x) < f(x) < g(x)

and lim of h(x) and g(x) approaching the same thing is c, f(x) approaching that is also c

Infinite Limits

if degree in n < d = lim is 0

d > n = lim is infinity/-infinity, when it’s equal, divide coeficients

Horizontal Asymptote

top < d, y= 0

d > top = none, slant

equal = divide coefficients

d/dx (sinx)

cos x

d/dx (cos x)

-sin x

d/dx (tan x)

sec² x

d/dx (cot x)

-csc² x

d/dx (sec x)

secxtanx

d/dx (cscx)

-cscxcotx

d/dx (e^u)

u’

d/dx (a^u)

ln a a^u u’

d/dx ln u

u’ / u

d/dx log a u

u’ / ln a * u

tangent line

y - f'(a) = f’(a) (x-a)how

how to solve implicit differentiation

everytime you take derivative of y, replace it with dy/dx.

how to know if a function has a inverse function

if it passes horizotal line test, one to one, and strictly incr/decr

slopes of inverse functions

reciprocal

d/dx (arcsin u)

u’/(sqrt(1-u²))

d/dx (arccos u)

-u’/(sqrt(1-u²)

d/dx (arctan u)

u’/1+u²

d/dx (arccot u)

-u’/(1+u²)

d/dx (arcsec u)

u’/(|u| sqrt(u² - 1)

d/dx (arcsc u)

-u’ / (|u| sqrt(u² - 1))