AP Statistics CH 5 Summarizing Bivariate Data

bivariate data

data with 2 variables; shown using a scatterplot

describe a scatterplot using DUFS

D - direction (+/-)
U - unusual occurrences
F - form (linear/nonlinear)
S - strength (strong/moderate/weak)

correlation coefficient (r)

measures the strength of any linear relationship
0.8 < r < 1 = strong
0.5 < r < 0.8 = moderate
0 < r < 0.5= weak

- has the same sign as the slope (b)
- switching x and y does not matter
- not resistant to outliers
- cannot imply causation, only association/correlation

least-squares regression line

ŷ = a + bx
a = average/mean of y when x=0
b = slope; for every 1 unit increase y increases by ___

- describes the linear relationship between the explanatory and response variable
- goal is to minimize residuals
- always passes through (x̄ , ȳ)

creating a LSRL without data

b = r(Sy/Sx)
ȳ = a + bx̄
ŷ = a + bx

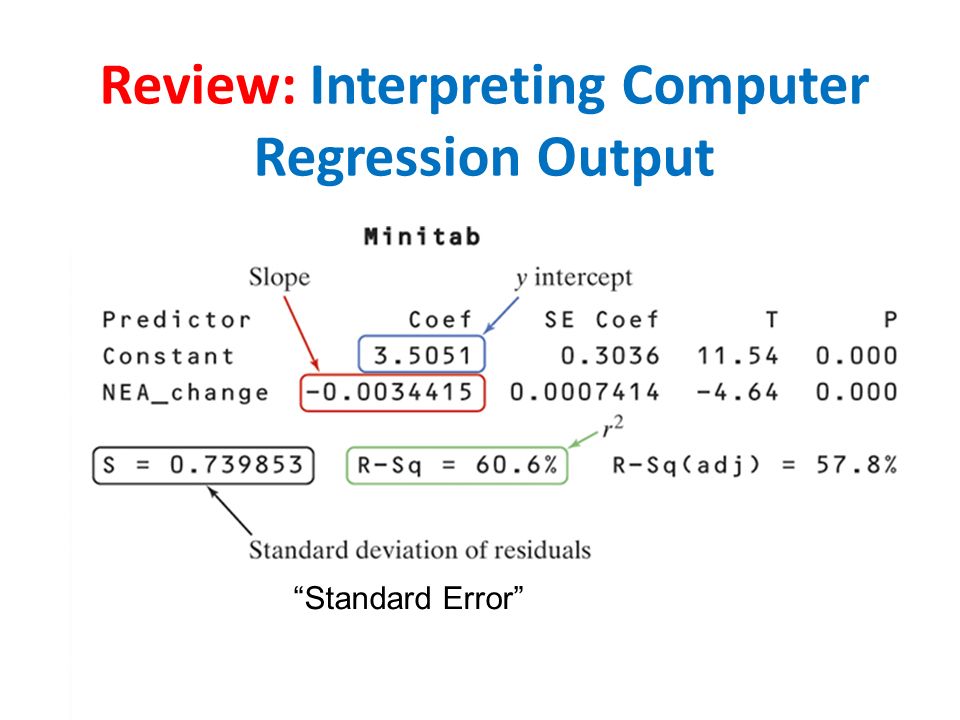
minitab outputs

a = y-intercept
b = slope
s = standard deviation
R-sq = r^2

extrapolation

- prediction outside the range of x-values
- we cannot assume the linear pattern continues forever outside the range

residual

y - ŷ
observed y - predicted y

- error between the predicted LSRL value and the actual data value

residual predictions

- over-prediction: negative residual
- under-prediction: positive residual

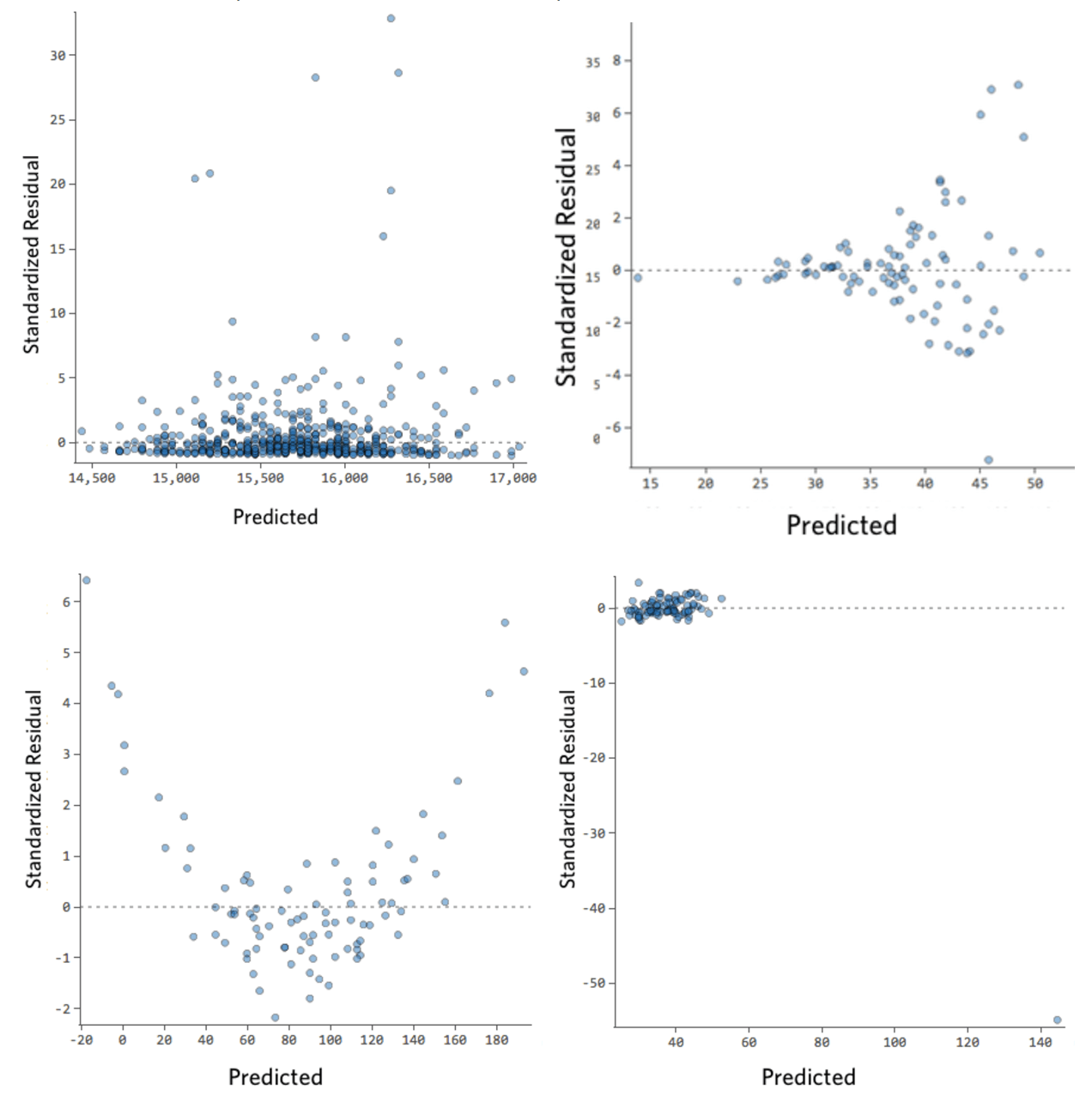
residual plots

- shows whether a linear plot is good for data
- plot (x , residual)
- a GOOD residual plot has random scatter
- a BAD residual plot is curved, fanning or isolated points

influential points

- points that fall far below/above the horizontal line
- x-value varies significantly from the others
- heavy influence on the LSRL
- a significant change in slope indicates influential point

delete the value and recalculate the LSRL to determine if it is influential

coefficient of determination (r^2)

- the proportion of variability in y that can be attributed to an approximate relationship between x and y
- how much of y is explained by x?

"___% of the variability in [y] can be explained by [x]."

standard deviation of residuals (s)

- the typical error between data points and the LSRL
strong correlation = low standard deviation
weak correlation = high standard deviation

"The typical amount of variability from the observed [y] to the regression line is [s]."

exponential model

original: y = ab^x
transformed: lnŷ = a + bx or logŷ = a + bx

- only change either x or y

power model

original: y = ab^x
transformed: lnŷ = a + b(lnx) or logŷ = a + b(logx)

- change both x and y