Clustering

What is clustering?

Cluster analysis is a technique used to group similar data points based on their characteristics.

It helps:

• Visualising high dimensional data

• Structuring data

• Classification

How does clustering relate to EDA?

Cluster analysis is a key EDA tool because it:

1. Shows hidden patterns within data

2. Reveals structure in high-dimensional datasets that are otherwise hard to visualize

3. Generates hypotheses by identifying meaningful segments (e.g., customer types)

4. Reduces data complexity by summarizing observations into clusters

5. Supports visualization, such as dendrograms or scatter plots with clusters colored distinctly

Main limitation of clustering

• Different ways to measure distance between points which changes which points are grouped together  

• Using different clustering methods gives different groups

• Sometimes clusters don’t match real/meaningful groups in data

• There’s no correct way to form clusters

Types of clustering

1. Hierarchical clustering

2. K-means clustering

What is hierarchical clustering, and what are its two main approaches?

Hierarchical clustering builds a tree (hierarchy) of clusters.

Two main approaches:

1. Agglomerative (bottom-up):

   Start with each point alone, then keep merging the closest clusters until there’s only one big cluster.

2. Divisive (top-down):

   Start with all points in one cluster, then keep splitting into smaller clusters step by step.

Distance measures used in clustering

1. Euclidean distance

   Straight-line distance between two points, like drawing a line between them. Good for simple number data.

2. Manhattan distance:

   Add steps you’d take along a grid

3. Cosine Similarity:

   Looks at the angle between two data points

Linkage methods in Hierarchical clustering

Decide how we measure the distance between clusters when we merge them.

Methods:

1. Single linkage

2. Complete linkage

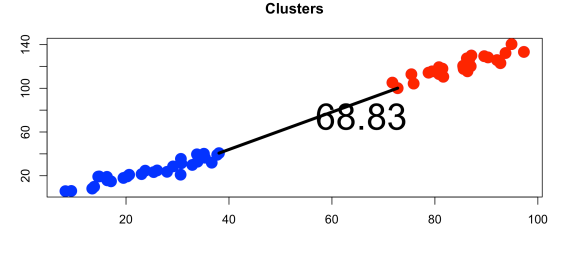
Single Linkage

Use the closest points between two clusters → can create long, chain-like clusters

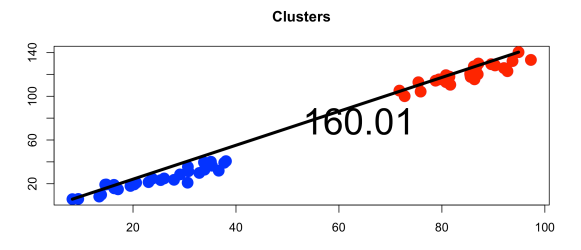
Complete Linkage

Use furthest points between 2 clusters → makes tighter, rounder clusters

Agglomerate (bottom-up) Clustering Method Steps:

1. Treat each observation as its own cluster

2. Measure distances between each observation (each cluster) using a distance metric (eg. Euclidean)

3. Find 2 closest clusters and merge them

4. Recalculate distances between clusters using single or complete linkage

5. Repeat steps 2-4 until only 1 cluster remains

Advantages vs Disadvantages of hierarchical clustering

Advantages:

1. don’t need to choose number of clusters before starting

2. produces dendogram which shows order in which clusters were merged

3. Great for small-medium datasets

Disadvantages:

1. Slow for large datasets

2. Sensitive to outliers and messy data

3. Once clusters are merged they can’t be split

Dendogram

Tree diagram that shows how data points were grouped in hierarchical clustering

How to read:

1. X-axis:

   • Shows data points (observations before clustering)

2. Y-axis:

   • Shows how far apart clusters were when combines

   • Height of each horizontal line (called a “merge”) shows distance between clusters

     Low line = Very similar

     High line = Less similar

3. What does long horizontal line mean:

   • Shows a big jump in distance (2 very different clusters merged)

   • Helps spot clear breaks in data where you can cut the tree

4. How to choose number of clusters

   • Cut the tree horizontally at a height where there’s a stable number of clusters (a small change in height won’t change the number of clusters) -→ look for long horizontal lines

   • Wherever the cut crosses vertical lines tell you how many clusters you’ll get

Choosing number of clusters

• No one correct answer

• Too few clusters makes clustering pointless

• Too many clusters may be hard to interpret or use

Non-hierarchical clustering

• Used when exact number of clusters is known

• Example: k-means clustering

K-means Clustering Optimising Clusters

• In clusters (k groups), each point is closest to its own cluster’s mean (centroid)

• A point cant be closer to the mean of a different cluster

• Minimises sum of squares within cluster (tries to keep points in a cluster as close to the centroid as possible

Steps of k-means clustering

1. Pick how many clusters (K) you want.

2. Choose starting points (centroids) for each cluster (often randomly).

3. Put each data point into the closest group (based on distance).

4. Move each centroid to the average location of the points in the cluster.

5. Repeat steps 3–4 until there’s minimal change

Algorithms for solutions to k-mean

These alogirthms are used because k-means is a NP-hard problem

There’s no quick way to guarantee finding the best clustering

Instead of trying all combinations we use the following heuristics:

• Lloyd’s Algorithm

• Hartigan-Wong theorem

Lloyd’s Algorithm

1. Pick starting centroids (often random)

2. Put each point in a cluster with the closest centroid

3. Move each centroid to the mean of all observations in the cluster

4. Repeat steps 2-3 until there’s no more change

Label Switching in k-means clustering

Cluster labels (eg.1,2,3) are arbitrary and can change. The labels don’t metter

Outputs from the kmeans() function in R?

• cluster: A vector showing the cluster assignment of each data point

• centers: Coordinates of the centroids (mean values of variables) of each cluster

• size: Number of observations in each cluster

Why is comparing cluster solutions difficult?

• There’s no correct answer

• Different methods of clustering give different results

Robustness

• Means cluster solutions stay consistent even if algorithm changes

Check robustness by:

1. Compare results from different methods

2. Use Rand Index(RI) or Adjusted Rand Index(ARI)

Rand Index

Measures how similar cluster groupings using 2 different methods are

0=no agreement

1= perfect agreement

Adjusted Rand Index

Improves rand index by adjusting for agreement that might happen due to chance

0=no agreement

1=perfect agreement

Advantages + disadvantages k-means clustering

Advantages:

• Fast when there is a large number of observations

• the number of clusters is known

• when there is no obvious hierarchy in the data

Disadvantages:

• Must choose number of clusters at the start and its not always obvious

• Random starting centroids give different result every time

• Doesn’t always find best solution (depends on starting centroids)